Table of Contents
Syntax analysis or parsing is about discovering structure in text and is used to determine whether or not a text conforms to an expected format. "Is this a textually correct Java program?" or "Is this bibliographic entry textually correct?" are typical questions that can be answered by syntax analysis. We are mostly interested in syntax analysis to determine that the source code of a program is correct and to convert it into a more structured representation (parse tree) for further processing like semantic analysis or transformation.
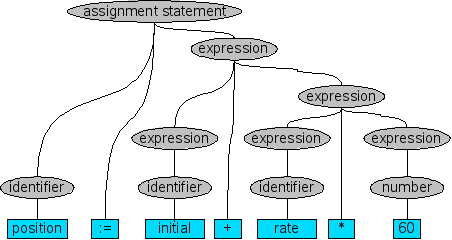
Consider the following text fragment from a program (this example is taken from [ASU86]):
position := initial + rate * 60
How can we determine that this is a correct assignment statement?
First of all, this is a sequence of individual characters
p, o , s, and so
on. This is shown in Figure 1.1, “Text of example”.
It makes sense to first group these character as follows:
-
The identifier
position. -
The assignment symbol :=.
-
The identifier
initial. -
The plus sign.
-
The identifier
rate. -
Th multiplication sign.
-
The number
60.
This process of grouping individual characters is called lexical analysis or lexical scanning, the result is shown in Figure 1.2, “Lexical analysis of example”. Observe that the spaces have disappeared and are left unclassified (we will come back to this in the section called “Lexical versus context-free grammar”).
Next, we want to determine that this is a structurally correct
statement. This is the main province of syntax analysis or parsing as it
is usually called. The result of parsing is a parse
tree as shown in Figure 1.3, “Parse tree of example”. This parse tree reflects the
usual meaning of arithmetic operators: since multiplication is done before
addition, the sub phrase rate * 60 is grouped together
as a logical unit.
The hierarchical structure of programs is usually described by recursive rules like the following ones that describe expressions:
-
Any Identifier is an expression.
-
Any Number is an expression.
-
If Expression1 and Expression2 are expressions, then so are:
-
Expression1
+Expression2 -
Expression1
*Expression2 -
(Expression1)
-
According to rule (1) position,
initial and rate are expressions.
Rule (2) states that 60 in an expression. Rule (3) says
that rate * 60 is an expression and finally that
initial + rate * 60 is an expression. In a similar
fashion, language statements can be defined by rules like:
-
If Identifier1 is an identifier and Expression2 is an expression, then
-
Identifier1 := Expression2
is a statement.
-
-
If Expression1 is an expression and Statement2 is a statement, then
-
while (Expression1) doStatement2 -
if (Expression1) thenStatement2
are statements.
-
These rules are called grammar rules and a collection of such rules is called a context-free grammar or grammar for short.
We will now discuss the basic concepts that are vital for understanding syntax analysis. While doing so, we will use examples written in SDF (see ????), the Syntax Definition Formalism used in The Meta-Environment (see, http://www.meta-environment.org)
At the lowest level, the lexical notions of a language like identifiers, keywords, and numbers have to be defined in one way of another. The same holds for the layout symbols (or whitespace) that may surround the lexical tokens of a language. The common understanding is that layout symbols may occur anywhere between lexical tokens and have no further meaning. Let's get the boring stuff out of the way, and let's define the lexical syntax of our example:
[ \t\n]* -> LAYOUT [a-z][A-zA-Z0-9]* -> Identifier [0-9]+ -> Number
The left-hand side of these rules describes the pattern of interest and the right-hand side defines the name of the corresponding lexical category. In all these left-hand sides two important notions occur:
-
Character classes like
[0-9]that describes the characters from0to9. -
The repetition operators
*(zero or more) and+(one or more).
The first rule states that all spaces, tabulation or newline
characters are to be considered as layout. The second rules states that
identifiers start with a lowercase letter and may be followed by zero or
more letters (both cases) and digits. The last rule states that a number
consists of one or more digits. Note that we have not yet said anything
about other lexical tokens that may occur in our example statement, like
:=, + and * and
parentheses.
It is time to move on to the definition of the structure of our example language. Let's start with the expressions:
Identifier -> Expression
Number -> Expression
Expression "+" Expression -> Expression
Expression "*" Expression -> Expression
"(" Expression ")" -> Expression
Not surprisingly, we follow the rules as we have seen above. Observe, that these rules contain literal texts (indicated by double quotes) and these are implicitly defined as lexical tokens of the language. If you are worried about the priorities of addition and multiplication, see the section called “Disambiguation methods” below.
The final step is to define the structure of the assignment statement:
Identifier ":=" Expression -> Statement
For completeness, we also give the rules for the while and if statement shown earlier:
"while" "(" Expression ")" "do" Statement -> Statement
"if" "(" Expression ")" Statement -> Statement
Traditionally, a strict distinction is being made between lexical syntax and context-free syntax. This distinction is strict but also rather arbitrary and is usually based on the implementation techniques that are being employed for the lexical scanner and the parser. In The Meta-Environment we abolish this distinction and consider everything as parsing. Not surprisingly our parsing method is therefore called scannerless parsing.
The careful reader will observe that we have skipped over an important issue. Consider the expression:
1 + 2 * 3
Should this be interpreted as
(1 + 2) * 3
or rather as
1 + (2 * 3).
The latter is more likely, given the rules of arithmetic that prescribe that multiplication has to be done before addition. The grammar we have presented so far is ambiguous, since for some input texts more than one structure is possible. In such cases, disambiguation rules (priorities) are needed to solve the problem:
context-free priorities Expression "*" Expression -> Expression > Expression "+" Expression -> Expression
Other disambiguation mechanisms include defining left- or right-associativity of operators, preferring certain rules over others, and rejection of certain parses.
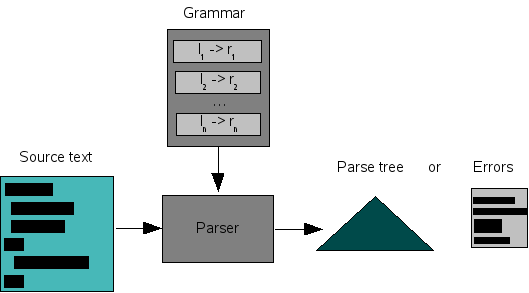
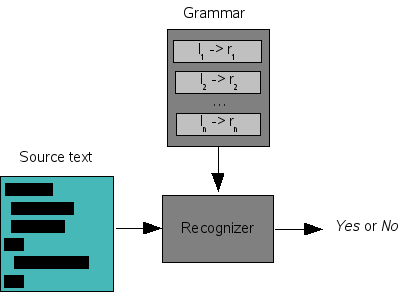
In its simplest form, syntax analysis amounts to recognizing that a source text adheres to the rules of a given grammar. This is shown in Figure 1.4, “A recognizer”. Given a grammar, it takes a source text as input and generates Yes or No as answer. Yes, when the source text can be parsed according to the grammar, and No, when this is not the case. In practice, a recognizer becomes infinitely more useful if it also generates error messages that explain the negative outcome.
Figure 1.4. A recognizer
Pure recognizers are seldomly used, since the parse tree corresponding to the source text is needed for nearly all further processing such as checking or compiling. The more standard situation is shown in Figure 1.5, “A parser”. Given a grammar, a parser takes a source text as input and generates as answer either a parse tree or a list of error messages.
Syntax analysis is one of the very mature areas of language theory and many methods have been proposed to implement parsers. Giving even a brief overview of these techniques is beyond the scope of this paper, but see the references in the section called “Further reading”. In the Meta-Environment we use a parsing method called Scannerless Generalized Left-to-Right parsing or SGLR for short. The least we can do, is explain what this method is about.
We have already encountered the notion of scannerless parsing in the section called “Introduction”. It amounts to eliminating the classic distinction between the scanner (that groups characters into lexical tokens) and the parser (that determines the global structure). The advantage of this approach is that more interplay between the character level and the structure level is possible. This is particularly true in combination with the "generalized" property of SGLR.
The most intuitive way of parsing is predicting what you expect to see in the source text and checking that the prediction is right. Complicated predictions ("I want to parse a program") are split into a number of subsidiary predictions ("I want to parse declarations followed by statements"). This continues until the lexical level is reached and we can actually check that the lexical tokens that occur in the text agree with the predictions. This predictive or top-down parsing takes an helicopter view: you know what you are looking for and check that it is there. This intuitive parsing method has a major disadvantage: for certain grammars the top-down parser will make endless predictions and will thus not terminate.
Left-to-Right or LR indicates a specific style of parsing that is more powerful: bottom-up parsing. Bottom-up parsing is like walking in the forest during a foggy day. You have only limited sight and step by step you find your way. A bottom-up parser considers consecutive lexical token and tries to combine them into higher level notions like expressions, statements and the like. LR parsers can parse more languages than top-down parsers can. However, when combining the pieces together, an LR parser can only work when there is precisely one way to combine them and has to give up otherwise. This means that there are still languages that cannot be parsed by an LR parser.
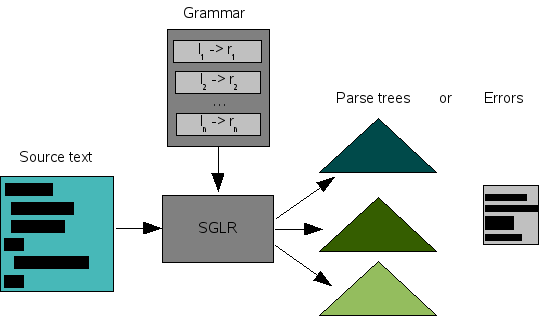
Here comes the generalized in SGLR to the rescue: this removes the restriction that there is only one way to combine recognized parts. In doing so, it becomes possible that not one but several parse trees are the result of parsing. The bonus is that all context-free languages can be parsed by the SGLR parsing algorithm. Figure 1.6, “An SGLR parser” summarizes the use of an SGLR parser. Using SGLR has three key advantages:
-
SGLR recognizes the largest possible class of grammars: all context-free grammars.
-
Context-free grammars can be combined to form another context-free grammar. This enables modular grammars.
-
The integration of lexical scanning and context-free parsing gives more control to the grammar writer to finetune his grammars.
There are many extensions to the grammar descriptions we have seen so far. We single out lists, disambiguation methods and modular grammar for further clarification.
Repeated items are pervasive in programming language grammars: lists of declarations, lists of statements, lists of parameters are very common. Many grammar notations provide support for them. Here is the list notation used in SDF. If we want to define a list of statements, we could write the following:
Statement -> Statements Statement ";" Statements -> Statements
This is a clear description of statements lists, but a shorter description is possible:
{ Statement ";" }+ -> Statements
The pattern defines a list of elements some syntactic category
(e.g., Statement), separated by a lexical token
(e.g., ";"), and consists of one or more (indicated
the +) elements. In a similar fashion lists of zero
or more elements can be defined (using a * instead of
a +). The advantage of the list notation is twofold:
the grammar becomes more compact and the matching of these rules in the
equations becomes more easy.
Many mechanisms exist to disambiguate a given grammar. We mention a few:
-
Priorities. When there is a choice, prefer rules with a higher priority. As a result, rules with a higher priority "bind more strongly". This is, for example, the case when defining the priorities of arithmetic operators.
-
Associativity. In some cases, syntax rules can overlap with themselves. Is
1 + 2 + 3to be parsed as(1 + 2) + 3or rather as1 + (2 + 3)? In the former case, the plus operator is said to be left-associative, in the latter case it is called right-associative. In some cases, an operator is non-associative and the expression has to be disambiguated explicitly by placing parentheses. -
Follow restrictions. Forbid that certain constructs follow each other. Typical example: forbid that an identifier is followed by letters or digits. In this way we can ensure that all possible characters are part of the identifier. In other words, we enforce the longest possible match for all characters that may belong to the identifier.
-
Prefer.
-
Reject. Reject a parse in which a certain grammar rule occurs. For instance, a text like
whilemay be a keyword or an identifier. By rejecting the parse withwhileas identifier we enforce thatwhileis only used as keyword. This is usual in most languages but not in all (e.g., PL/I).
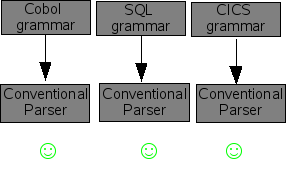
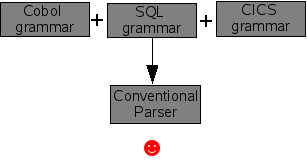
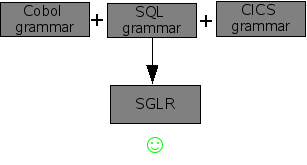
As we have seen in the section called “Parsing methods”, using an SGLR parser enables the creation of modular grammars. This is more exciting than it sounds. Consider, a huge language like Cobol (yes it is still widely used!). In addition to the Cobol language itself there are many extensions that are embedded in Cobol programs: CICS supervisor calls, SQL queries, and the like. Each of these grammars works well if we use them with a conventional parser (see Figure 1.7, “Conventional parser works well with independent grammars”). However, if we attempt to combine the three grammars in ordere\ to be able to parse Cobol programs with embedded CICS and SQL, then disaster strikes. Most conventional parsers will complain about the interference between the three grammars and just refuse to work (see Figure 1.8, “Conventional parser does not work with combined grammars”). For the technically inclined: shift-reduce conflict galore! However, if we try the same with an SGLR parser things go smoothly (see Figure 1.9, “SGLR works well with combined grammars”).
Syntax analysis plays a prominent role in The meta-Environment:
-
To parse source text. Given a grammar for some language (say Java) and a program in that language (a Java program) we can parse the program and obtain its parse tree. This is an example of the approach sketched in Figure 1.6, “An SGLR parser”. This parse tree can then be further processed by applying rewrite rules (equations) defined in an ASF+SDF specification.
-
To parse equations. The equations in ASF+SDF specifications can use the grammar rules that are defined in the SDF part of the specification. The equations have to be parsed first according to that grammar and then they can be used for rewriting.
-
The classical work on grammars in natural languages is [Cho56].
-
Another monumental work on grammars in computer science is the first volume of the two volume series [AU73].
-
A more recent overview of parsing techniques is given in [GJ90]. A second edition is in preparation and will be published by Springer in 2007.
-
On www.meta-environment.org you can find several articles related to SDF.