Table of Contents
- An Introduction to SDF
- The life-cycle of an SDF definition
- Modules
- Comments
- Symbols
- Grammars
- Disambiguation
- Examples
- A simple lexical syntax
- Using Character Classes
- A simple Drawing Language
- Identifiers
- Numbers
- Strings
- Identifier Lists
- An Expression Language with Chain Rules
- Using Labels in Productions
- Groups of Associative Productions
- Associative Productions
- Parameterization
- Symbol Renaming
- Examples on dealing with lexical ambiguity using restrictions
- Some Tricky Cases
- Well-formedness
- Derivations
- Historical Notes
- Bibliography
- To Do
Warning
This document was recently rewritten (May 11th 2007). It is
up-to-date with the latest version of SDF. References to ASF+SDF syntax
and semantics have been removed and descriptions of syntax and semantics
of SDF have been brought up-to-date with the current state. Please contact
<meta-devel-list@cwi.nl> if you would like to contribute to
this document.
If you want to:
-
describe the syntax of an existing language like C, C++, Java, or Cobol,
-
describe an embedded language and need to combine several language grammars,
-
describe the syntax of your newly designed domain-specific language,
-
get a front-end for the semantic analysis of programming or application languages,
then SDF may be the right technology to use.
The Syntax Definition Formalism SDF is intended for the high-level description of grammars for programming languages, application languages, domain-specific languages, data formats and other computer-based formal languages. The primary goal of any SDF definition is the description of syntax. The secondary goal is to generate a working parser from this definition. A parser is a tool that takes a string that represents a program as input and outputs a tree that represents the same program in a more structured form. SDF is based mainly on context-free grammars, like EBNF is. It has a number of additions that make it more apt to describe the syntax of really complex programming languages. Especially the languages that were not originally designed to be formally defined, or to have parsers generated for, are the ones that SDF is meant to be applicable to.
These are the unique selling points of SDF, from the language definition point of view:
-
SDF allows modular grammar definitions. This enables the combination and re-use of grammars and makes it easy to handle embedded languages or different dialects of a common base language. It means that you are allowed to write any grammar in SDF, not just LALR(1) or LL(1) grammars.
-
SDF allows more declarative grammars definitions and this results in simpler and more "natural" grammars that are not polluted by idiosyncrasies of particular parsing techniques. This allows an SDF definition to be independent of the implementation of SDF.
-
SDF allows the integrated definition of lexical and context-free syntax.
-
SDF allows declarative disambiguation. For typical ambiguous constructs in programming languages SDF allows you to define a disambiguation with mathematical precision. Note however that SDF does not have a disambiguation construct for every possible ambiguity.
The implementation of SDF is the combination of an SLR(1) parse table generator and a scannerless generalized LR parser.The goal of this implementation is to fully implement all expressiveness that is available in SDF, and avoiding any hidden implementation details.
These are the unique selling points of the implementation of SDF, from the parser generation point of view:
-
There is no seperate scanner. This prevents all kinds of "lexical ambiguity" to occur at all, simply because the parser has more context information.
-
It accepts all context-free grammars, including the ambiguous ones. Many programming languages do not only have LR(1) conflicts, they truly have ambiguous syntaxes (like C for example).
-
It generates all ambiguous derivations, so no implicit choices are made. This is done without backtracking, and without the possibility for exponential behavior.
-
It constructs parse trees automatically, and the optional mapping from parse trees to abstract syntax trees is also provided.
-
It implements the SDF disambiguation constructs as parse tree filters in an efficient manner.
Note that the language definition point of view, and the parser generation point of view are closely related. Because of SDF's focus on the definition of languages and explicitly declaring disambiguations it is particulary well suited for situations that have "language multiplicity":
-
Having to deal with many language dialects (such as in reverse engineering COBOL programs)
-
Dealing with embedded languages (SQL in COBOL/C)
-
Dealing with language extensions (Java with AspectJ)
-
Dealing with domain specific languages (many small languages, and DSL evolution)
The basic assumption of SDF is that all derivations of an input string will be produced. This guarantees that no implicit disambiguation will take place. To disambiguate, the user has to give explicit (declarative) disambiguation rules. Examples of disambiguation rules are longest-match and priorities. By making all these language design choices explicit in a concise manner, SDF allows you to deal with language multiplicity in a more visible (controlled) fashion. In that way high level syntax definition in SDF is like high level programming.
On the one hand, SDF can be used to simply define a language, in order to communicate it as documentation. There are tools that support this use case; checking the definition for inconsistencies and other basic editing support. On the other hand, SDF is often used to obtain a parser for the defined language. Sometimes, SDF is used for other kinds of processing.
Of course you can define an SDF specification in any editor. There is an IDE for SDF called the SDF Meta-Environment, of which the ASF+SDF Meta-Environment is an extension. This IDE supports SDF definition with all kinds of user-interface features (syntax highlighting, static checking, parse forest visualization, metrics and refactoring).
The following references on SDF may be interesting for you:
Warning
TODO Add links!
-
Syntax Analysis, this documents refreshes your knowledge of grammars and parsing in general
-
SDF Disambiguation Med kit for Programming Languages, this document focuses on SDF disambiguation constructs and how to solve common issues when developing SDF grammars
-
Guided Tour: Playing with the Booleans, This interactive demonstrations shows some of the features of SDF in the context of The Meta-Environment
-
SDF definition of SDF, this is the final reference (and implementation) of the syntax of SDF
In this document we describe the syntax of SDF and its basic semantics. It is a basic but complete reference manual for SDF based on small examples. This document is loosely structured according to the syntactic structure of SDF: modules, grammars and symbols. After we have described all of it, we continue with a set of examples. The document ends with special sections on well-formedness, disambiguation and the history of SDF. This document does not detail the usage of the implementations of SDF (sdf2table and sglr).
As an index to this document, the following example exhibits almost all features of SDF with references to the appropriate sections. SDF keywords are highlighted in boldface.
module languages/mylanguage/MyFunnyExample[Param1 Param2] imports basic/Whitespace imports utilities/Parsing[Expr] imports languages/mylanguage/MyExpressions[Expression => Expr] exports sorts Identifier Expr List Stat lexical syntax [A-Z][a-z]+ -> Identifier lexical restrictions Identifier -/- [a-z] context-free syntax Identifier -> Expr {cons("name")} Expr* -> List[[Param1]] "if" Expr "then" {Param2 ";"}+ "else" {Param2 ";"}+ "fi" -> Param2 "if" Expr "then" {Param2 ";"}+ "fi" -> Param2 {prefer} context-free syntax "if" | "then" | "fi" -> Identifier {reject} context-free priorities Expr "&" Expr -> Expr {left} > Expr "|" Expr -> Expr {right} hiddens variables "Id"[0-9\']* -> Identifier lexical variables "Head" -> [A-Z] "Tail" -> [a-z]+
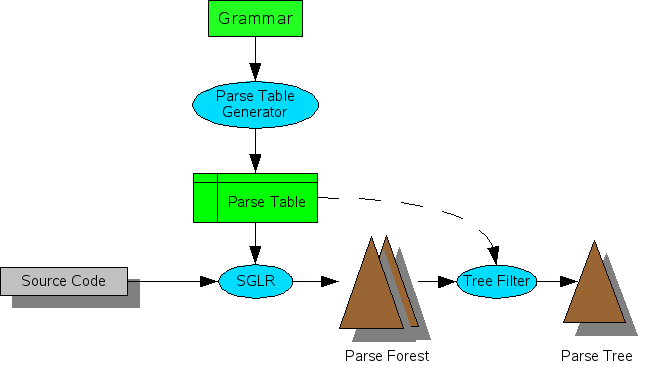
Every SDF grammar has a life-cycle, just like any other software has. This is the life-cycle of an SDF grammar (see also this overview figure):
-
A user types in the modules of an SDF grammar, including the production rules and disambiguation constructs.
-
The modules are concatenated into one single definition.
-
The syntax definition is given as input to the sdf2table tool:
-
The syntax definition is checked for trivial errors by the sdf-checker.
-
The syntax and the disambiguation constructs in the definition are "normalized" to "kernel SDF", by removing all syntactic sugar (expanding macros) and some other stuff.
-
The syntax is used to generate an SLR(1) parse table, and the disambiguation constructs are used to filter some reductions from the parse table
-
-
The resulting parse table can be used by the sglr tool to parse strings. sglr uses some of the disambiguation constructs to filter at parse time, and just after it
-
sglr reads in a file containing a program and outputs a parse forest (or possibly a single parse tree, or a parse error)
-
Other (back-end) tools take the parse forest and do stuff.
At any point in this process something may be erroneous and the process starts from step 1. Step 2 can be done manually by the user, or taken care of by The Meta-Environment. Step 3 and its contributing parts (3.1-3.3) are done by the sdf2table commandline tool, or by the ASF+SDF Meta-Environment. The steps 4 and 5 are done by the sglr commandline tool, or by the ASF+SDF Meta-Environment. Step 6 is open to any other tool that can read ATerms (the output format of sglr).
One more thing, SDF definitions are not only used as input to parser generators. There are tools that generate libraries for syntax tree manipulation, and tools that analyze syntax definitions for example. Recall that the primary goal of SDF is syntax definition, parser generation is the most important secondary goal of SDF.
Although this document is on SDF's syntax and semantics, and not its implementation, the above overview is important. Especially point 3.2 is an essential step for understanding the semantics of SDF. This document describes in several places what certain SDF constructs mean by mapping them to kernel SDF.
An SDF specification consists of a number of module declarations. The sdf2table commandline tool takes a file with all modules concatenated and the word "definition" in front of them as input. The ASF+SDF Meta-Environment accepts the modules in separate files, each with the extension ".sdf". In that case, an SDF module must be in a file named exactly as the name of the module.
Each module may define lexical syntax, context-free syntax and disambiguations. Modules may import other modules for reuse or separation of concerns. A module may extend the definition of a non-terminal in another module. A module may compose the definition of a language by importing the parts of the language.
Note
SDF modules do not hide names in principle, there is no "private/public" mechanism. So beware of name clashes. Later we will see how the renaming facility can be used to solve name clashes declaratively. There is an "hiddens/exports" mechanism however, but it does not only hide names, it also hides the complete definitions from importing modules. More on that mechanism later too.
The basic structure of a module is this. The module keyword is followed by the module name, then a series of imports can be made, followed by the actual definition of the syntax:
module <ModuleName>
<ImportSection>*
<ExportOrHiddenSection>*
A <ModuleName> is either a simple
<ModuleId> or a
<ModuleId> followed by zero or more parameter
symbols, e.g., <Module>[<Symbol>*], the
symbols will be explained later.
The <ModuleId> may be a compound module name
(i.e. <ModuleId> separated by forward slashes), the
ModuleId reflects the directory structure. For
example basic/Booleans means that the module
Booleans is found in the subdirectory
basic.
An <ExportOrHiddenSection> is either an
export section or a hidden
section. The former starts with the keyword
exports and makes all entities in the section visible
to other modules. The latter starts with the keyword
hiddens and makes all entities in the section local
to the module. So, hidden means that when another module imports that
module, none of the hiddens sections will be present in the composition.
The effect for parser generation is that only the hiddens sections of
top module of an SDF specification contribute to the parser
generation.
An <ExportOrHiddenSection> has thus one
of the two forms:
exports
<Grammar>+or
hiddens
<Grammar>+ A <Grammar> can
be a definition of one of the following:
Each of these entities is described and illustrated in Grammars. Most grammars have Symbols as their basic building blocks. Symbols are the SDF term for terminals and non-terminals. Note that it is possible to have hidden imports as well, this means that the full definition of the import definition is copied in the hiddens section of the importing module.
Modules may have formal symbol parameters, which can be bound by actual symbols using imports. The syntax of module parameters is:
module <ModuleName> [ <Symbol>+ ]
When the module is imported, all occurences of the formal parameters will be substituted by the actual parameters.
The comment convention within an SDF specification is that
characters between %% and the end of line is comment as
well as every character between two % characters
including the newline character. An example of the use of comments is
given below. This definition
also defines the comment convention in SDF itself. More details on
defining layout can be found in the section Restrictions.
Example 1.1. SDF comments
module basic/Comments
imports basic/Whitespace
%% In this module we define the
%% comment convention for SDF.
exports
lexical syntax
"%%" ~[\n]* "\n" -> LAYOUT
"%" ~[\%]+ "%" -> LAYOUT
context-free restrictions
LAYOUT? -/- [\%]
Note that every line that has a %% must be
ended with a newline (even the last line in your SDF module
file).
The elementary building block of SDF syntax rules is the symbol. It is comparable to terminals and non-terminals in other grammar definition formalisms. The elementary symbols are: literal, sort and character class.
Since there is no real separation between lexical syntax and context-free syntax in SDF, only character classes are real terminal symbols. Sorts are user-defined non-terminals. All other symbols are short-hands for non-terminals for which the productions are generated for you by SDF (i.e. not user-defined non-terminals). You may view these automatic symbols as macros that generate frequently used grammatical design patterns for you.
Starting with the elementary symbols, more complex symbols can be constructed by way of recursive symbol application. Examples of the use of the various operators will be given in the section Examples.
Remember that complex symbols such as, parameterized sorts, lists and optionals are nothing but non-terminals. They carry no additional semantics from the SDF point of view. However, there are back-ends (tools applied after parsing) which attribute special semantics to these kinds of symbols. ASF+SDF as a rewriting language is an example of a back-end that provides additional semantics to SDF's symbols (but only after parsing).
Symbols are an orthogonal feature of SDF. All symbols of SDF are allowed in both lexical and context-free syntax, priorities and other parts of SDF.
A literal symbol defines a fixed length word.
This usually corresponds to a terminal symbol in ordinary BNF grammars,
e.g., "true" or "&". Literals
must always be quoted, also the literals consisting of letters only. SDF
generates automatically one production for each literal in order to
define it in terms of terminal symbols.
lexical syntax "definition" -> Definition
will generate:
[d][e][f][i][n][i][t][i][o][n] -> "definition"
The above obviously generates a case-sensitive implementation of the defined literal. There are also case-insensitive literals. They are defined using single quotes as in 'true' and 'def-word'. SDF generates a different production to implement case insensitivity:
[dD][eE][fF][\-][wW][oO][rR][dD] -> 'def-word'
In literals, the following characters are special and should be escaped:
-
": double quote (\") -
\: escape character (\\).
Warning
TODO, lookup escaping conventions of literals and ci literals.
A sort corresponds to a non-terminal, e.g.,
Bool. Sort names always start with a capital letter
and may be followed by letters and/or digits. Hyphens
(-) may be embedded in a sort name. Sort names should
be declared in a sorts section to allow some static
consistency checking.
Sort names can have parameters. Parameterized sorts can be used to
implement grammar polymorphism, and to facilitate grammar reuse without
clashing sort names. It provides a way of distinguishing a
List of integers from a List of booleans, e.g.
List[[Int]], versus List[[Bool]].
The sort parameters are usually instantiated via the parameters of a
module or via renaming. A parameterized sort may have several
parameters, like List[[X,Y]]. See parameters for more details.
Parameterized sorts have the following form:
<Sort>[[<Symbol1>, <Symbol2>, ... ]]
Enumerations of characters occur frequently mostly in lexical
definitions. They can be abbreviated by using character
classes enclosed by [ and
]. A character class contains a list of zero or more
characters (which stand for themselves) or character ranges such as, for
instance, [0-9] as an abbreviation for the characters
0, 1, ..., 9.
In a character range of the form
c1-c2
one of the following restrictions should apply:
-
c1 and c2 are both lower-case letters and c2 follows c1 in the alphabet, or
-
c1 and c2 are both upper-case letters and c2 follows c1 in the alphabet, or
-
c1 and c2 are both digits and the numeric value of c2 is greater than that of c1, or
-
c1 and c2 are both escaped non-printable characters and the character code of c2 is greater than that of c1
Escape Conventions Characters
with a special meaning in SDF may cause problems when they are needed as
ordinary characters in the lexical syntax. The backslash character
(\) is used as escape character for the quoting of
special characters. You should use
\c whenever you need
special character c as ordinary character in
a definition. All individual characters in character classes, except
digits and letters, are always escaped with a
backslash.
You may use the following abbreviations in literals and in character classes:
-
\n: newline character -
\r: carriage return -
\t: horizontal tabulation -
\x: a non-printable character with the decimal codex.
Character Class Operators The following operators are available for character classes:
-
~: complement of character class. Accepts all characters not in the original class. -
/: difference of two character classes. Accepts all characters in the first class unless they are in the second class. -
/\: intersection of two character classes. Accepts all characters that are accepted by both character classes. -
\/: union of two character classes. Accepts all characters that are accepted by either character class.
The first operator is a unary operator, whereas the other three are left-associative binary operators. Note that the character class operators are not applicable to symbols in general.
The postfix option operator ? describes an
optional part in a syntax rule. For instance,
ElsePart? defines zero or exactly one occurrence of
ElsePart. SDF generates the following syntax:
-> ElsePart? ElsePart -> ElsePart?
The sequence operator (...) describes the
grouping of two or more symbols, e.g., (Bool
"&"). Sequences are mostly used to group symbols together
to form a more complex symbol using one of the available operators,
e.g., (Bool "&")*. It has no effect to construct
a sequence consisting of a single symbol, because then the (...)
brackets are simply brackets. The empty sequence is a special symbol.
SDF generates the following syntax for the (Bool
"&") symbol:
Bool "&" -> (Bool "&")
For () it simply generates:
-> ()
Repetition operators express that a symbol should occur several
times. In this way it is possible to construct flat lists and therefore
we usually refer to repetitions as \emph{lists}. Repetition operators
come in two flavors, with and without separators. Furthermore, it is
possible to express the minimal number of repetitions of the symbol: at
least zero times (*) or at least one time
(+). Examples are:
-
Bool*(a list of zero or moreBools). -
{Bool ","}+(a list of one or moreBools separated by comma's).
Note that the separator may be an arbitrary symbol, but that some back-ends do not support parse trees that contain them. The sdf-checker of the ASF+SDF Meta-Environment will warn you if you use anything but a literal as a separator.
Again, to implement lists SDF simply generates a few production for you, i.e.:
-> Bool*
Bool+ -> Bool*
Bool -> Bool+
Bool+ Bool+ -> Bool+ {left}
-> {Bool ","}*
{Bool ","}+ -> {Bool ","}+
Bool -> {Bool ","}+
{Bool ","}+ "," {Bool ","}+ -> {Bool ","}+ {left}
Note that there are some more productions generated, but they are not shown here. SDF generates more productions to allow arbitrary compositions of * and + lists, and also adds disambiguation filters to deal with the ambiguity this introduces.
The alternative operator | expresses the choice
between two symbols, e.g., "true" | "false"
represents that either a "true" symbol or a
"false" symbol may occur here. The alternative
operator is right associative and binds stronger than any other operator
on symbols. This is important because Bool "," | Bool ";"
expresses Bool ("," | Bool) ";" instead of
(Bool ",") | (Bool ";"). So, in case of doubt use the
sequence operator in combination with the alternative operator.
For "," | ";" SDF generates:
"," -> "," | ";" ";" -> "," | ";"
It is possible to decorate the symbols with labels. The labels have no semantics in SDF, and will be removed before parse table generation. Other tools that take SDF definitions as input, such as API generators make use of the labels.
So, labels are removed by replacing the labelled symbol with the symbol, as in:
mylist:{elem:Stat sep:";"}+
is replaced by
{Stat ";"}+
The tuple operator describes the grouping of a sequence of symbols
of a fixed length into a tuple. The notation for tuples is <
, , >, i.e., a comma-separated list of elements enclosed in
angle brackets. For example, <Bool, Int, Id>
describes a tuple with three elements consisting of a
Bool, an Int and an
Id (in that order). For instance, <true,
3, x> is a valid example of such a tuple.
Tuple is one of the few symbols that actually introduce a fixed syntax, i.e. the angular brackets. You may consider them as an arbitrary shorthand. To define your own short hand, consider the use of parameterized sorts and module parameters.
For <A,B> SDF generates:
"<" A "," B ">" -> <A,B>
The function operator (...=>...) allows the
definition of function types. Left of => zero or
more symbols may occur, right of => exactly one
symbol may occur. For example, (Bool Int) => Int
represents a function with two argument (of types
Bool and Int, respectively) and a
result type Int. The function symbol may be used to
mimick a higher order type system. The function symbol also introduces
some arbitrary syntax (the ( ) brackets).
SDF generates the following syntax for (A B =>
C):
(A B => C) "(" A B ")" -> C
Read this as "something of type (A B => C) may be applied to A and B to become a C". Note that this is the only symbol that is not defined by generating productions with the defined symbol on the right-hand side. The user must still define the syntax for (A B => C) manually like:
"myfunction" -> (A B => C)
The lifting operator `...` translates the name
of an arbitrary complex symbol to a literal syntax definition of that
name. It makes a symbol a part of the defined syntax. An example:
`X?` defines the syntax ("X" "?").
The lifting operator is typically used in combination with parameterized
modules, and specifically for applications of SDF that implement
concrete syntax. The lifting symbol is a reflexive operator, it
generates different syntax for different operators.
Note that the lifting operator is not implemented by defining it using production symbols. This operator is implemented by replacing it with another symbol. Examples:
`"foo"` is replaced by "\"foo\""
`A ?"` is replaced by ("A" "?")
`{A ","}+` is replaced by ("{" "A" "\",\"" "}" "+")
The LAYOUT symbol is a reserved sort name. SDF
does not generate any productions for it. Instead for all
context-free syntax grammars it will distribute
LAYOUT? between all members of the left-hand sides of
all productions. Note that the "?" in LAYOUT? will
take care of some production generation. The user must define all
alternatives for LAYOUT herself. Example:
[\ \t\n] -> LAYOUT
Note that LAYOUT may only be defined in lexical
syntax grammars. The LAYOUT non-terminal is used by back-ends
(independent of SDF) to find out what is irrelevant about a parse tree
and what is relevant. Still, SDF does not attribute any additional
semantics to it. It is just a non-terminal that is distributed over
context-free productions.
A grammar is the entity that can be defined in an export section or hidden section of a module. It is a catch-all notion that covers more than pure grammar productions and includes
-
Imports: include one module in another one.
-
Aliases: abbreviations for complex symbols.
-
Sorts: the non-terminals of the grammar.
-
Start-symbols: the start symbols of the grammar.
-
Lexical syntax: the lexical productions of the grammar.
-
Context-free syntax: the context-free productions of the grammar.
-
Priorities: the disambiguation rules.
-
Variables: definitions of variables.
An SDF module may contain as many grammars of any kind as you need. We will now describe all these kinds of grammars. Also see the Section Examples.
Apart from the import sections at the beginning of each module,
there may be an arbitrary number of import grammar spread through a
module. Each <ImportSection> starts with the
keyword imports followed by zero or more module
names:
imports
<ModuleName>*When importing modules at the topmost level of a module or when the import section occurs within the scope of an exports keyword, all exported entities of the imported module (and of all modules that are imported indirectly by it) become available in the importing module. In addition, they are also exported by the importing module. However, if the import section occurs within the scope of a hiddens keyword, the exported entities are only visible in the importing module but they are not exported by the importing module.
When an imported module has formal parameters, imports can be used to bind them to actual parameters. The syntax is as follows:
imports mylanguage/myModule[<Symbol>+]
Symbol renaming is in fact very similar to parameterization except that it is not necessary to add formal parameters to a module. The mechanism of symbol renaming allows the overriding of one symbol or a set of symbols by another symbol or symbols, respectively. It allows a flexible and concise way of adapting specifications.
imports mylanguage/myModule[ <Symbol> => <Symbol2> ]
Any number of renamings can be given. Note that renamings and module parameters can be combined. Also note that renamings will not be applied to renamed symbols.
Aliases are similar to productions but not quite. An alias is used to define a short hand for a complex or otherwise cumbersome symbol.
aliases
<Sort1> -> <Sort2>
where the alias Sort2 is given to Sort1. An example is ("{" | "<:") from the C programming language. Instead of having to repeat that everywhere you may write:
aliases
("{" | "<:") -> BracketOpen
Aliases are tricky. There are a number of rules you should adhere to:
-
Aliases may not define each other
-
Aliased symbols may not be redefined by another alias
-
Don't forget that aliases are replaced everywhere, even on the right-hand sides of productions
-
Several known other back-ends of SDF deal badly with aliases (see the next point).
-
Be aware of the non-traceability of aliases, because they are substituted before parse table generation time, you will not find them in your parse trees or abstract syntax trees.
Sorts are declared by listing their name in a sorts section of the form:
sorts
<Symbol>*Only plain Sorts and
parameterized Sorts should declared in the
sorts section. The sdf-checker will generate a
warnings. The checker requires that all sorts that occur in some symbol
in the specification are declared. Note however that the sorts
declaration does not carry any semantics other than simply declaring a
name. The checker uses this to warn the SDF user for possible
typos.
Lexical syntax describes the low-level structure of text while context-free syntax describes the higher-level structure. In SDF, these two aspects of syntax are defined in a very uniform manner. In fact, production rules are used to describe both lexical and concrete syntax.
The only difference between the two is that context-free productions are pre-processed somewhat extensively by SDF before parser generation, while lexical productions are not. And, it is important to note that symbols defined in lexical syntax and symbols defined in context-free syntax are in separate name-spaces. Example:
lexical syntax "a" -> A context-free syntax "b" -> A
Here we are defining two different A's: one lexical and one context-free. The two definitions are automatically linked by SDF by the following transformation:
"a" -> <A-LEX> <A-LEX> -> <A-CF> "b" -> <A-CF>
The lexical syntax usually describes the low level structure of
programs (often referred to as lexical tokens.)
However, in SDF the token concept is not really relevant, since only
character classes are terminals. The lexical syntax grammars in SDF
are simply a convenient notation for the low level syntax of a
language. The LAYOUT symbol should also be defined
in a lexical syntax grammar. A lexical syntax consists of a list of
productions.
Lexical syntax is described as follows:
lexical syntax
<Production>*
The context-free syntax describes the more high-level syntactic structure of sentences in a language. A context-free syntax contains a list of productions. Elements of the left-hand side of a context-free function pre-processed before parser generation by adding the LAYOUT? symbol everywhere. Context-free syntax has the form:
context-free syntax
<Production>*
As an example, consider the way SDF pre-processes the following grammar:
context-free syntax
"{" Stat* "}" -> Block
is pre-processed to:
"{" LAYOUT? Stat* LAYOUT? "}" -> Block
which will be then wrapped as in:
"{" <LAYOUT?-CF> <Stat*-CF> <LAYOUT?-CF> "}" -> <Block-CF>
The resulting definitions may look complex, but in fact there are only non-terminals and production rules. The complexity stems from the names of the non-terminals.
The basic building block of a context-free syntax, lexical syntax or variables grammar is the production. It consists of a left-hand side of zero or more symbols, an arrow symbol -> and a right-hand side that contains a symbol and an optional list of attributes. This is summarized as follows:
<Symbol>* -> <Symbol>
A production is read as the definition of a symbol. The symbol on the right-hand side is defined by the left-hand side of the production.
The symbols in a production can be arbitrarily complex but the implementation may impose some limitations on this. Productions are used to describe lexical as well as context-free syntax, variables and lexical variables. Productions also occur in priority grammars. All productions with the same result sort together define the alternatives for that symbol.
The most striking (but also most trivial) difference between SDF and EBNF is the way the production rules are written in SDF. In EBNF one writes production rules as
P ::= 'b' D S 'e'
whereas in SDF this is written as
"b" D S "e" -> P
So, the left- and right-hand side of the production rules are swapped. Otherwise the meaning of an SDF production is the same as a BNF production. Notice however that there is a difference with the | operator. When we write the following in BNF:
A ::= C | D | E
We would write this in SDF:
C -> A D -> A E -> A
Or, we could use the alternative symbol, but that does generate a different grammar:
C | D | E -> A will generate the following grammar: C | D | E -> A C -> C | D | E D -> C | D | E E -> C | D | E
The definition of a lexical, context-free productions and variables may be followed by attributes that define additional (syntactic or semantic) properties of that function. The attributes are written between curly brackets after the non-terminal in the right hand side. If a production rule has more than one attribute they are separated by commas. Productions with attributes have thus the following form:
<Symbol>* -> <Symbol> { <Attribute1>, <Attribute2>, ...}
The following syntax-related attributes exist:
-
{bracket}is an attribute without SDF semantics, but is important nevertheless in combination with priorities. See brackets attribute. -
{left,right,non-assoc,assoc}are disambiguation constructs used to define the associativity of productions. See associativity. -
{prefer}and {avoid} are disambiguation constructs to define preference of one derivation over others. See preferences. -
{reject}is a disambiguation construct that implements language difference. It is used for keyword reservation. See rejects.
-
Arbitrary ATerms may also be used as attributes. Another frequently occurring non-SDF attribute is {cons("<name>")}. There are tools that use this cons attribute to construct abstract syntax trees or to generated API's in C or Java to manipulate syntax trees.
An important detail of SDF is that if two productions are equal, they will not lead to ambiguity. Instead only one of the productions is used to generate the parse table. In other words, the collection of productions that is used to generate a parse table is a set. The identity of a production is computed from its left-hand side and its right-hand side. If the attributes are different, the set of attributes will be merged. Example:
"if" E "then" S -> S {cons("if")}
"if" E "then" S -> S {prefer}
will be merged to:
"if" E "then" S -> S {cons("if"), prefer}
Prefix functions are a special kind of
productions. They have a prefix syntax and are an abbreviation
mechanism for productions written as expected. For instance the
function f(X,Y) -> Z is a prefix function. SDF
automatically replaces all prefix productions by a normal
productions. Example:
f(X,Y) -> Z {cons("f")}
is replaced by
"f" "(" X "," Y ")" -> Z {cons("f")}
Via the lexical or context-free start symbols section the symbols
are explicitly defined which will serve as start symbols when parsing
terms. If no start symbols are defined it is not possible to recognize
terms. This has the effect that input sentences corresponding to these
symbols can be parsed. So, if we want to recognize booleans terms we
have to define explicitly the sort Boolean as a start
symbol in the module Booleans. Any symbol, also
lists, tuples, etc., can serve as a start-symbol. A definition of
lexical start symbols looks like
lexical start-symbols
<Symbol>*
while context-free start symbols are defined as
context-free start-symbols
<Symbol>*Start symbols are short-hand notation, for which SDF generates productions as in:
lexical start-symbols Identifier generates <Identifier-LEX> -> <START> and context-free start-symbols Program generates <LAYOUT?-CF> <Program-CF> <LAYOUT?-CF> -> <START>
Priorities are one of SDF's most often used disambiguation constructs. A priority 'grammar' defines the relative priorities between productions. There is a lot of short-hand notation for doing this concisely. Priorities are a powerful disambiguation construct. The basic priority looks like this:
context-free priorities
<Production> > <Production>
Context-free priorities work on context-free productions, while
lexical priorities work on lexical productions. The idea behind the
semantics of priorities is that productions with a higher priority "bind
stronger" than productions with a lower priority. However, strictly
speaking the semantics of SDF's priorities are that they give rise to
parse forest filters that remove certain trees. If A >
B, then all trees are removed that have a B
node as a direct child of an A node.
Several priorities in a priority grammar are separated by comma's. Productions may be grouped between curly braces on each side of the > sign. Groups may have relative associativity labels. Examples:
context-free priorities { left: E "*" E -> E {left} E "/" E -> E {right} } > { right: E "+" E -> E {left} E "-" E -> E {left} , "-" E -> E > E "+" E -> E {left}
Please note the following details on priorities:
-
By default, the priority relation is automatically transitively closed (i.e. if
A > BandB > CthenA > C) -
By default, the priority relation applies to all arguments of the first production (i.e. the second production can not be a child of any member of the first production)
-
Priorities filter regardlessly, and assume you apply them only when there is actually an ambiguity. Priorities may be used to filter the last remaining tree from a forest, resulting in a parse error.
There are two recent additions to priorities which make them more flexible. Firstly, priorities can now be targeted at specific members of the first production: "priorities in specific arguments". Example:
context-free priorities E "[" E "]" -> E <0> > E "+" E -> E {left}
Between the angular brackets a comma separated list of argument
indexes indicates to which arguments the disambiguation should be
applied (and implicitly in which not). In fact, in this example applying
the filter to all arguments would result in parse errors for terms such
as "1 [ 2 + 3 ]". The semantics of priorities in
specific arguments is thus to remove all derivations that have the
second production as a child of the first production at the specified
positions.
The second addition is non-transitive priorities. In rare cases the automatic transitive closure may be incorrect. Note however that by not transitively closing the priority relation you may have to write down a high amount of priorities. Example:
context-free priorities
"-" E -> E >.
E "+" E -> E
The ".", or full stop, makes sure that this relation does not contribute to any transitive closure.
Variables are declared in the variables section
of a module. Like all other entities in a module, except equations,
variables may be exported (see section Modules). A variables section consists
of a list of variable names followed by a symbol. In fact, a variable
declaration can define an infinite collection of variables by using a
naming scheme instead of a simple variable name. A
naming scheme is a regular expression like the ones allowed in the lexical syntax except that sorts
are not allowed. A variable may represent any symbol. In the
specification below,
Id, Type3, and
Id-list are examples of variables declared by the naming
schemes in the variables section. Strings that occur
in the left-hand side of variable declarations should
always be quoted.
Example 1.2. Variable declarations using naming schemes
module VarDecls
imports basic/Whitespace
exports
context-free start-symbols Decl
sorts Id Decl Type
lexical syntax
[a-z]+ -> Id
context-free syntax
"decl" {Id ","}+ ":" Type -> Decl
"integer" -> Type
"real" -> Type
hiddens
variables
"Id" -> Id
"Type"[0-9]* -> Type
"Id-list"[\']* -> {Id ","}*
"Id-ne-list" -> {Id ","}+
Lexical variables are similar to variables. The difference is that they range over non-terminals defined in lexical syntax sections, and may range over character classes and symbol operators applied to character classes.
The notion of restrictions enables the formulation of lexical disambiguation strategies that occur in the design of programming languages. Examples are "shift before reduce" and "longest match". A restriction filters applications of productions for certain non-terminals if the following character (lookahead) is in a certain class. The result is that specific symbols may not be followed by a character from a given character class. A lookahead may consist of more than one character class (multiple lookahead). Restrictions come in two flavors:
-
lexical restrictions that apply to lexical non-terminals
-
context-free restrictions that apply to context-free non-terminals.
The general form of a restriction is:
<Symbol>+ -/- <Lookaheads>In
case of lexical restrictions <Symbol> may be
either a literal or sort. In case of context-free restrictions only a
sort or symbol is allowed. The restriction operator
-/- should be read as may not be followed
by. Before the restriction operator -/- a
list of symbols is given for which the restriction holds.
Lookaheads are lists of character classes separated by ".". Note that single character restrictions are implemented faster then multiple character restrictions. Example:
Identifier -/- [i].[f] Identifier -/- [e].[l].[s].[e]
The semantics of a restriction <Symbol> -/-
<Lookahead> are thus to remove all derivations that
produce a certain <Symbol>. The condition for this removal is that
the derivation tree for that symbol is followed immediately by something
that matches the lookahead declaration. Note that to be able to check
this condition, one must look past derivations that produce the empty
language, until the characters to the right of the filtered symbol are
found. Also, for finding multiple lookahead matches, one must ignore
nullable sub-trees that may occur in the middle of the matched
lookahead.
Warning
A note on implementation of restrictions is that follow restrictions with one lookahead character class are filtered at parse-table generation time. This is a fast implementation. Follow restrictions with multiple lookahead are implemented at parse time, which takes some more time. On the whole, the application of follow restrictions can make a generated parser a lot faster. Sometimes it is used to remove conflicts from the parse table, even if the language is not ambiguous at all. This may improve speed.
As mentioned before SDF is based on two notions. The first is context-free grammars, and the second is disambiguation filters. The disambiguation constructs of SDF are:
Each disambiguation construct gives rise to a specific derivation filter. So, the semantics of SDF can be seen as two-staged. First, the grammar generates all possible derivations. Second, the disambiguation constructs remove a number of derivations. This section mainly serves as an index to the disambiguation constructs found in the the section called “Grammars”, and it provides additional information where needed.
An extensive "How To" on disambiguation can be found in the SDF Disambiguation Med kit for Programming Languages. In the current document there is only limited "howto" information on this subject.
Priorities are described in the section called “Lexical and context-free priorities”. Note that there is a link between associativity and priorities: priority declarations can contain relative associativities. The {bracket} attribute also plays a role in priorities. The essence of the priority disambiguation construct is that certain vertical (father/child) relations in derivations are removed.
Warning
A note on the implementation of priorities. Although we have defined priorities here to work on direct father/child relations only, the current implementation of SDF will also filter deriviations that are directly linked via a chain of injection productions.
Associativity declarations occur in two places in SDF. The first is as production attributes. The second is as associativity declarations in priority groups. Like with priorities, the essence of the associativity attribute is that certain vertical (father/child) relations in derivations are removed:
-
The {left} associativity attribute on a production P filters all occurences of P as a direct child of P in the right-most argument. This implies that {left} is only effective on productions that are recursive on the right (as in
A B C -> C). -
The {right} associativity attribute on a production P filters all occurences of P as a direct child of P in the left-most argument. This implies that {right} is only effective on productions that are recursive on the left ( as in
C A B -> C). -
The {non-assoc} associativity attribute on a production P filters all occurrences of P as a direct child of P in any argument. This implement that {non-assoc} is only effective if a production is indeed recursive (as in
A C B -> C). -
The {assoc} attribute means the same as {left}
Note that in general associatity attributes are thus intended to
work on production rules with the following pattern: X ... X
-> X.
In priority groups, the associativity attribute can also be found. It has the same semantics as the associativity attributes, except that the filter refers to two nested productions instead of a recursive nesting of one production. The group associativity attribute works pairwise and commutative on all combinations of productions in the group. If there is only one element in the group the attribute is reflexive, otherwise it is not reflexive.
Note that associativity does not work transitively. Another way of defining associativity is to translate associativity attributes to non-transitive priorities in specific arguments.
It is not used by SDF, but some back-ends use it. For example, the
restore-brackets tool uses the bracket attribute to
find productions to add to a parse tree before pretty printing (when the
tree violates priority constraints). Note that most of these tools
demand the production with a {bracket} attribute to have the shape:
"(" X ")" -> X {bracket} with any kind of bracket
syntax but the X being the same symbol on the
left-hand side and the right-hand side.
The connection with priorities and associativity is that when a non-terminal is disambiguated using either of them, a production rule with the {bracket} attribute is probably also needed.
The reject disambiguation construct also filters derivations. For
a production <Symbol>+ -> Symbol {reject}
the semantics is that the set of all derivations for
<Symbol> are filtered. Namely, all derivations
that derive a string that can also be derived from
<Symbol>+ are removed. Another way of saying
this is that the language (set of strings) defined by
<Symbol> has become smaller, namely the set of
strings defined by <Symbol+> is subtracted from
it.
The reject mechanism effectively defines the difference operator between two context-free languages. As such it can be used to define non context-free languages such as anbncn. This is not it's intended use.
Warning
A note on the implementation of {reject} is that the full
semantics are not implemented by the current implementation of SDF.
The {reject} attribute works well for keyword reservation in the form
of productions like "keyword" -> Identifier
{reject}. I.e. the language on the left-hand side
is regular. Note that the {reject} attribute implementation
is known to filter incompletely when:
-
applied to productions that are empty or right-nullable or recursive.
-
the non-terminal on the right-hand side is nullable by another production.
-
there is nested {reject} productions applied to each other.
The preferences mechanism is another disambiguation filter that provides a filter semantics to a production attribute. The attributes {prefer} and {avoid} are the only disambiguation constructs that compare alternative derivations. They are sometimes referred to as horizontal disambiguation filters.
The following definition assumes that derivations are represented using parse forests with "packaged ambiguity nodes". This means that whenever in a derivation there is a choice for several sub-derivations, at that point a special choice node (ambiguity constructor) is placed with all alternatives as children. We assume here that the ambiguity constructor is always placed at the location where a choice is needed, and not higher (i.e. a minimal parse forest representation). The preference mechanism compares the top nodes of each alternative:
-
All alternative derivations that have {avoid} at the top node will be removed, but only if other alternatives derivations are there that do not have {avoid} at the top node.
-
If there are derivations that have {prefer} at the top node, all other derivations that do not have {prefer} at the top node will be removed.
Warning
A note on implementation of preferences is that the current implementation of SDF does not always provide a "minimal parse forest representation". Therefore, it is sometimes hard to see where (at which vertical level) the ambiguity constructor will be, and thus which productions will be at the top to compare the preference attributes.
Restrictions, or follow restrictions, are intended for filtering ambiguity that occurs on a lexical level. They are described in restrictions.
We will now give a sequence of small examples that illustrate the various constructs in SDF:
In the Section Some tricky cases, we give examples of definitions that may lead to some confusion.
Below we give an example
of a simple lexical function definition for defining the first three
words that Dutch children learn to read. The three sorts
Aap, Noot and
Mies, each recognize, respectively, the strings
aap, noot and
mies. The sort LeesPlank (a
reading-desk used in primary education) recognizes the single string
aapnootmies.
Example 1.3. Simple lexical productions
module LeesPlank
imports basic/Whitespace
exports
context-free start-symbols LeesPlank
sorts Aap Noot Mies LeesPlank
lexical syntax
"aap" -> Aap
"noot" -> Noot
"mies" -> Mies
Aap Noot Mies -> LeesPlank
Definitions for lower-case letter (LCLetter),
upper-case letters (UCLetter), lower-case and
upper-case letters (Letter) and digits
(Digit) are shown in the first example below}.
Example 1.4. Defining letter (lower-case and upper-case) and digit
module LettersDigits1
imports basic/Whitespace
exports
context-free start-symbols Letter Digit
sorts LCLetter UCLetter Letter Digit
lexical syntax
[a-z] -> LCLetter
[A-Z] -> UCLetter
[a-zA-Z] -> Letter
[0-9] -> Digit
The next example
gives a definition of the sort LetterOrDigit that
recognizes a single letter (upper-case or lower-case) or digit.
Example 1.5. Defining a single letter or digit
module LettersDigits2
imports basic/Whitespace
exports
context-free start-symbols LetterOrDigit
sorts LetterOrDigit
lexical syntax
[a-z] -> LetterOrDigit
[A-Z] -> LetterOrDigit
[0-9] -> LetterOrDigit
The example below
gives the definition of a single letter or digit using the alternative
operator \/. This definition is equivalent to the one
given above.
Example 1.6. Defining a single letter or digit using the alternative operator
module LettersDigits3
exports
context-free start-symbols LetterOrDigit
sorts LetterOrDigit
lexical syntax
[a-z] \/ [A-Z] \/ [0-9] -> LetterOrDigit
Another example is shown below. This definition of characters contains all possible characters, either by means of the ordinary representation or via their decimal representation.
Example 1.7. Example of character classes
module Characters
imports basic/Whitespace
exports
context-free start-symbols L-Char
sorts AlphaNumericalEscChar DecimalEscChar EscChar L-Char
lexical syntax
"\\" ~[] -> AlphaNumericalEscChar
"\\" [01] [0-9] [0-9] -> DecimalEscChar
"\\" "2" [0-4] [0-9] -> DecimalEscChar
"\\" "2" "5" [0-5] -> DecimalEscChar
AlphaNumericalEscChar -> EscChar
DecimalEscChar -> EscChar
~[\0-\31\"\\] \/ [\t\n] -> L-Char
EscChar -> L-Char
Consider the language of coordinates and drawing commands presented below.
Example 1.8. Simple context-free syntax definition
module DrawingCommands
imports basic/Whitespace
exports
context-free start-symbols CMND
sorts NAT COORD CMND
lexical syntax
[0-9]+ -> NAT
context-free syntax
"(" NAT "," NAT ")" -> COORD
"line" "to" COORD -> CMND
"move" "to" COORD -> CMND
An equivalent conventional BNF grammar (and not considering lexical syntax) of the above grammar is as follows:
Example 1.9. BNF definition of simple grammar
<COORD> ::= "(" <NAT> "," <NAT> ")"
<CMND> ::= "line" "to" <COORD> | "move" "to" <COORD>
Lexical tokens are often described by patterns that exhibit a
certain repetition. The list symbols described in List Symbols can be used to express
repetitions. The example below
demonstrates the use of the repetition symbol * for
defining identifiers consisting of a letter followed by zero or more
letters or digits.
Example 1.10. Defining identifiers using the repetition operator
*
module Identifiers-repetition
imports basic/Whitespace
exports
context-free start-symbols Id
sorts Letter DigitLetter Id
lexical syntax
[a-z] -> Letter
[a-z0-9] -> DigitLetter
Letter DigitLetter* -> Id
If zero or exactly one occurrence of a lexical token is desired
the option operator described in Optional symbols can be used. The use
of the option operator is illustrated below. Identifiers are defined
consisting of one letter followed by one, optional, digit. This
definition accepts a and z8, but
rejects ab or z789.
Example 1.11. Defining a letter followed by an optional number using the
option operator ?
module Identifiers-optional
imports basic/Whitespace
exports
context-free start-symbols Id
sorts Letter Digit Id
lexical syntax
[a-z] -> Letter
[0-9] -> Digit
Letter Digit? -> Id
Productions with the same result sort together define the lexical syntax of tokens for that sort. The left-hand sides of these function definitions form the alternatives for this function. Sometimes, it is more convenient to list these alternatives explicitly in a single left-hand side or to list alternative parts inside a left-hand side. This is precisely the role of the alternative operator. The example below shows how this operator can be used. It describes identifiers starting with an upper-case letter followed by one of the following:
-
zero or more lower-case letters,
-
zero or more upper-case letters, or
-
zero or more digits.
According to this definition, Aap,
NOOT, and B49 are acceptable, but
MiES, B49a and
007 are not.
Example 1.12. Example of alternative operator |
module Identifiers-alternative1
imports basic/Whitespace
exports
context-free start-symbols Id
sorts LCLetter UCLetter Digit Id
lexical syntax
[A-Z] -> UCLetter
[a-z] -> LCLetter
[0-9] -> Digit
UCLetter LCLetter* | UCLetter* | Digit* -> Id
Note that the relation between juxtaposition and alternative
operator is best understood by looking at the line defining
Id. A parenthesized version of this same line would
read as follows:
UCLetter (LCLetter* | UCLetter* | Digit*) -> Id
As
an aside, note that moving the * outside the
parentheses as in
UCLetter (LCLetter | UCLetter | Digit)* -> Id
yields
a completely different definition: it describes identifiers starting
with an uppercase letter followed by zero or more lower-case letters,
uppercase letters or digits. According to this definition
MiES, B49a and
Bond007 would, for instance, be acceptable. A
slightly more readable definition that is equivalent to the previous one is shown below. In any case, we recommend
to use parentheses to make the scope of alternatives explicit.
Example 1.13. Example of alternative operator |
module Identifiers-alternative2
imports basic/Whitespace
exports
context-free start-symbols Id
sorts UCLetter LCLetter Digit Id
lexical syntax
[A-Z] -> UCLetter
[a-z] -> LCLetter
[0-9] -> Digit
(UCLetter LCLetter*) |
(UCLetter UCLetter*) |
(UCLetter Digit*) -> Id
Definitions of integers and real numbers are shown below. Note the use of the alternative
operator in the definitions of UnsignedInt and
Number. Also note the use of the option operator in
the definitions of SignedInt and
UnsignedReal.
Example 1.14. Lexical definition of Numbers
module Numbers
imports basic/Whitespace
exports
context-free start-symbols Number
sorts UnsignedInt SignedInt UnsignedReal Number
lexical syntax
[0] | ([1-9][0-9]*) -> UnsignedInt
[\+\-]? UnsignedInt -> SignedInt
UnsignedInt "." UnsignedInt ([eE] SignedInt)? -> UnsignedReal
UnsignedInt [eE] SignedInt -> UnsignedReal
UnsignedInt | UnsignedReal -> Number
The specification below,
gives the lexical definition of strings which may contain escaped double
quote characters. It defines a StringChar as
either
-
zero or more arbitrary characters except double quote or newline, or
-
an escaped double quote, i.e.,
\".
A string consists of zero or more StringChars
surrounded by double quotes.
Example 1.15. Lexical definition of String
module Strings
imports basic/Whitespace
exports
context-free start-symbols String
sorts String StringChar
lexical syntax
~[\"\n] -> StringChar
[\\][\"] -> StringChar
"\"" StringChar* "\"" -> String
Context-free syntax often requires the description of the repetition of a syntactic notion or of list structures (with or without separators) containing a syntactic notion. The list symbols can be used for this purpose. Lists may be used in both the left-hand side and right-hand side of a context-free function as well as in the right-hand side of a variable declaration.
Here is an example of how lists can be used to define the syntax of a list of identifiers (occurring in a declaration in a Pascal-like language).
Example 1.16. Definition of a list of identifiers
module Decls
imports basic/Whitespace
exports
context-free start-symbols Decl
sorts Id Decl Type
lexical syntax
[a-z]+ -> Id
context-free syntax
"decl" {Id ","}+ ":" Type -> Decl
"integer" -> Type
"real" -> Type
A context-free syntax may contain productions that do not add
syntax, but serve the sole purpose of including a smaller syntactic
notion into a larger one. This notion is also known as
injections. Injections are productions
without a name and with one argument sort
like Id -> Data. A typical example is the
inclusion of identifiers in expressions or of natural numbers in reals.
Such a chain function has one of the following
forms:
-
SMALL -> BIG -
{SMALL SEP}* -> BIG -
SMALL* -> BIG -
{SMALL SEP}+ -> BIG -
SMALL+ -> BIG
It is a common misconception that chain rules will not be
represented in the parse tree that sglr outputs. An
injection production is a production like any other, and will lead to a
node in the parse tree. However, some back-ends are known to interpret
chain rules as sub-sort relations. In the example
below the symbols
Nat and Var are injected in
Exp.
Example 1.17. Definition of expressions that uses injections
module Exp
imports basic/Whitespace
exports
context-free start-symbols Exp
sorts Nat Var Exp
lexical syntax
[0-9]+ -> Nat
[XYZ] -> Var
context-free syntax
Nat -> Exp
Var -> Exp
Exp "+" Exp -> Exp
See below for an example of an SDF specification containing labels. Remember that labels do not have semantics in SDF.
Example 1.18. The module basic/Booleans decorated with
labels
module Booleans
imports basic/Whitespace
exports
context-free start-symbols Boolean
sorts Boolean
context-free syntax
lhs:Boolean "|" rhs:Boolean -> Boolean
lhs:Boolean "&" rhs:Boolean -> Boolean
Groups of associative productions define how to accept or reject trees containing related occurrences of different productions with the same priority. They are defined by prefixing a list of context-free productions in a priority declaration with one of the following attributes:
-
left: related occurrences ofFandGassociate from left to right. -
right: related occurrences ofFandGassociate from right to left. -
non-assoc: related occurrences ofFandGare not allowed.
where F and
G are productions appearing in the list.
Below is an example of the
use of grouped associativity.
Example 1.19. More complex associativity and priority definitions
module ComplexExpr
imports basic/Whitespace
imports basic/NatCon
exports
context-free start-symbols E
sorts E
context-free syntax
NatCon -> E
E "+" E -> E {left}
E "-" E -> E {non-assoc}
E "*" E -> E {left}
E "/" E -> E {non-assoc}
E "^" E -> E {right}
"(" E ")" -> E {bracket}
context-free priorities
E "^" E -> E >
{non-assoc: E "*" E -> E
E "/" E -> E} >
{left: E "+" E -> E
E "-" E -> E}
Associativity attributes can be attached to binary productions of
the form S
opS ->
S, where
opS-string
opS-string
opS-string where
S-string is a string produced by symbol
S. The particular associativity associated
with op determines the intended
interpretation of such sentences. We call two occurrences of productions
F and G
related, when the node corresponding to
F has a node corresponding to
G as first or last child. The associativity
attributes define how to accept or reject trees containing related
occurrences of the same function, F:
-
left: related occurrences ofFassociate from left to right. -
right: related occurrences ofFassociate from right to left. -
assoc: related occurrences ofFassociate from left to right. -
non-assoc: related occurrences ofFare not allowed.
Currently, there is no syntactic or semantic difference between
left and assoc, but we may
change the semantics of the assoc attribute in the future. Is
this really true?
Below we give an example of a definition of simple arithmetic expressions with the usual priorities and associativities.
Example 1.20. Simple context-free priority definition
module SimpleExpr
imports basic/Whitespace
imports basic/NatCon
exports
context-free start-symbols E
sorts E
context-free syntax
NatCon -> E
E "+" E -> E {left}
E "*" E -> E {left}
"(" E ")" -> E {bracket}
context-free priorities
E "*" E -> E >
E "+" E -> E
Module parameterization allows the definition of generic modules for lists, pairs, sets, etc. The operations defined in these modules are independent of a specific type. When importing a parameterized module and instantiating the formal by actual parameters the operations become sort specific. Modules can have formal parameters when defining them. The module name is then followed by a list of symbols, representing the formal parameters of this module. The specification below shows an example of a parameterized module. In this example the formal parameters are used in the parameterized sorts as well, in order to increase readability and to avoid name clashes between different instances of the same module.
Example 1.21. Definition of generic pairs
module Pair[X Y]
imports basic/Whitespace
imports basic/Booleans
hiddens
sorts X Y
exports
context-free start-symbols Pair[[X,Y]]
sorts Pair[[X,Y]]
context-free syntax
"[" X "," Y "]" -> Pair[[X,Y]]
make-pair(X, Y) -> Pair[[X,Y]]
first(Pair[[X,Y]]) -> X
second(Pair[[X,Y]]) -> Y
is-pair(Pair[[X,Y]]) -> Boolean
When importing a parameterized module the formal parameters have
to be replaced by actual parameters. The specification below shows an example of a
rather complicated import of a parameterized module. The symbols
Pair[[Boolean,Boolean]] and
Pair[[Integer,Integer]] are the actual parameters of
the module Pair[X Y] in the last import.
Example 1.22. Use of generic pair module
module TestPair imports basic/Booleans imports basic/Integers imports Pair[Boolean Boolean] imports Pair[Integer Integer] imports Pair[Pair[[Boolean,Boolean]] Pair[[Integer,Integer]]]
The specification below shows
an example of the Pair module without parameters. The
idea is to achieve the same effect as parameterization by explicitly
renaming X and Y to the desired
names when Pair is imported.
Example 1.23. Definition of generic pairs
module Pair
imports basic/Whitespace
imports basic/Booleans
hiddens
sorts X Y
exports
context-free start-symbols Pair[[X,Y]]
sorts Pair[[X,Y]]
context-free syntax
"[" X "," Y "]" -> Pair[[X,Y]]
make-pair(X, Y) -> Pair[[X,Y]]
first(Pair[[X,Y]]) -> X
second(Pair[[X,Y]]) -> Y
is-pair(Pair[[X,Y]]) -> Boolean
During import such module symbols can be renamed via symbol
renaming. The specification below shows an example of a
rather complicated import of the module Pair using
renamings. Renaming X to Boolean
is, for instance, written as X => Boolean.
Example 1.24. Use of generic pair module
module TestPair imports basic/Booleans imports basic/Integers imports Pair[X => Boolean Y => Boolean] imports Pair[X => Integer Y => Integer] imports Pair[X => Pair[[Boolean,Boolean]] Y => Pair[[Integer,Integer]]]
In the example below
both let and in may not be
followed by a letter. This example shows how lexical restrictions can be
used to prevent the recognition of erroneous expressions in a small
functional language. The lexical restriction deals with the possible
confusion between the reserved words let and
in and variables (of sort Var). It
forbids the recognition of, for instance, let as part
of letter. Without this restriction
letter would be recognized as the keyword
let followed by the variable ter.
The context-free restriction forbids that a variable is directly
followed by a letter. It does not forbid layout characters between the
letters, e.g. a b is a legal recognizable
string.
Example 1.25. Using restrictions in the definition of a simple functional language
module Functional
imports basic/Whitespace
exports
context-free start-symbols Term
sorts Var Term
lexical syntax
[a-z]+ -> Var
context-free syntax
Var -> Term
Term Term -> Term {left}
"let" Var "=" Term "in" Term -> Term
lexical restrictions
"let" "in" -/- [a-z]
context-free restrictions
Var -/- [a-z]
The next example illustrates the use of restrictions to define a
safe way of layout. Recall that optional layout,
represented by the symbol LAYOUT?, may be recognized
between the members of the left-hand side of a context-free syntax rule.
However, if a such a member recognizes the empty string, this gives rise
to a an ambiguity. This problem is avoided by the definition given below: it simply forbids that
optional layout is followed by layout characters.
Example 1.26. Safe way of defining LAYOUT
module basic/Whitespace
exports
lexical syntax
[\ \t\n] -> LAYOUT
context-free restrictions
LAYOUT? -/- [\ \t\n]
The example shown below illustrates the use of restrictions to extend the previous layout definition with C-style comments. For readability we give here two restrictions whereas the first one is already imported from module basic/Whitespace. The repetition of this first restriction is redundant and could be eliminated.
Example 1.27. Definition of C comments
module Comment
imports basic/Whitespace
exports
sorts ComWord Comment
lexical syntax
~[\ \n\t\/]+ -> ComWord
context-free syntax
"/*" ComWord* "*/" -> Comment
Comment -> LAYOUT
context-free restrictions
LAYOUT? -/- [\ \t\n]
LAYOUT? -/- [\/].[\*]
A frequently asked question is when to use
lexical restrictions and when to use
context-free restrictions. In one of the previous examples the lexical
restrictions on let and in
cannot be defined using context-free restrictions because these keywords
do not "live" at the context-free level. Is it possible to put a lexical
restriction on Var? Yes, but it will have no effect,
because internally the lexical Var is injected in the
context-free Var. The general rule is to define the
restrictions always on the context-free level and not on the lexical
level unless a situation as will be discussed in the next paragraph
occurs. The specification below is an example of an
erroneous use of context-free expressions, because it prevents the
recognition of (abc)def. If we want to enforce the
correct restriction, it is necessary to transform this context-free
restriction into a lexical restriction.
Example 1.28. Erroneous use of restrictions in the definition of simple expressions
module RestrictedExpressions
imports basic/Whitespace
exports
context-free start-symbols Expr
sorts Expr
lexical syntax
[a-z]+ -> Expr
context-free syntax
Expr Expr -> Expr {left}
"(" Expr ")" -> Expr {bracket}
context-free restrictions
Expr -/- [a-z]
In Symbols a number of sophisticated operators, like alternative, option, function, sequence, and tuple are discussed. These operators allow a concise manner of defining grammars. There are, however, a number of issues to be taken into consideration when using this operators.
In the example below,
two different lists are defined, List1 represents a
list of naturals separated by commas whereas List2
represents a list of naturals separated by commas and terminated by a
comma.
Example 1.29. Definition of two list variants
module Lists
imports basic/Whitespace
exports
context-free start-symbols List1 List2
sorts Nat List1 List2
lexical syntax
[0-9]+ -> Nat
context-free syntax
{Nat ","}+ -> List1
(Nat ",")+ -> List2
The choice between two symbols can be defined in two different
ways: by two separate syntax rules or by a single syntax rule using an
alternative operator. Both styles are shown below. The
definition of the binary operators | and
& can be made more concise as shown by
Bool2, however, it is now impossible to express
that & has a higher priority than
|, see Priorities for more details on
priority definitions.
Example 1.30. Two ways of defining | and
&
module Bool
imports basic/Whitespace
exports
context-free start-symbols Bool1 Bool2
sorts Bool1 Bool2
context-free syntax
"true" -> Bool1
"false" -> Bool1
Bool1 "|" Bool1 -> Bool1 {left}
Bool1 "&" Bool1 -> Bool1 {left}
"true" | "false" -> Bool2
Bool2 ("|" | "&") Bool2 -> Bool2 {left}
The combination of lists and optionals or empty producing sorts leads to cycles in the parse tree. Cycles are considered parse errors. The parser will produce an error message whenever during parsing a cycle is detected. No parse tree is constructed in such a case. Cycles will not lead to non-termination during parsing. See below for an example of such a specification.
Example 1.31. Dangerous combination of lists and optionals}
module Cycle
imports basic/Whitespace
exports
context-free start-symbols T
sorts A P T
context-free syntax
"a" -> A
A? -> P
"[" P+ "]" -> TSometimes commenting out parts of a production rule may lead to cycles, because a non-terminal becomes an empty producing non-terminal. This in combination with lists may then produce unexpected cycles.
In order to improve the quality of the written specifications, a number of checks are performed before an SDF specification is transformed into a parse table. The checks are performed on two levels: the first level are SDF specific checks, the second level are ASF+SDF specific checks. There are various categories of messages in The Meta-Environment
-
Parse errors.
-
SDF type check warnings.
-
SDF type check errors.
We will briefly discuss each of the error messages and indicate what is exactly wrong in the specification. Furthermore we will hint at how the error can be fixed.
There are three different types of parse errors:
-
A syntax error, which is reported by pinpointing the exact location in the file and a message like
Parse error near cursoror
Parse error: character '
c' unexpectedor
Parse error: eof unexpected
This means that the parser detected a syntax error in the text to be parsed and cannot proceed its parsing process. Clicking on the error in the
Errorspane moves the cursor to the exact error location and launches if needed the editor. -
A cycle is reported whenever the parser detects a non-terminating chain of reductions; the message is
Cycle: <list_of_production_rules> -
An ambiguity is reported whenever the parser was able to recognize a (part of) the input sentence in different ways and gives the message:
Ambiguity: <list_of_production_rules>
Warning
It would be nice to rewrite this and the next section in the style:
-
Error message
-
Explanation
-
Example of error.
-
Example of correction.
Warnings do not break the specification, but it is advisable to fix them anyway. Often they point out some not well-formed part in the specification.
-
undeclared sorts: This warning indicates that a sort is used which is not explicitly declared, or it is declared but in a hidden section. -
double declared sort: This warning points out that the sort is already declared somewhere in this module, or in one of the imported modules. -
double declared start-symbol: This warning indicates that the start-symbol is previously defined as start-symbol as well. This can be in the current module or in one of the imported modules. -
illegal attribute: {bracket, left, right, assoc, non-assoc}: This warning is generated because the syntactic form of the production rule and the attribute do not match. Given this mismatch the intended behaviour will not be effective. -
used in priorities but undefined: This warning is generated whenever a production rule is used in a priority section which is not defined in this module or in one of the imported modules. It is possible that this production rule will be defined in one of the modules which imports this module. Normally, this indicates a typo. -
inconsistent rhs in priorities: This warning is caused by a production rule which has not the same right-hand side as the other production rules in the priority relation. Whenever this occurs the effect of the expressed priority relation will be ignored. This check is performed modulo injections. -
unknown constructor used in priorities: This warning indicates the use of a constructor which is not used in the corresponding set of production rules with the same right-hand side. This is a very weak check on consistent use of constructor information. -
sort CHAR used in production rule: -
deprecated tuple notation: -
deprecated unquoted symbol notation: -
deprecated non-plain sort definition: -
aliased symbol already declared:
-
module not available: -
start-symbols in <ModuleName> not defined in any right-hand: -
literal in right-hand-side not allowed -
only sort allowed in right-hand-side of lexical-function -
double used label: -
constructor has already been used: The combination of right-hand symbol and the constructor information should be unique. This warning points this out. It is advisable not to ignore this warning. In fact, for the parser these double constructors are no problem, but there are tools based on SDF for which this is problematic.
Any parser generated from an SDF definition should output a representation of all derivations. For example, a parse forest containing all parse trees, or any other representation which encodes/serializes all derivations. A derivation should include all characters of the input and also a trace of all productions that are recursively applied to obtain the derivations. A common representation that is used is parse forest with ambiguity packing nodes serialized as ATerms.
Note that cyclic derivations should also be represented.
The essence of this requirement for SDF derivations is that no information should be thrown away. A derivation represents exactly the grammar that was used to generate it, and the input sentence that was parsed.
The main publications on SDF are (in historical order):
The main publications on implementation techniques related to SDF are:
[BVSV02] Disambiguation filters for scannerless generalized lr parsers. 143--158. Proceedings of the 11th International Conference on Compiler Construction (CC'02). . 2002.
[HK86] A Syntax Definition Formalism. 619--630. ESPRIT'86: Results and Achievements. North-Holland. 1986.
[HKR92] Incremental generation of lexical scanners. 490--520. http://doi.acm.org/10.1145/133233.133240. ACM Trans. Program. Lang. Syst.. 4. 1992.