SDF is based on the formalism of context-free grammars. A context-free grammar formally defines the syntax of a language by production rules. By recursively applying production rules they can be used to generate all strings of a language (hypothetically speaking of course). This nested application of production rules results in a derivation tree (parse tree) for each string of the language. The practical application of context-free grammars comes from using the production rules to parse a string. When we parse a string, we simply try to find the derivation tree that produces exactly the string we are trying to parse. If there is such a tree, the string is in the language; if not we have a parse error.

In many cases there is more than one derivation tree for the same string. This is what we call ambiguity. This may happen for parts of the string too: several sub-derivations for the same sub-string. Since we use the derivation trees later for semantical analysis, it is important to have only one derivation tree. The goal of SDF is to let the language designer explicitly (declaratively) express which derivation is the best.

Frequently, the choice of derivation trees has significant consequences for the semantical interpretation of a string. The most clear example is when we pick the wrong order for the multiplication and addition in an expression language: 1 + ( 2 * 3) is different from (1 + 2) * 3! Other examples are to which nested conditional an 'else branch' belongs (which influences order of statement execution), and syntactic overloading (is 'return(1)' a function call or the builtin return statement?

Real programming languages have ambiguous context-free grammars. They even have ambiguous lexical syntax. Many lexer and parser generator technologies either do not accept any ambiguity, or have builtin "implicit disambiguations", which hide this fact conveniently from the user. When you implement a parser using such a technology, your parser will never complain about ambiguity. However, conceptually there will be disambiguation applied anyway. Similarly, for lexical ambiguity, scanners tend to have a number of built-in rules that shield the user from this complexity. Still the disambiguation concept is there, somewhere under the hood.

SDF does not have any implicit, or hidden, lexical or context-free disambiguation mechanisms.

What do I get from this?

What do I pay for this?

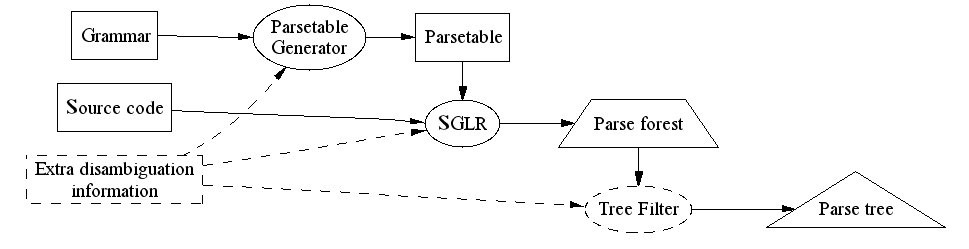
All SDF disambiguation constructs work by the same principle. Each disambiguation construct gives rise to a tree filter. The filter removes exactly the trees that are identified by the disambiguation construct, and no more. This means that when disambiguating in SDF, you are always removing the derivations you do not want, instead of choosing for the derivations you do want. The derivation that you do want is intended to be the only one left in the "forest of derivations", after you have filtered all the others. This also means that you should not write a disambiguation that removes the last tree; that would result in a parse error naturally.

The implementation of filters depends on the information the disambiguation construct uses. Some constructs may be used to filter at parse-table generation time. This prevents the derivation to occur at all. Some filters may be used at parse-time, this prevents further unnecessary computations by the parser. Some filters can be applied only after all derivations are constructed, which is obviously the most expensive alternative. The following figure depicts these ideas:

Figure 1.1. SDF disambiguation architecture

SGLR itself contains some post-parse filters. However, if none of the SDF disambiguation constructs fit your purpose, you may of course write your own filter in your favorite tree manipulation programming language.

This is your Todo list for every ambiguity you wish to resolve:

In case of multiple ambiguities in the same string, try isolating the lower ambiguities in the tree first. Also, if there are cyclic derivations, remove them first to speed up parsing and making the trees look simpler.

Expression languages of programming languages usually have dozens of operators. These operators use infix syntax, prefix syntax, or any other kind of funny syntax. The idea of expressions is that you can recursively combine any of the operators with another. This is why they are sometimes referred to as combinator languages). Like in basic arithmetic, each programming language has a fixed set of rules that explain the relative priority of the expression operators. In programming languages, this can become quite a complex situation. Most programming languages define a partial ordering on the operators, such that all ambiguity is resolved by applying this order. In some programming languages, the order is inconsistent (contradictory), or overly restrictive. SDF allows you to express these properties of languages quite efficiently. You should be able to express all operators using a recursive backbone with a single non-terminal (sort).

As said before, expression operator come in many sizes and shapes. We will consider a number of examples, trying to isolate one particular ambiguous concept in expression grammars at a time.

Associativity of a binary operator

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"       -> E
  E "*" E   -> E
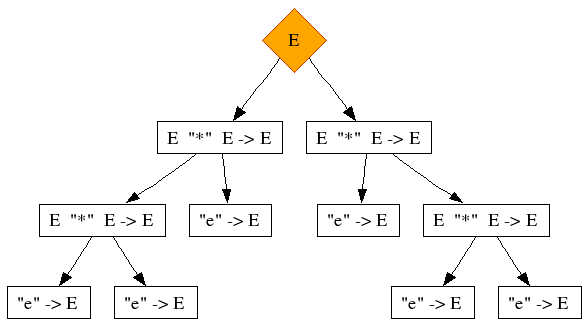
  "(" E ")" -> E {bracket}

This simple grammar is already ambiguous. Let's parse the following string:

e * e * e

This has two possible derivations:

Figure 1.2. A problem with associativity of an operator

We recognize the following symptoms in these trees:

• The top nodes of both alternatives have the same production

• This production has itself as one of its direct children in both derivations

• Which child it is, is different for each derivation. For one it is the left-most child, for the other it is the right-most child

The problem is easily solved by using SDF's associativity attributes:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"       -> E
  E "*" E   -> E {left}
  "(" E ")" -> E {bracket}

The {left} attribute declares that any right-most child of a "*" which is a "*" itself will be filtered. This solves the problem without changing anything else in the grammar. Similarly, you might have used {right} for the opposite solution, or {non-assoc} for filtering all direct children. With {non-assoc} you effectively force the user to write brackets around every recursive application of "*".

Note

The {bracket} attribute is NOT a disambiguation construct. It is used by tree matchers and tree walkers to identify production rules that do not have semantics and may ignored. It is also used by pretty printers to introduce brackets at the appropriate places when necessary.

Priorities between binary operators

The next expression grammar has a different, but related problem:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"     -> E
  E "*" E -> E {left}
  E "+" E -> E {left}

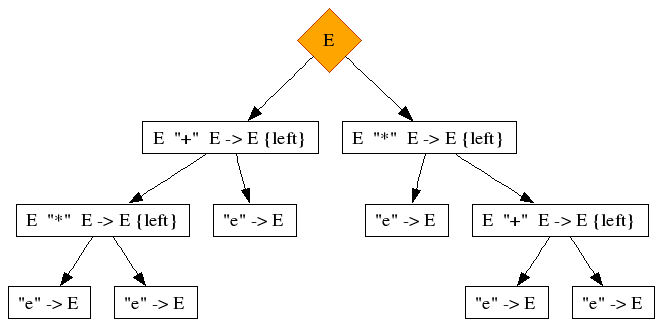
Now we parse this string, and we obtain two trees:

e * e + e

Figure 1.3. A problem with priority between two operators

We observe the following symptoms in these trees:

• The top productions of the two derivations are different

• These two top productions are related to eachother by direct father-child relation. In the one derivation the first is a child of the second, in the other is the first the father of the second.

• Also, in the first derivation the designated father-child relation is on the left child, while in the second derivation it is on the right child.

• The recursion takes place at the extremities: either the left-most or the right-most child of a production is the recursive non-terminal.

Sometimes, these symptoms are called different "vertical ordering issues". They can be solved easily using SDF's priority mechanism:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"     -> E

context-free priorities
  E "*" E -> E {left} >
  E "+" E -> E {left}

The '>' sign declares that all "+" productions that are direct children of "*" productions will be filtered. This leaves the interpretation where the "*" has a higher priority ("binds stronger") as the only derivation.

Note

The production rules that are part of a context-free priorities declaration are automatically promoted to context-free syntax sections. This is to prevent duplication of productions. Sometimes it is still necessary to duplicate a production however. In this case it is good to know that the identity of a production is defined by its left-hand side and right hand side, while if only the attributes are different two productions are considered to be the same.

A different solution to the same issue would be to have both operators have the same priority, but have left or right associativity with respect to eachother:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"     -> E

context-free priorities
{ left:
  E "*" E -> E {left}
  E "+" E -> E {left}
}

Again, "left:" could also be replaced by "right:" and "non-assoc:". It is even possible to have {right} associative productions that are "left:" associative with eachother.

It is important to know that priorities are closed transitively by default. Consider the following example:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e" -> E  

context-free priorities
  "-" E   -> E >
  E "*" E -> E {left}

context-free priorities
  E "*" E -> E {left} >
  E "+" E -> E {left}

- e + e

Figure 1.4. Non-ambiguous application of + to - because of transitive priorities

As you can see, there is no ambiguity, and the "-" has a higher priority than the "+", even though a direct priority was not declared. The ">" relation is closed transitively. A shorter notation for the same module is:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e" -> E  

context-free priorities
  "-" E   -> E        >
  E "*" E -> E {left} >
  E "+" E -> E {left}

Note

In some grammars for programming languages, the priority ordering between expression operators is very complex. It is sometimes not handy to have the priority relation transitively closed. There is a notation in the newest releases of SDF to stop the transitive closure. We will see an example of this later.

Prefix expressions applied to binary expressions

In most programming languages there are prefix expressions like "-e". Consider the following ambiguity.

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"     -> E
  "-" E   -> E
  E "+" E -> E {left}

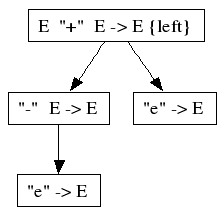
We parse the following string:

- e + e

To get the following two derivations:

Figure 1.5. Prefix production combined with binary production:

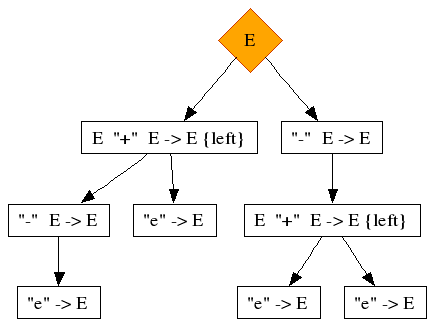
The symptoms are exactly the same as in the two binary operators case, and therefore the solution is also exactly the same. Use priorities to solve the problem!

Postfix expressions with guarded children

So far, we have seen operator productions where the recursive child was either the left-most or the right-most member of a production. Priorities can be applied without reserve to these kinds of ambiguity. In the following case however we need to be more careful.

Consider the following grammar and input string:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"         -> E        
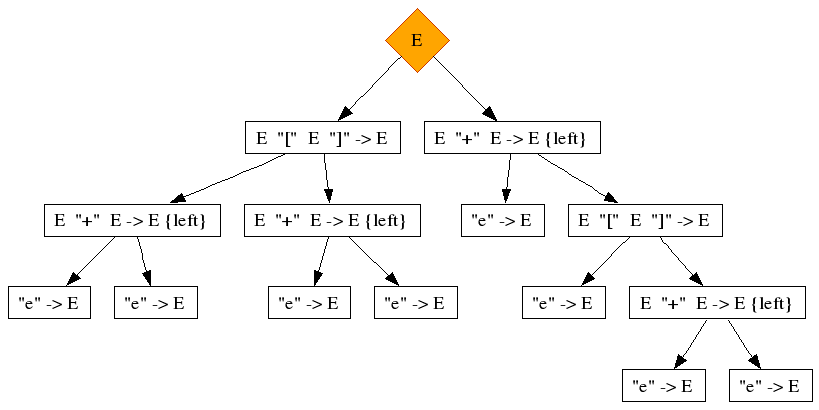
  E "[" E "]" -> E        
  E "+" E     -> E {left}

e + e [ e + e ]

Even though there are three nested applications of operators, there is still only one ambiguity with two alternatives. The reason is that the "[ ]" brackets guard the second "+". It can only be a child of the "[ ]" operator and nothing else. Still the first element of the "[ ]" production is a left-most child, which has a priority issue:

Figure 1.6. Postfix expression with binary operator

Again, these derivations show similar symptoms, but not quite the same:

• The top productions of the two derivations are different

• These two top productions are related to eachother by direct father-child relation. In the one derivation the first is a child of the second, in the other is the first the father of the second.

• Also, in the first derivation the designated father-child relation is on the left child, while in the second derivation it is on the right child.

• The added symptom is that there is no confusion about the second child of the "[ ]". The recursion only takes place at the left-most extremity, the other recursion is not at an extremity.

A plain priority between the two operators would prevent all children of "[ ]" to be "+". This is obviously wrong. The correct solution is to restrict the priority to the first argument of "[ ]":

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"         -> E 

context-free priorities       
  E "[" E "]" -> E <0> >   
  E "+" E     -> E {left}

The "< >" notation is used to restrict the filtering behavior of priorities to certain arguments. In this case, if a "+" is a direct child of the first "E" in the "[ ]" production, it is filtered. No other direct children are filtered but the ones listed between the angular brackets.

It often occurs that there a groups of operators which are similar. Especially with postfix operators this is the case. SDF provides production grouping in priority sections to accomodate this common language design idiom:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e" -> E  

context-free priorities
  { E "[" E "]"        -> E  
    E "(" {E ","}* ")" -> E
  } <0> >
  E "+" E              -> E {left}

In very rare cases, expression grammars get extremely complex and there seems to be no clear order between the operators. In this case, you do not want transitive closure of priorities. These grammars often make frequent use of the priorities for specific arguments. Here is a weird example that uses non-transitive priorities:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"       -> E           
  "(" E ")" -> E {bracket} 

context-free priorities
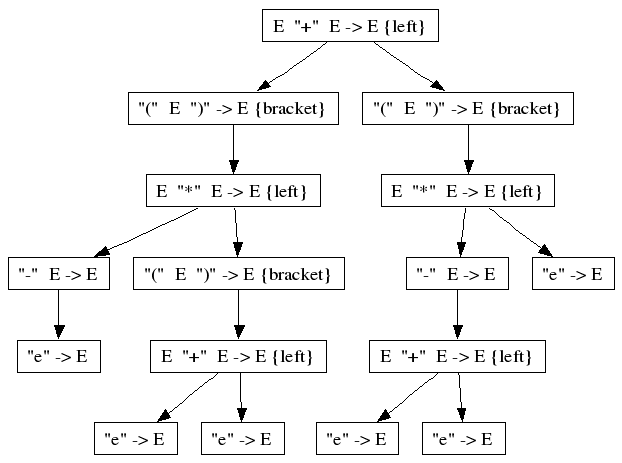
  "-" E   -> E           .>
  E "*" E -> E {left},

  E "+" E -> E {left}  .>
  "-" E   -> E,

{non-assoc:
  E "*" E -> E {left}
  E "+" E -> E {left}
}

In this grammar, the "-" binds stronger than the "*", but weaker than the "+".

(-e * (e + e)) + (-e + e * e)

Figure 1.7. Weird expression grammar with non-transitive priorities between the operators

Note

Grammars with non-transitive priorities are very hard to get correct (where correct means "corresponding to the behavior of some particular compiler or interpreter") . Use a large and thorough test set!

Overloaded comma's in expression languages

In many programming languages arguments of function applications are separated by comma's, and the comma is a binary operator in the expression language. This causes ambiguity as in the following example:

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"                  -> E        
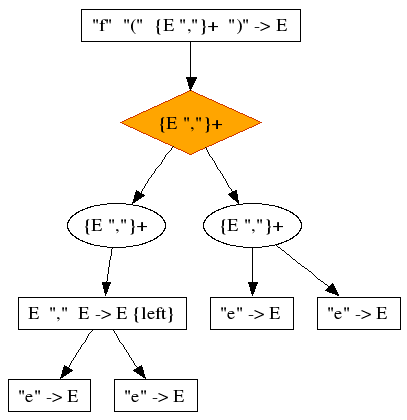
  "f" "(" {E ","}+ ")" -> E        
  E "," E              -> E {left}

f(e,e)

Figure 1.8. Ambiguous comma's in expression languages

The symptoms are easy enough to recognize:

• The ambiguity cluster ranges over a list type

• The top two nodes of each alternative are list nodes

• One of the list nodes has more elements than the other

• The "," literal is shared by the list and another binary production

This kind of ambiguity is solved by removing comma expressions as direct children of argument lists. The priority definition reveals some of the implementation details of SDF, by showing one of the productions that are automatically generated for you. There is no way around this, unless you would like to remove the comma separated argument list and use the binary comma operator instead for parsing your comma's.

module Expressions

exports
sorts E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free start-symbols
  E

context-free syntax
  "e"                  -> E  
  "f" "(" {E ","}+ ")" -> E  

context-free priorities
  { non-assoc: E       -> {E ","}+        
               E "," E -> E        {left}  
  }

Tokenization is a classical technique for parsing programming languages. In some languages it is not done by separating tokens by whitespace, in many languages it is. SDF does not make any assumption about this aspect of language design. There is no implicit "longest match" in SDF. Instead you, as a language designer, will explicitly define the behavior of the parser.

The following is a simple language that requires longest match:

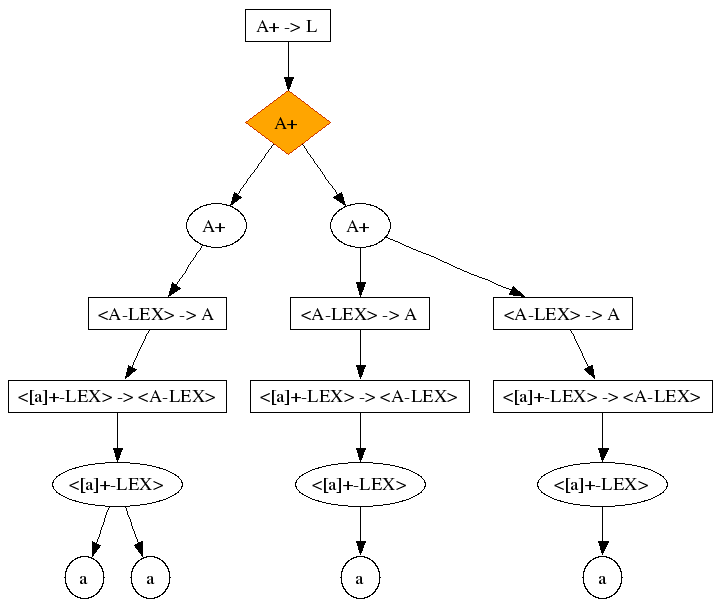
module LongestMatch

exports

sorts A L

context-free start-symbols
  L

lexical syntax
  [\ \t\n] -> LAYOUT
  [a]+     -> A

context-free syntax
  A+ -> L

We parse the following string with it:

aa

Figure 1.9. A tokenization ambiguity

We register the following symptoms:

In other words, the parser has recognized either one long A, or two short A's. A "follow restriction" will solve this problem efficiently:

module LongestMatch

exports

sorts A L

context-free start-symbols
  L

lexical syntax
  [\ \t\n] -> LAYOUT
  [a]+     -> A

context-free syntax
  A+ -> L

lexical restrictions
  A -/- [a]

Naturally, there are more complex situations where longest match is needed. In these cases, you will find that the topnode's of the ambiguity are not necessarily lists. You will find characters that are grouped under one character list node in one alternative, spread out over several other nodes in the other alternative.

As SDF is implemented using scannerless parsing, whitespace and comments are just as important as any other language construct. In SDF you fully define it. There are some common ambiguities related to whitespace and comments that we will discuss here.

Layout nodes moving from left to right

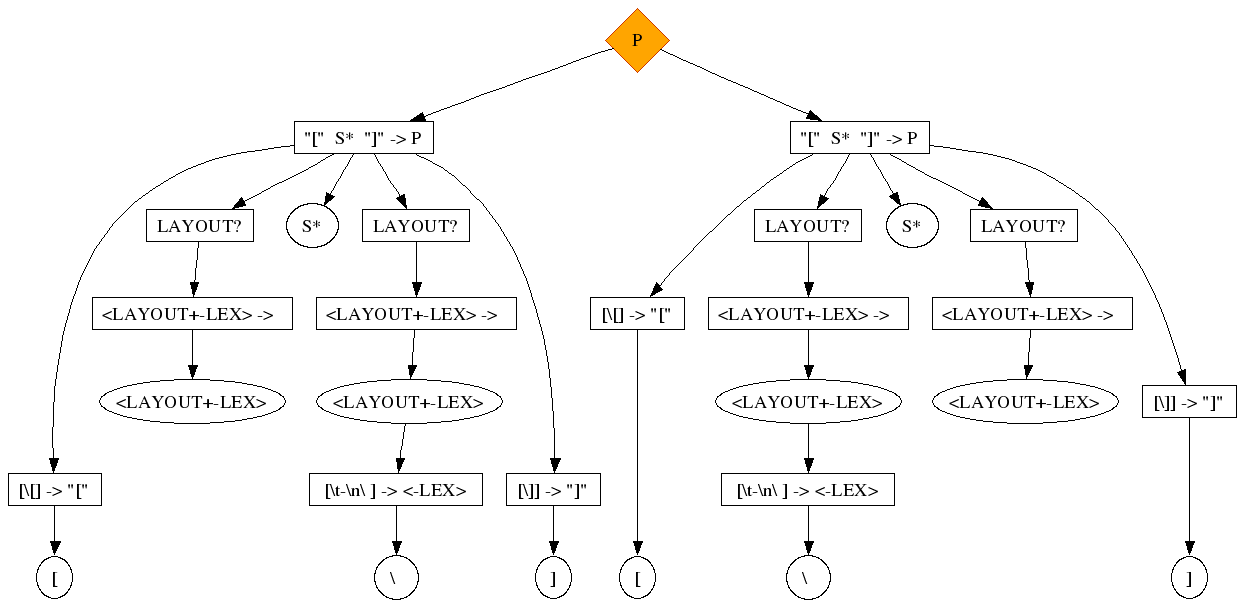
The following simple grammar has a nullable non-terminal in the middle of a production. This triggers already a common ambiguity. Note that star lists like "A*" are nullable non-terminals.

module Layout

exports
sorts P S

context-free start-symbols
  P

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free syntax
  "[" S* "]" -> P  
  "s"        -> S

[ ]

When we parse the above string (two brackets with a space in between), there is a nice ambiguity:

Figure 1.10. Layout moving acros a nullable non-terminal

These trees have typical symptoms:

• There is a nullable symbol (for example a star list) in play,e which indeed recognizes the empty language

• The two layout nodes surrounding the nullable non-terminal take turns in accepting the layout.

SDF introduces the "LAYOUT?" in between every two members in a production that is part of a context-free syntax section. Optional layout is everywhere. The most common solution to this ambiguity is to define that all layout must be recognized with the first "LAYOUT?" node possible:

module Layout

exports
sorts P S

context-free start-symbols
  P

lexical syntax
  [\ \t\n] -> LAYOUT 

context-free restrictions
  LAYOUT? -/- [\ \t\n] 

context-free syntax
  "[" S* "]" -> P  
  "s"        -> S

Notice that the lexical restriction contains every character defined by LAYOUT. Also notice that it is a context-free restriction, not a lexical restriction. The reason is that the LAYOUT? non-terminal is introduced between every non-terminal at the context-free level.

The matter becomes slightly more complex with the introduction of source code comments. In this case, you can define another follow restriction:

module Layout

exports
sorts P S

context-free start-symbols
  P

lexical syntax
  [\ \t\n]       -> LAYOUT 
  "%" ~[\%]* "%" -> LAYOUT

context-free restrictions
  LAYOUT? -/- [\ \t\n]
  LAYOUT? -/- [\%] 

context-free syntax
  "[" S* "]" -> P  
  "s"        -> S

Note

The newly introduced restriction is not always safe. If there are tokens in your grammar that start with a % sign you are in trouble. Be aware of these issues. It could mean that you need more lookahead in the follow restriction.

It is very common to have the keywords of a programming language overlapping with the acceptable characters of identifiers. In some languages, keywords are therefore reserved from the identifier classes. In other languages, they are not reserved at all. SDF can deal with both. Consider the following example:

module Keywords

exports

sorts S E

context-free start-symbols
  S 

lexical syntax
  [A-Za-z][A-Za-z0-9]* -> E
  [\ \t\n]             -> LAYOUT

context-free syntax
  "IF" E "THEN" S "ELSE" S  -> S
  E "=" E ";"               -> S

When we parse the following string, there are no ambiguities at all, even though "IF", "THEN" and "ELSE" fit in the character ranges defined for the sort "E":

IF IF THEN THEN = ELSE; ELSE ELSE = THEN;

Figure 1.11. No reserved keywords necessary

As you can see from the above tree, IF is sometimes recognized as a keyword, and sometimes as an identifier. This depends on the context, which the scannerless parser can figure out automatically.

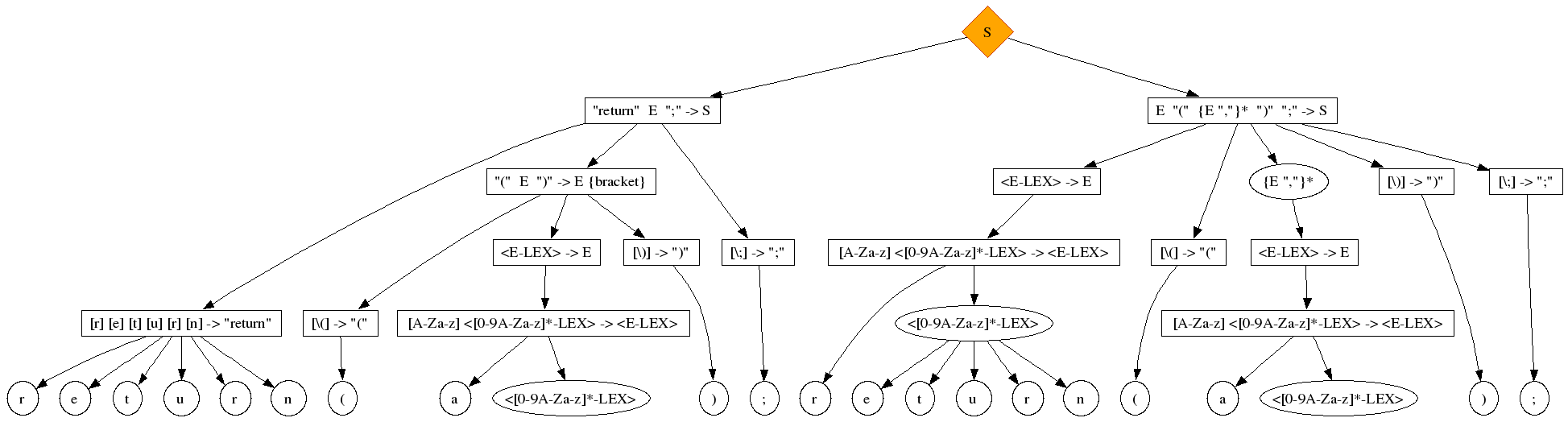
However, in some languages there are not enough syntactical hints for the parser to determine a precise context. In such as case, disambiguation may be required. The following example should look familiar to people who know C, C++, Java or C#:

module Keywords

exports

sorts S E

context-free start-symbols
  S 

lexical syntax
  [A-Za-z][A-Za-z0-9]* -> E
  [\ \t\n]             -> LAYOUT

context-free syntax
  E "(" {E ","}* ")" ";" -> S
  "return" E ";"         -> S
  "(" E ")"              -> E {bracket}

return (a);

When you parse the above string, you will get an ambiguity that must be resolved:

Figure 1.12. Keyword overlaps with identifier

First, let's identify the symptoms of this ambiguity:

There are choices to be made. For many existing languages, the choice is keyword reservation. This implies that no identifier will ever be allowed to be "return". The following grammar implements this:

module Keywords

exports

sorts S E

context-free start-symbols
  S 

lexical syntax
  [A-Za-z][A-Za-z0-9]* -> E
  [\ \t\n]             -> LAYOUT
  "return"             -> E      {reject}

context-free syntax
  E "(" {E ","}* ")" ";" -> S
  "return" E ";"         -> S
  "(" E ")"              -> E {bracket}

The {reject} attribute declares that all identifiers with non-terminal E that match that production will be filtered. This effectively removes the interpretation of the prefix function application, and leafs the other interpretation standing.

However, this also filters all other identifiers that look like "return". For some languages, this is the defined behavior. Other languages are more liberal. Since the top two nodes of the ambiguity differ, we may also apply preference attributes:

module Keywords

exports

sorts S E

context-free start-symbols
  S 

lexical syntax
  [A-Za-z][A-Za-z0-9]* -> E
  [\ \t\n]             -> LAYOUT

context-free syntax
  E "(" {E ","}* ")" ";" -> S
  "return" E ";"         -> S {prefer}
  "(" E ")"              -> E {bracket}

For our example, this has the same disambiguating effect. Added feature is that all other identifiers can still be "return". However, this solution is a bit slower since the preference filter is a back-end filter. And, this solution requires better testing: does this use of prefer deal with all problems introduced by the return keyword?

Programming languages usually have several kinds of identifiers. Consider Java for example, it has class names, variable names, package names, etc. Identifiers, or names, are a common source of ambiguity. Especially when syntax definitions are typed from language manuals, you may expect ambiguities of this kind. Some of the ambiguities are introduced artificially into grammars for ease of implementation with a particular parser technology.

In this class of ambiguities we will identify symptoms that can not be solved by SDF's disambiguation constructs. You will need a name-table for instance. This can be done easily by your favorite tree manipulation library or programming language. ASF+SDF has facilities for manipulating ambiguous parse trees directly.

Useless cloning of identifier classes

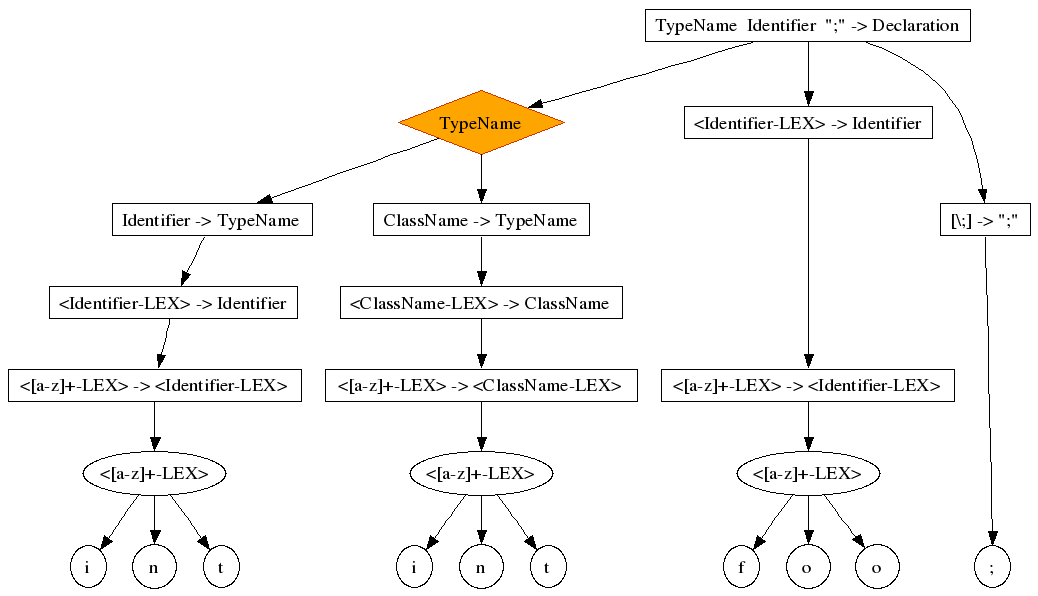
This is a particularly easy ambiguity to solve. You will not even need disambiguation constructs. Consider the following grammar:

module Clone

exports
sorts Identifier ClassName TypeName Declaration

context-free start-symbols
  Declaration

lexical syntax
  [\ \t\n] -> LAYOUT      
  [a-z]+   -> Identifier  
  [a-z]+   -> ClassName   

context-free syntax
  Identifier              -> TypeName     
  ClassName               -> TypeName     
  TypeName Identifier ";" -> Declaration

int foo;

Figure 1.13. A useless clone of an identifier class

The symptoms are very clear:

• The two top productions of the ambiguity are different

• The two top productions of the ambiguity are injections (chain rules)

• Each chain rule introduces a lexical (identifier) that has the same definition, but a different non-terminal name

• Each alternative recognizes exactly the same characters in exactly the same way, modulo non-terminal names

Even if these definitions pop up in language standard documents, they are still useless from the perspective of SDF. They are there to prepare a parser for side-effects that SDF does not have. Ergo, they have to be removed:

module Clone

exports
sorts Identifier Declaration

context-free start-symbols
  Declaration

lexical syntax
  [\ \t\n] -> LAYOUT      
  [a-z]+   -> Identifier  

context-free syntax
  Identifier Identifier ";" -> Declaration

Dynamic identifier reservation

In many languages the basic type names are reserved keywords and they allow the programmer to extend the set of type-names using "class definitions", or "type defs", or anything else that extends the set of types. In these languages, like C for example, the newly identified types become "reserved keywords" immediately after their declaration. This may be the language designers' chosen method to disambiguate the syntax of the language.

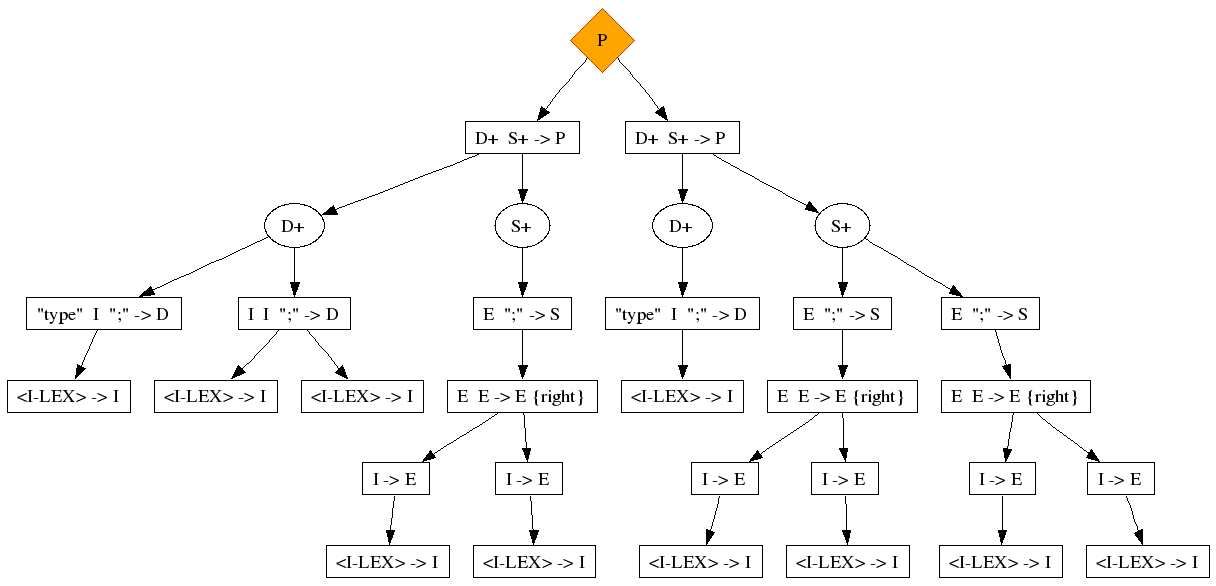
Consider the following example:

module Clone

exports
sorts I D E S P

context-free start-symbols
  P

lexical syntax
  [\ \t\n] -> LAYOUT  
  [a-z]+   -> I       

lexical restrictions
  I -/- [a-z]

context-free syntax
  "type" I -> D
  I I ";"  -> D  

context-free syntax
  I     -> E         
  E E   -> E {right} 
  E ";" -> S         

context-free syntax
  D+ S+ -> P

This example is strongly inspired by the C language definition. The non-terminals names are kept short to make the parse tree viewable in this document (I=Identifier, D=Declaration, E=Expression, S=Statement, P=Program). The following string is ambiguous:

type int;
int i;

Figure 1.14. Dynamically reserved types

The symptoms are complex:

• The top nodes of the two alternatives are equal

• Several syntactic constructs are reused (overloaded) for different purposes. Here, we see the juxtapositioning of two Identifiers both in declarations (D), and in expressions (E), and the ";" is reused. All ingredients are necessary to trigger the ambiguity. If one of them is not there, SDF does not produce this ambiguity.

• Large sub-trees change interpretation, move from one side of the tree to another. In this case, we see a declaration becoming a statement in the other alternative, using completely different productions.

Note

Dynamically reserved identifiers and useless identifier cloning occur together in syntax definitions because the second is used as a method to deal with the first. Not in SDF. Removing the useless clones is a good idea in SDF.

Since dynamic reservation of keywords is far removed from the parsing algorithms SDF defines, this ambiguity can not be solved using any of SDF's disambiguation constructs. You are advised to disambiguate during static analysis. This is a tested method, and can be very successful in generating meaningfull error messages. (Consider the difference between "parse error at line x", and "type or variable X was not declared").

TODO

TODO

TODO

This is a pretty frequently occurring ambiguity, where productions of nested statements or expressions have an optional tail that is not closed by a bracket or other literal. This tail can then sometimes be attributed to an inner or outer production in a derivation tree (when it is the last statement in a nested application). This is one of the more complex ambiguities to identify and to solve. Consider the following (simple) example:

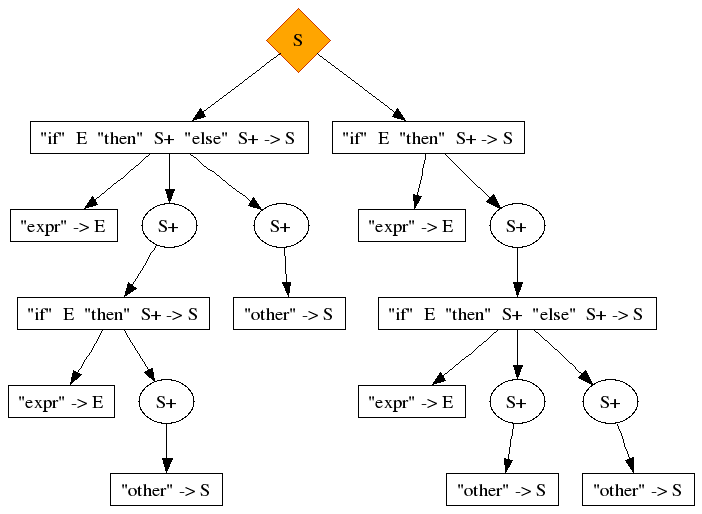
module DanglingElse

exports
sorts S E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free restrictions
  LAYOUT? -/- [\t\n\ ]

context-free start-symbols
  S

context-free syntax
  "expr"                     -> E  
  "if" E "then" S+           -> S  
  "if" E "then" S+ "else" S+ -> S  
  "other"                    -> S

The following string has two derivations:

if expr then 
  if expr then 
    other 
  else 
    other

Figure 1.15. The two derivations for a dangling else

We can recognize the following symptoms in these two trees:

Since the two productions at the top are different here, we may apply the preference attributes. The following definition takes the else branch with the outer if:

module DanglingElse

exports
sorts S E

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free restrictions
  LAYOUT? -/- [\t\n\ ]

context-free start-symbols
  S

context-free syntax
  "expr"                     -> E  
  "if" E "then" S+           -> S {avoid} 
  "if" E "then" S+ "else" S+ -> S  
  "other"                    -> S 

Putting the {avoid} with the other production, will make the parser take the else with the inner if. You may also use the dual of {avoid} which is {prefer}, which works the opposite way.

SDF's priority mechanism are NOT the way to solve this problem. Although we have a vertical order difference here, priorities will not be able to deal with the arbitrary distance between the inner and outer nested statements.

The preference attributes do not work in all cases of dangling else's, or related issues. If the topmost productions are not different, then this construct will not work (we assume here that you have turned off the heuristic filters using "-fe" and "-fi"). Solutions to this are to try and change the grammar such that the top nodes will become different. This is usually done by introducing a "dummy statement terminator", like this:

module DanglingElse

exports
sorts S E 

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free restrictions
  LAYOUT? -/- [\t\n\ ]

context-free start-symbols
  S

context-free syntax
  "expr"                     -> E  
  "if" E "then" S+ T         -> S
  "if" E "then" S+ "else" S+ -> S  
  "other"                    -> S
                             -> T

The dummy statement terminator (T) does not have any syntax, is it a nullable. However, it does make sure that any whitespace after the first S+ is allocated to this statement. This is a technical but important detail that will bring both productions to the same level. Note that it is essential to have the following restriction on LAYOUT? to accomplish this.

A different problem with the preference attributes is that they are implemented in the post-parse phase (which may be too slow for you). A faster, but more complex, solution is to use follow restrictions. The following grammar always attributes the else branch to the inner if. This is by the way what most programming languages with a dangling else do:

module DanglingElse

exports
sorts S E T

lexical syntax
  [\ \t\n] -> LAYOUT  

context-free restrictions
  LAYOUT? -/- [\t\n\ ]

context-free start-symbols
  S

context-free syntax
  "expr"                     -> E  
  "if" E "then" S+ T         -> S 
  "if" E "then" S+ "else" S+ -> S  
  "other"                    -> S  
                             -> T

context-free restrictions
  T -/- [e].[l].[s].[e]

The restriction declares that every T that has "else" directly after it, will be filtered. If only one lookahead character is needed, this filter is resolved at parsetable generation time. In this example however, with four character lookahead the parser will check the lookahead at every reduction for T. You are advised to start with more specific (longer) lookaheads, such that you do not filter too much. Especially if "else" is a reserved keyword in the language, the above disambiguation is safe. If it is not a reserved keyword, you may run into trouble later. This disambiguation filters anything that starts with "else" right after the recognition of T; you have been warned! A safer restriction way would be:

context-free restrictions
  T -/- [e].[l].[s].[e].[\t\n\ ]

This at least guarantees that you do not filter identifiers that accidentally start with "else".

Note that the follow restrictions can not be used to attribute the dangling else part to the outer if.

Some languages solve the dangling construct by the so-called 'offside rule'. With the offside rule, trees are filtered using the 2-dimensional (row,column) position of the dangling construct. SDF does not have a declarative disambiguation construct for expressing this behavior. You will have to implement a filter yourself. You may use the addPosInfo tool to attribute each node in the tree with position information:

$ sglr -p MyLanguage.tbl -i myInputString.txt -fe -fi | \
       addPosInfo -p myInputString.txt -o myOutputTreeWithPosInfo.pt