Regular open sets

Exercise Let A be a subset of a topological space X. How many different subsets can I make starting from A and repeatedly using the closure and interior operations?

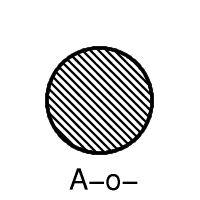
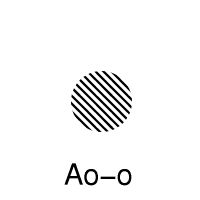
Answer: 7.

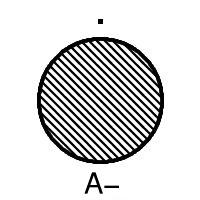
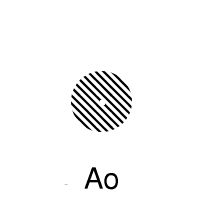
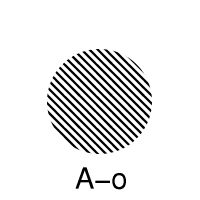
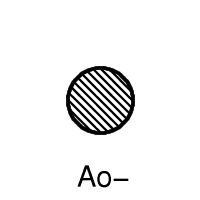
Let us write o for interior and - for closure, so that the closure of the interior of A is written Ao-. Now the seven sets are A, A-, Ao, A-o, Ao-, A-o-, Ao-o. It stops here because A-o-o = A-o and Ao-o- = Ao-.

Proof Since A-o is open, it is contained in A-o-o. Since A- is closed it contains A-o-, and hence A-o contains A-o-o.

Galois Correspondence

Suppose P and Q are partially ordered sets and f:P->Q and g:Q->P order reversing maps. Assume fgf >= f and gfg >= g. Then gfgf = gf. It follows that f and g set up a 1-1 correspondence between gf[P] and fg[Q].

Proof The first inequality yields gfgfp <= gfp for all p, and the second one gfgfp >= gfp for all p.

Of course the same conclusion holds in case fgf <= f and gfg <= g.

Example In a topological space X take for both P and Q the power set of X ordered by inclusion, and take f = g = -c where c is taking complements and - is the closure operator. Indeed, note that c-c = o the interior operator, and A-o- <= A- so that the hypothesis is satisfied. The conclusion says -o-o = -o and o-o- = o-.

Simple Galois Correspondence

Suppose P and Q are partially ordered sets and f:P->Q and g:Q->P order reversing maps. Assume gf >= 1 and fg >= 1, where 1 is the identity mapping. Then fgf = f and gfg = g. If follows that f and g set up a 1-1 correspondence between g[Q] and f[P].

Example Let P be the collection of subfields of a field F and let Q be the collection of subgroups of the group G = Aut F. Define f(K) for a subfield K of F as the group of automorphisms of F that fix K pointwise. Define g(H) for a subgroup H of G as the subfield fixed by H. This is the original Galois correspondence.

Évariste Galois