
Exercise Let A be a subset of a topological space X. How many different subsets can I make starting from A and repeatedly using the boundary and union operations?
Answer: 13.
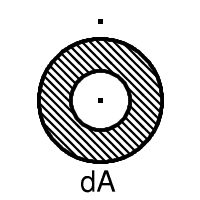
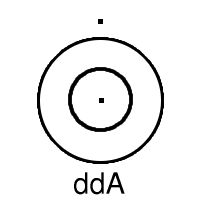
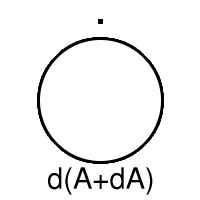
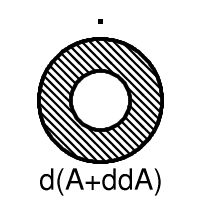
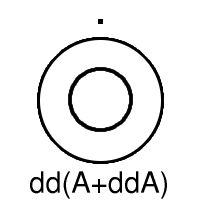
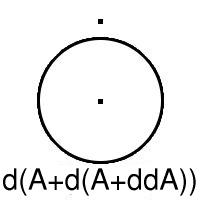
Let us write d for boundary and + for union, so that the closure of A is written A+dA. Now the thirteen sets are A, A+dA, A+ddA, A+d(A+dA), A+d(A+ddA), A+dd(A+ddA), A+d(A+d(A+ddA)), dA, ddA, d(A+dA), d(A+ddA), dd(A+ddA), d(A+d(A+ddA)). (A.E. Brouwer, 1969)
Proof






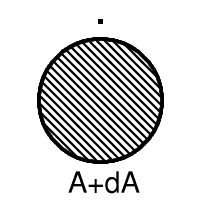

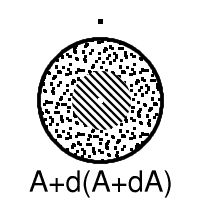

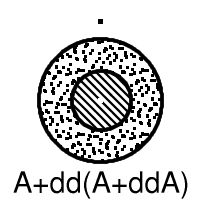
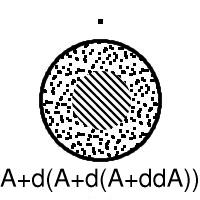
The example shows that one can get thirteen different subsets. It also suggests what we have to prove. Let us shorten notation a bit and write B = A+ddA so that the six boundaries become dA, ddA, d(A+dA), dB, ddB, d(A+dB).
(i) ddC = dC for any closed set C
(in particular for C = dA and C = A+dA).
Indeed, if C is closed then dC is contained
in C, so the interior of dC is contained in
the interior of C which is disjoint from dC,
so dC has empty interior.
(ii) If F is contained in dA,
then d(A+F) contains d(A+dA)
and is contained in dA.
Indeed, d(A+F) is contained in the closure of A
and is disjoint from the interior of A, so lies in dA.
On the other hand, d(A+dA) is contained in d(A+F)
because it is contained in the closure of A+F
(which is the closure of A) and is disjoint from the interior
of A+F (which is contained in the interior of A+dA).
(iii) If C is closed, and D\C = E\C, then dD\C = dE\C.
Indeed, Int(D)\C = Int(D\C).
(iv) ddA + dB = dA and ddB is contained in ddA
and Int(dA) = Int(dB).
Indeed, Since B\ddA = A\ddA we find from (iii) that
dB\ddA = dA\ddA. Applying (iii) once more, we see
ddB\ddA = ddA\ddA. Finally, dB is contained in dA
so Int(dA) is contained in Int(dB), while on the other
hand Int(dA) = dA\ddA = dB\ddA is contained in
dB\ddB = Int(dB).
(v) d(A+d(A+dA)) = dA.
Indeed, by (ii) the LHS is contained in the RHS. By (iii)
it suffices to show that the LHS contains d(A+dA),
and this follows from (ii).
(vi) d(A+ddB) = dA.
Indeed, by (ii) the LHS is contained in the RHS. By (iii)
it suffices to show that the LHS contains ddB.
But the interior of A+ddB is contained in the interior
of A+ddA = B which is disjoint from dB and hence
from ddB.
(vii) ddB + d(A+dB) = ddA.
Indeed, d(A+dB) is contained in ddA since
Int(dA) is contained in Int(A+dB) by (iv).
On the other hand, a point of ddA not in the LHS
lies in dA but not in Int(dA) = Int(dB),
so not in dB but in Int(A+dB), hence in Int(A),
contradiction.
(viii) dd(A+dB) = d(A+dB).
Indeed, a point in the interior of d(A+dB) lies in the
interior of ddA which is empty.
(ix) d(A+d(A+dB)) = dB.
Indeed, using (iii) twice we see that d(A+dB)\dB = dA\dB
and (A+d(A+dB))\dB = (A+dA)\dB and
d(A+d(A+dB))\dB = d(A+dA)\dB which is empty by (ii).
On the other hand, a point of dB that is not in the LHS
lies in the interior of A+d(A+dB), hence in the interior
of A+ddA = B, contradiction.
This settles everything.
