Counting restrictions

For the usual 9x9 Sudokus, the 27 conditions require that each of the 9 rows, the 9 columns, and the 9 boxes contain the digits 1-9.

These 27 conditions are not independent: If 9 row conditions are satisfied, then the entire grid contains each digit 9 times. Now if also 8 column conditions are satisfied, then these columns together contain each digit 8 times, so that the last column automatically contains each digit once, and that last column does not add a restriction.

Similarly, given the row conditions for rows 1,2,3 and the box conditions for boxes 1 and 2, the box condition for box 3 is automatically satisfied. One sees that the boxes add only four independent restrictions.

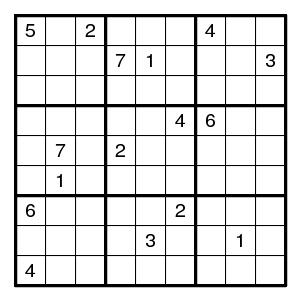
Thus, the usual Sudoku setup has 9+8+4=21 restrictions.

The total number of filled Sudokus is 6670903752021072936960, and in order to arrive at a unique solution some clues (given digits) are needed. The puzzles with the smallest number of clues found so far have 17 clues.

Sudoku with 8 givens

Given additional areas that also must contain a permutation of the digits 1-9 (for example, both diagonals), there are fewer completed puzzles, and fewer clues are needed to guarantee a unique solution.

The usual 27 restrictions are the 9 rows, the 9 columns, and the 9 boxes. Each must contain a permutation of the digits 1-9.

Here I coloured the cells with 9 colours and added the restriction that each colour sees a permutation of 1-9.

(There are 9+8+4+8=29 independent restrictions here.)

Puzzle: complete the below.

Number of restrictions needed?

Second puzzle: investigate the true minimum: how many restrictions are needed such that 8 givens suffice?

For example, here is one with eight colors - one restriction less.

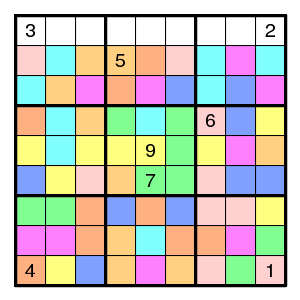
And two with seven colors - again one less.

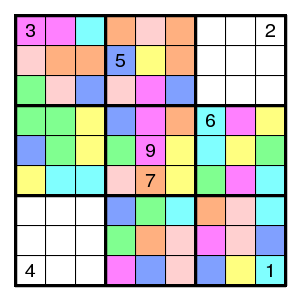
And three with six colors - again one less.

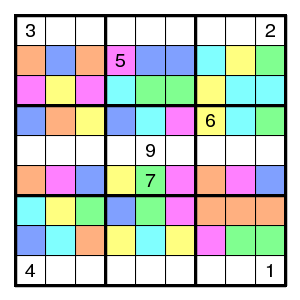
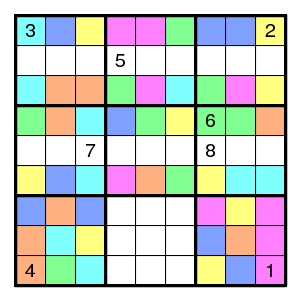
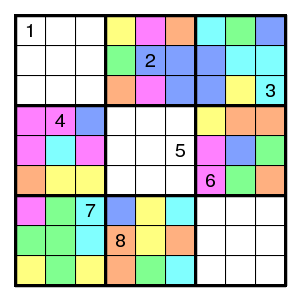
Variation: can one also choose the colour classes in a "nice" way?

The six colors above gave 5 restrictions. Here a version with 5 colors that give 5 restrictions (for a total of 9+8+4+5=26 restrictions).

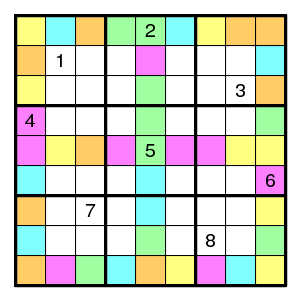
I have not found an example with 4 colors yet.

Du-Sum-Oh - Omitting the standard boxes

One can omit the standard boxes and use a partition into 9 fancy areas instead. The puzzle below, found here, uses 9+8+8=25 independent restrictions.

For more puzzles of this type, see the Du-Sum-Oh page.

Number of givens needed?

If one only gives 7 digits, then two do not occur at all, and in any solution they can be interchanged. Let us say that 7 digits suffice when there are precisely two solutions, so that the partition determined by the digits is uniquely determined. And more generally, that d digits suffice when there are precisely (9-d)! solutions, so that the partition determined by the digits is uniquely determined.

The examples with more than six colors here are best possible in this respect: 0 digits suffice. The examples with six colors (5 restrictions) use their digits. Of course, giving 9 different digits is equivalent to giving a color class, so six colors and 8 digits is almost the same as seven colors and 0 digits.

The Du-Sum-Oh puzzles of order N constructed on this page need 0 digits (with 3N-2 restrictions).

For the ordinary type of Sudoku, several examples are known with 16 givens among which only 7 distinct digits, with 2 completions. E.g. (example by Gordon Royle):