NRC Sudokus
The Dutch newspaper NRC has every Saturday an NRC-Sudoku puzzle.
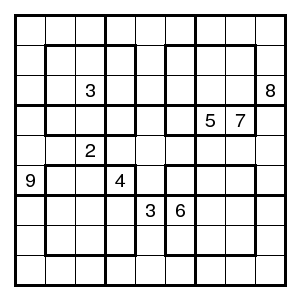
An example from 2005-12-31 (by P. Ritmeester):

One has to complete this grid under the normal Sudoku rules
(each digit 1-9 occurs precisely once in every row, column or box),
but there are 13 boxes instead of the usual 9.
More boxes
For an ordinary Sudoku it is enough to require four boxes
(and the rest will follow automatically, provided
the four boxes do not cover a row or a column,
or form the symmetric difference of a row and a column).
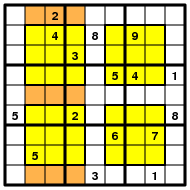
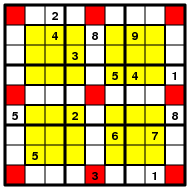
The same holds here: one also has nine boxes - the four given in advance,
and five that follow automatically. In the pictures below the orange box
is a complement of two NRC-boxes in the union of three columns.
There are four of such boxes (two in the union of three columns,
and two in the union of three rows). And the red box is the complement
of the 4+4 found so far. These additional boxes are very useful
when solving NRC-Sudokus - they show that certain cells must have
different digits where this is not immediately apparent.
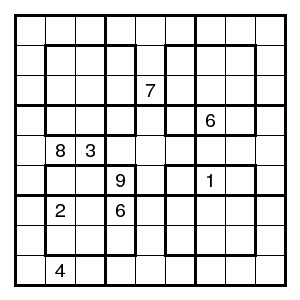
Fewer clues
For ordinary Sudokus the smallest number of clues known
(for a puzzle with unique solution) is 17. Since we have stronger
restrictions here, fewer clues are needed. About 5% of the puzzles
produced by my random NRC-Sudoku generator use 14 clues.
An example:

About 0.1% uses 13 clues. An example:
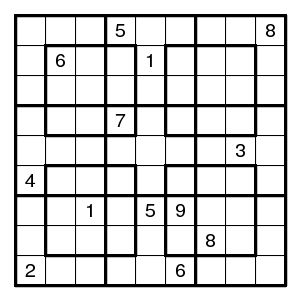
Every now and then one encounters examples with 12 clues.
A dedicated search yields thousands of them.
An example:

A dedicated search yielded a few examples
with 11 clues.
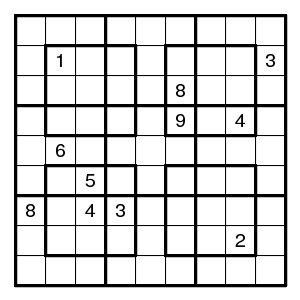
Counting
The total number of completed NRC Sudokus is 6337174388428800.
(Found by aeb, confirmed by Red Ed ("T 145").)
Also requiring the diagonals
A diagonal NRC Sudoku, short NRCX Sudoku, is one where also
both diagonals are permutations. Here two examples with 9 clues.