For each of these 1-1 correspondences between sets X and Y of size 9, if we have identified subsets A and B of X and Y, respectively, of the same size n, for some n between 1 and 9, such that we know that the partners of every element of B must be in A, then A and B are matched, and nothing else has a partner in A.
Let us formulate this more explicitly.
The three matching principles are:
A) If for some set of n positions in a single row, column, or box there are n digits that can be only at these positions, then these positions do contain these digits (and no other digits).and
B) If for some set of n digits there are n positions in a single row, column, or box, that cannot contain any digits other than these, then these digits must be at those positions (and not elsewhere in the same row, column, or box).and
C) Pick a digit d. If for some set of n rows R there is a set of n columns C such that all occurrences of d in these rows must be in one of the columns in C, then the digit d does not occur in a column in C in a row not in R.(and the same with rows and columns interchanged).
Here n is any number between 1 and 9.
For n=1 we called Principle A that of Forced Digits and Principle B that of Forced Positions.
For n=2 we called Principle A that of Double Pairs.
Note that saying that the partners of every element of B must be in A, is the same as saying that the partners of every element of X\A must be in Y\B. In other words, for each application of one of these principles for n there is also one for 9-n with the same conclusion. This means that one may restrict oneself to n at most 4.
Terminology The situations of Principles A and B are called 'hidden n-set' and 'naked n-set', respectively. Principle C is called 'X-wing' for n=2, 'Swordfish' for n=3, 'Jellyfish' for n=4.


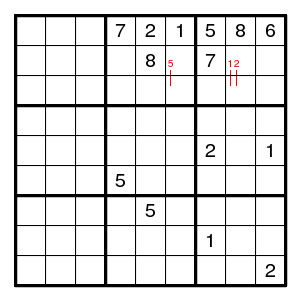
Here the top row is known except for the three digits 3, 4, 9 that must occur in the top left box. These digits must also occur on the second row, and there are only three available places. So these three places contain 3, 4, 9, and the 5 must be on the third row. Another example is given later.
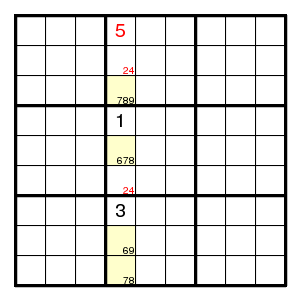
Here the possibilities for the fields in column 4 are given. Note the four yellow fields: together, they only have the four possibilities 6, 7, 8, 9. So, these yellow fields contain 6, 7, 8, 9 in some order, and we can remove 6, 7, 8, 9 from the possibilities of the other fields in that column.
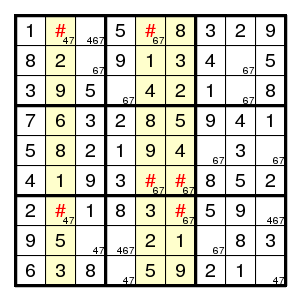
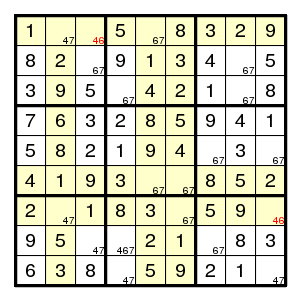
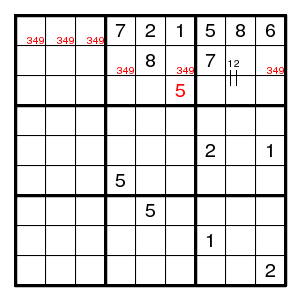
For digit 7, the only possibilities in columns 2, 5, 6 do occur in rows 1, 6, 7. Therefore, digit 7 cannot occur outside columns 2, 5, 6 in these rows.
(More in detail: every digit 7 that occurs in one of the columns 2,5,6 is in row 1 or 6 or 7. Let us call the digits 7 in columns 2,5,6 'yellow sevens'. Since every column contains precisely one digit seven, there are precisely three yellow sevens, and they are in rows 1,6,7. But these rows contain three sevens altogether, so they cannot contain any non-yellow sevens. That eliminates the possibility 7 for cells (row 1, col 3) and (row 7, col 9).)
(Can you complete this puzzle? One approach is to use a forcing chain starting at position (row 1, column 3).)