Prev Up Next

Subsets

Subset Principle Let S be a subset of the set of cells of a partially filled Sudoku diagram, and let for each digit d the number of occurrences of d in S be at most n_d. If the sum of the numbers n_d equals the size of the set S, then the situation is tight: each digit d must occur precisely n_d times in S. In this case we can eliminate a digit d from the candidates of any cell C such that the presence of d in C would force the number of d's in S to be less than n_d.

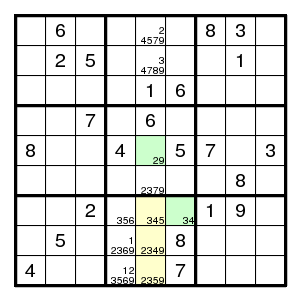
Matching Principle B was the special case where the cells of S are all in one row or column or box. There are many other useful special cases.

Line-box intersection

The argument below was given by Sue de Coq.

Consider the intersection of a line (row or column) and a box. Suppose there are n unsolved cells there, and these have together m candidates, and you can find m-n other cells in the same line or the same box that have no candidates other than these m, and such that for these m-n other cells there is no candidate common to a cell in the same box not on the line and a cell on the same line not in the box. Then matching applies: the m values go into the m cells, and the values can be removed elsewhere.

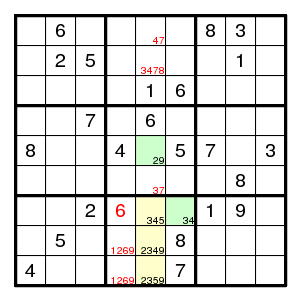
An example given by ronk:

The three yellow squares have together the five possibilities 2,3,4,5,9. The two green squares also have their possibilities inside the set 23459, and since no digit can be seen twice in the yellow and green squares together, these five squares contains these five digits. But that means that 345 can be eliminated elsewhere in the same box, and 259 elsewhere in the same column.

Clearly, this is a special case of the general subset principle.

Extended subset principle

Extended Subset Principle Let S be a subset of the set of cells of a partially filled Sudoku diagram, and let for each digit d the number of occurrences of d in S be at most n_d. If Σn_d = |S| + δ then we can eliminate a digit d from the candidates of any cell C such that the presence of d in C would force the number of d's in S to be less than n_d - δ.

Almost Locked Sets

If A and B are two disjoint sets of cells such that each of them has one more candidate than its size, and there is a digit e that is candidate for both but can occur in at most one, then one may eliminate a digit d different from e that is a common candidate for both A and B from a cell C outside A and B whenever C is adjacent to all possible cells in A or B that have candidate d.

(This is the special case δ = 1 of the extended subset principle: S is the union of A and B, and the condition on e makes sure that Σn_d is at most |A| + |B| + 1.)

Terminology A 'locked subset' is one with as many candidates as its size. An 'almost locked subset' is one with one more candidate than its size.

The above observation is due to bennys. He gave the following example.

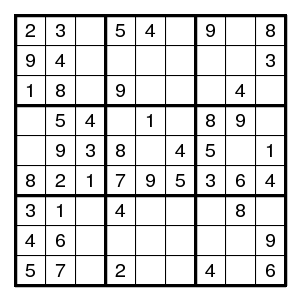
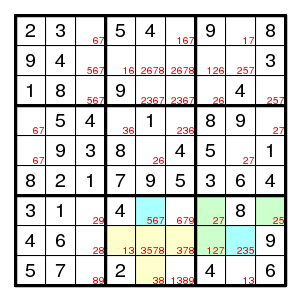
Starting from the given puzzle one arrives after some work at the situation with candidates as shown. Let the sets A and B be the yellow and green sets. A has size 4 and candidates 1,3,5,7,8. B has size 3 and candidates 1,2,5,7. So both are almost locked. The digit 1 is candidate for both but can occur only in one. So, the candidate 5 can be removed from both blue fields.

Thinking in terms of the extended subset principle, it is not necessary to separate the yellow and green sets. Their union is a single set of size 7, and the digits 1,2,3,5,7,8 can occur at most 1,1,1,2,2,1 times, for a total of 8. So δ=1, and every placement that eliminates 2 candidates is wrong. But a 5 at one of the two blue fields would eliminate both 5s and hence cannot occur.

Prev Up Next