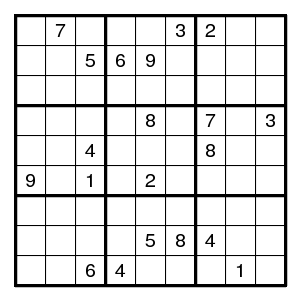
(Preferably, the exploration should happen in one's head. As soon as separate sheets of paper, or an eraser, are involved, it smells more like backtrack.)
Terminology One mostly sees Nishio used in two ways: (i) Choose a value for a single cell, and look at the consequences. If a contradiction is found, then that eliminates the chosen value as a possibility. (ii) Choose a value d for a single cell, and look whether given this value it still is possible to place all other digits d. This second version - which may be the correct version - is much more limited than the first.

By the usual arguments this is completed to
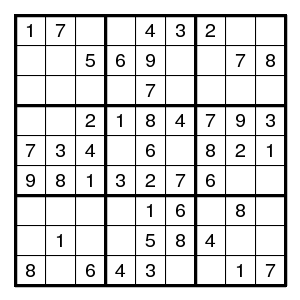
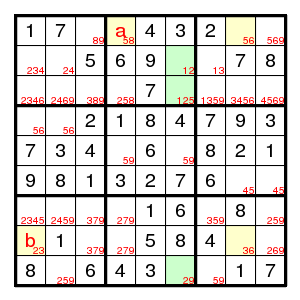
What next? One possible argument uses the forcing chain 85-56-63-32 to see that if field a is 5, then field b is 2. But that is impossible since it forces two 2's in column 6 (and none in column 4): since a is 5, the 2 in the middle top box is in column 6, and since b is 2, the 2 in the bottom row is in column 6. Therefore, a cannot be 5 and must be 8.
This argument can be written as a generalized forcing cycle (1,4)5 > (1,8)6 > (8,8)3 > (8,1)2 > (9,6)2 > (2,6)1 >> (3,6)5 > (1,4)8, where (i,j)d means that digit d is found in row i column j, and > means that the conclusion follows from the previous step in the cycle, and >> means that the conclusion is found from the previous two steps.
Or, much easier, observe that there is a Turbot Fish for the digit 3.
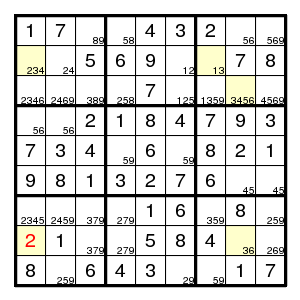
As an example of Nishio (in the narrow sense), observe that there cannot be a 2 at (3,2) or a 3 at (8,1). We just saw that last fact using the Turbot Fish, but the Nishio is even easier (no pencilmarks needed):
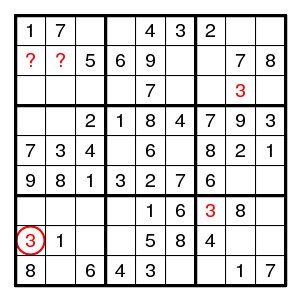
The 3 at (8,1) forces further 3's at (7,7) and (3,8), but then it is impossible to place a 3 in the top left box. So, (8,1) must be 2.
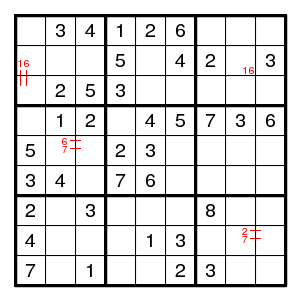
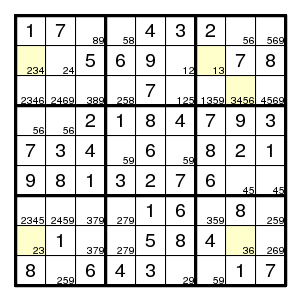
By the usual arguments this puzzle is completed to the given state. Now look where the digits 8 can go. Claim: by Nishio, none of the eight yellow fields can have a digit 8. (And Nishio also shows that there is no digit 9 at (3,6), (9,5).)
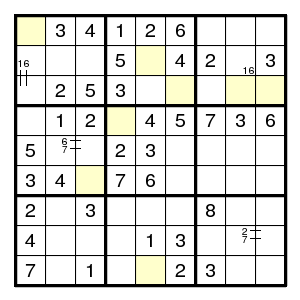
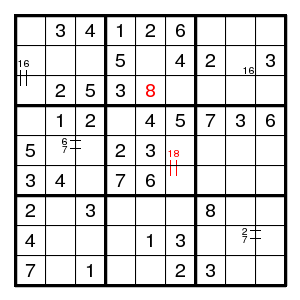
After this observation (and we need only the part that eliminates 8 at (2,5) and (3,6)) the rest is straightforward and requires singles only.
Now what was wrong with 8 at (2,5) or (3,6)? See:
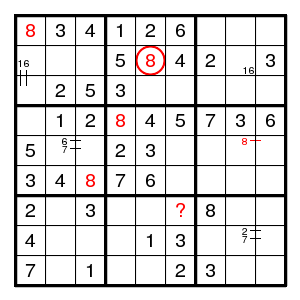
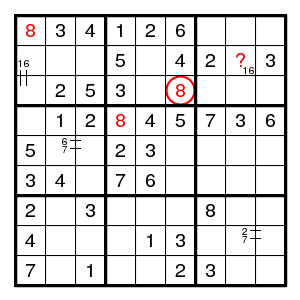
We find (2,5)8 and (1,1)8 and (6,3)8 and (5,[89])8 and (4,4)8 and (?,6)8. There is no room for 8 in column 6, so (2,5)8 is impossible.
Similarly, (3,6)8 and (4,4)8 and (1,1)8 and (2,?)8. There is no room for 8 in row 2, so (3,6)8 is impossible.