A digit from 1 to 9 inclusive goes into each of the eighty-one squares in Figure 1. The same digit does not appear in any row, in any column, or in any 3x3 square. The twenty-three digits shown lead to a unique solution. Find that solution.
*Is it possible to place fewer than twenty-three digits into these eighty-one squares to lead to a unique solution?
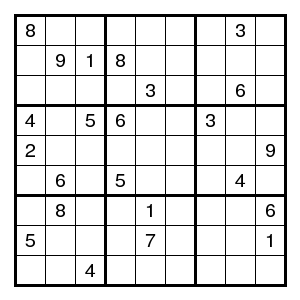
Figure 1.