Signature test

Dave Dyer wrote on his page about signatures

One of the most frustrating tasks in using a collection of game records is locating any particular game; and correspondingly, in maintaining a collection, eliminating duplications when adding in new material. Except for title matches in the final rounds of major titles, there is no "coordinate system" that is commonly used to identify games.

and

This brief paper descibes a simple and effective technique, suitable to find a game when printed diagram of the game is available.

He describes such a coordinate system by assigning as "Signature-A" moves 20,40,60 of the game, and as "Signature-B" moves 31,51,71. Here the move is given as two-letter combination (as in SGF files) with aa for the top left corner, or as ?? when there is no such move.

For similar purposes, but with the entire SGF file available, I found it most useful to work with the MD5 signature of the entire sequence of moves, or the MD5 signature of the sequence of moves truncated to, say, 100 or 50 moves. (Even better, to work with the canonical signature, that is the minimum of the eight MD5 signatures obtained by rotating and reflecting the board. That allows one to identify identical games written down on a rotated board.)

However, both approaches are useful, even when the entire SGF file is present, since a typo in the file will change the MD5 signature, but can leave a Dyer signature unchanged when it does not affect one of the three moves involved.

This page describes an experiment on a collection of 50000 professional games. For a move there are 361 possibilities. For a sequence of N moves, about 19^(2N). If moves were distributed at random over the board, so that all sequences are equally likely, the Birthday Paradox tells us that coincidences become likely when the number of games is larger than the square root of this, that is, is larger than about 19^N. Since 50000 is larger than 19^3 but smaller than 19^4, we should expect to find different games with the same Signature-A or Signature-B, but not many pairs with four coinciding moves in the middle game, and it would be a rare coincidence to find two games where both signatures agree. In fact moves are not that random, and there are more coincidences.

Experiment

Sort games according to Signature-A or -B. The roughly 50000 games had roughly 48650 distinct Sig-A's and roughly 48700 distinct Sig-B's, and roughly 49000 distinct MD5 sums. So, there are only 49000 distinct games in the collection, and in a few hundred cases two different games have the same Sig-A or Sig-B (but not both).

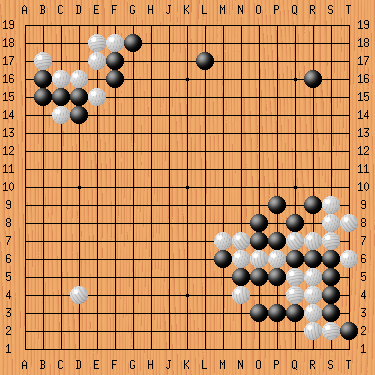
There was an example of four games, all played in 2007, with the same Sig-A (qrsleb) and agreeing on two of the three moves in Sig-B, namely LeeSedol-KimKiyoung37349.sgf, LeeSedol-ChoiCheolhan37348.sgf, YunChanhee-ParkJungsang48995.sgf, AnzaiNobuaki-JinSiyoung46331.sgf, bona fide distinct games with respectively 192, 206, 288 and 349 moves, and Sig-Bs ombdkp, ombdpc, ombdhp, ombdpf. The first and last of these agree on the first 61 moves, the 1st, 2nd and 4th agree on the position after 61 moves (given here),

and the 3rd has a position after 61 moves that differs in only one place (white D3=dq instead of D4=dp). Searching for the pattern obtained by deleting this single move, one finds a fifth game, OnSojin-BaekHongsuk49252.sgf that has the same position rotated counterclockwise over 90 degrees.

(This suggests that the numbers 20, 40, 60, 31, 51, 71 are a bit small, that picking larger move numbers might show greater variation. Unfortunately there are also many games that are resigned comparatively early, where large move numbers only contribute the constant ??.)

Typos

In about 100 cases two games in the collection had different MD5 sums but equal Sig-A and Sig-B. In all cases that meant that the records were actually of the same game, and that one of the two game records had a typo in the sequence of moves.

Tools

The sgfinfo utility (see sgfutils) is able to print MD5 and canonical signatures, and various Dyer-type signatures.

Examples

Two games between Fujisawa Hosai and Go Seigen (1957) resp. Rin Kaiho (1965) start out with the same 73 moves, and hence have the same Dyer signature.

Two games between Park Jungwhan and Park Yeonghun (2014) resp. Huang Yunsong (2016) start out with the same 62 moves and have the same Dyer signature.

Small boards

On a 9x9 board, games tend to take 30-60 moves, and games with less than 31 moves are not unusual. That means that the signature based on moves 20, 40, 60, 31, 51, 71 uses move 20 only, and is not a useful invariant. One can use moves 10, 13, 16, 19, 22 instead.