Mathematical go

There is a book "Mathematical Go" by Berlekamp and Wolfe. Unfortunately, it is unreadable (for me). The authors go on and on, stating facts about special situations, where the reader (me) would like to start with the general idea, the setup, the definitions.

Getting the last point

The idea is very simple. An arbitrary game of go ends in a sequence of moves of smaller and smaller value (apart from the replies to sente moves, which may be forced, that is, of large value), and the final moves have a value of 1 point. If one has arrived at the stage where all moves are worth 1 point, and the difference of the scores of both sides is not more than 1 point, so that the advantage of one side goes 1, 0, 1, 0, ... or ½, −½, ½, −½, ..., the winner (or at least non-loser) is the player who takes the final point, that is, the player who moves last.

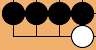
The available number of 1-point moves in a local situation depends in general on the chosen line of play. For example,

allows the sequences B, or W, B, or W, W (with B=black, W=white). (The standard assumption is always that all groups shown are alive, unless the opposite is clear from the diagram. The diagram shows only part of the entire board, and in the remaining part black and white have equally many points.) This means that in

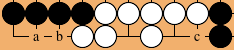
with white to move, white should play at b, then a and c are miai and white wins with 1 point. If white plays at c, then black takes the last point at b and the game ends in jigo. But what if black is to move?

The value of a move

If black starts, we get either B:b, W:c or B:c, W:b, B:a, with jigo in both variations. Strange. How can the final result be the same after either 2 or 3 1-point moves?

What is the value of a move? If we forget about possible ko's, then the value of a move is the difference in outcome (for otherwise perfect play by both players) between playing that move and passing. Aha, but that means that one does not gain by playing that move - if the calculated outcome under perfect play was jigo, and one plays the perfect move one will reach jigo. But if it was a 1-point move and one passes instead of playing that move, one loses by 1 point.

If one wants to use the model where one gains by playing a move, for example in order to play the move that gains most points, then one needs a different model of the value of a move. One needs the model where there is a certain amount of secured territory for both players, and a move adds to one's secured territory, or subtracts from the opponent's secured territory.

Secured territory

Let us say that in a local situation black has N points of secured territory when black gets N points in that local situation under perfect play, no matter who plays first. (And similar for white.) We indicate secure black or white territory by a small black or white dot. (It does not matter where the dots are, only their number matters.) The above diagram becomes

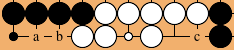
If black plays at b, he gets one more point of secured area:

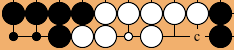
but playing at c does not gain anything from this perspective. That explains why black does not win after starting at c, even though that gets him the final point. The play at c is 1 point better than passing, but does not enlarge the secured area, or diminish the secured area of the opponent.

One more example

Consider the position

with W to move. After W:c the points a and d are miai, and white wins by 1 point. After W:a, B:c the points b and d are miai, and it is jigo. Also after W:d, B:c, W:b, B:a it is jigo. So c is the vital point, both players want to play there.

Next consider the somewhat similar position

with W to move. After W:d, B:c, W:b white wins by 1 point. After W:c, B:d it is jigo. So d is the vital point here.

This shows that one cannot assign values to local positions in such a way that the best move picks the largest value. Here, which of c and d is better depends on the rest of the board.