ARM 9@400MHz; 421 BogoMIPS; 32 MB RAM; 7M for
firmware; 16GB disk; WiFi; web server; Linux; €30.
The last time I had a machine with close to 32M RAM was 1996, with 40M; it cost €4,500. The last time I had a computer with 16G disk was 2000 (with 6G) or 2002 (with 30G); they both cost €2500. (Those computers all had screens and keyboards as well, btw).
You have surely heard of Moore's Law.
It's not actually a law, more a prediction.
In 1965 Gordon Moore predicted that the density of components in integrated circuits would double each year at constant price 'for at least 10 years'.
In 1975 he adjusted that to a doubling every 18 months.
When you turn a tap on, you are adding a certain amount of water per minute to the bath.
So if we look at the graph of the bath filling, we get something like this:
We call this a linear function.
However, for instance, when a bank gives you interest on a bank account, it is not adding a fixed amount every year, but an amount based on how much you have in the bank.
For instance, if they offer a 3% interest, then every year your money gets multiplied by 1.03.
If you have €1000 in your account, then at the end of the year you will have €1000 × 1.03, which is €1030. At the end of the second, you will have €1030 × 1.03, which is €1060.90.
Moore's Law is also a multiplication: a doubling every 18 months (which is 59% annual interest, if you are interested, or about 4% per month).
If we draw a graph of Moore's Law since 1988, it looks something like this:
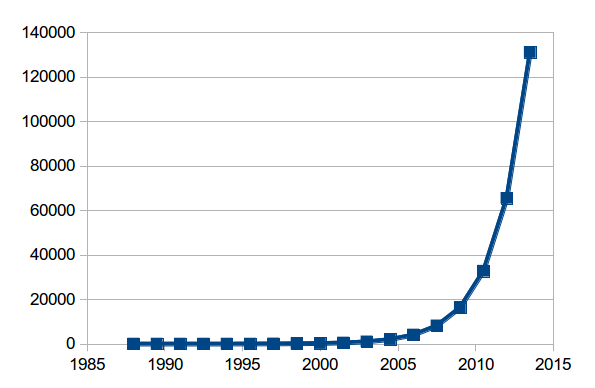
In other words, a computer now is around 130 000 times more powerful than in 1988.
We call this an exponential function.
It is better to graph exponential functions in a different way.
On the vertical axis, rather than going in steps of 1, 2, 3, ... we use steps of 1, 10, 100, 1000, ... Then the exponential graph looks like this:
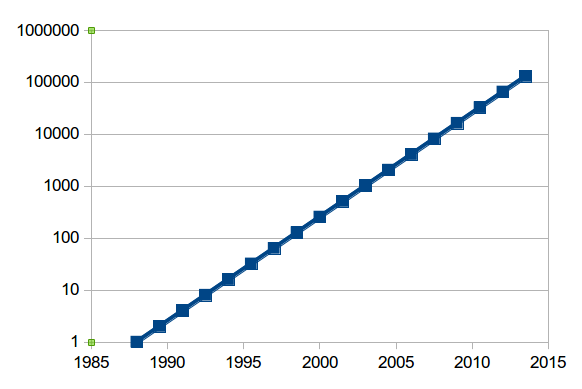
If you use a logarithmic scale, and the graph looks like a line, then it is exponential.
Of course, computers don't get exactly twice as powerful in exactly 18 months.
But I have been collecting data on the power of my computers since 1988.
Ray Kurzweil discovered that Moore's
Law is just one part of a progression going back at least as far as 1900
He calculated how many calculations you get for $1000 using 4 generations of technologies, Electromechanical, Relays, Valves and Transistors, and shows that the progression that we call Moore's Law has been going since at least 1900. Here is computing in 1920.
I have heard very many times that Moore's
Law is nearly over, or (recently) that it is actually over, but that is not so.
Intel recently showed their new 14nm Broadwell chips off, and they still have
at least three shrinkages planned on their timeline.
But even when it does finally come to an
end (for integrated circuits) Kurzweil's finding gives us an expectation that
another technology will replace it.
Often people don't understand the true effects of exponential growth.
A BBC reporter recently: "Your current PC is more powerful than the computer they had on board the first flight to the moon". Right, but oh so wrong.
Take a piece of paper, divide it in two, and write this year's date in one half:
Now divide the other half in two vertically, and write the date 18 months ago in one half:
Now divide the remaining space in half, and write the date 18 months earlier (or in other words 3 years ago) in one half:
Repeat until your pen is thicker than the space you have to divide in two:
This demonstrates that your current computer is more powerful than all other computers you have had put together (and way more powerful than the computer they had on board the first moonshot).
Moore's Law says you get twice as many components in the same area for the same price every 18 months. Size, price, components.
This means you have a choice:
In general we have been optimising this choice: computers have been getting smaller, cheaper and more powerful all at the same time: when you buy a new computer, it is typically a little smaller, a little better, and a little cheaper than the last one you had.
Apparently new home computers peaked in 1990 at $4500. We now pay typically around one tenth of that, for a much more powerful computer.
Each step up in a power of ten is called an order of magnitude change.
Half way between 10 and 100 on a logarithmic scale is about 30 (31.6 to be more exact).
So we say that for an order of magnitude, 30 ≅ 10
Thanks to the effects of Moore's law, each decade or less, there has been an order of magnitude increase in computing power.
This has enabled a new generation of computer to appear.
"An order of magnitude quantitative change is a qualitative change"
As a result we have used each generation of computer in a new way, not just for more of the same.
From the 1950's the way computing was done was on mainframes. These were
room-sized machines, shut off to the outside world, and would cost millions.
They were so expensive that many companies would lease computers rather than buy them.
They often came with 'free' programmers into the bargain.
To rent time on a computer then would cost you of the order of $1000 per hour: several times the annual salary of a programmer!
Starting in the 60's
but picking up momentum in the 70's. Theser were cupboard-sized machines,
costing of the order of ¤100,000.
The disadvantage of these machines were that they were slower, and had few resources (memory, disk) than the mainframes.
But the advantage was that they were cheap, and you could have them in the lab. You still had to share, but it was nearby, and you got instant turnround once you were on it.
Starting in the 70's but picking up momentum in the 80's came the
Workstation, which could go on the desktop of the programmer in the office, and
were known as 3M machines:
Now at last programmers had machines of their own.
![Apple ][](../../2010/01-08-steven-ten-euro-computer/800px-Apple_II.jpg)
Starting
in the late 70's, came the PC, the first computer to make its way into the home
(and the briefcase). It cost of the order of ¤1000.
A PC and a laptop were of roughly the same power, but a laptop was smaller, and therefore more expensive.
Since we have seen
¤1000000 mainframes: locked away
¤100000 minis: in the lab
¤10000 workstations: on the desk
¤1000 PCs: in the home
We really should have expected the emergence of the ¤100 machine, in the form of first Netbooks and then Tablets
One per person instead of one per household.
Carry around.
Light, low powered (but Moore's Law ensures that they are constantly getting more powerful).
Use the cloud for data, rather than large amounts of onboard storage.
So how about the next generation?
It has appeared in the form of the Raspberry Pi.
Price €25. About as powerful as a ¤100 computer from 6 years earlier, or a ¤1000 computer from 10 years earlier.
32kb memory, 16MHz.
With computers available costing around €1, it will be possible to embed computers in everything, kettles, alarm clocks, door bells, light bulbs.
This will drive what is being called The internet of things.
OK, so we all know Moore's Law now.
But often people don't understand its true effects.
Take a piece of paper, divide it in two, and write this year's date in one half:
Now divide the other half in two vertically, and write the date 18 months ago in one half:
Now divide the remaining space in half, and write the date 18 months earlier (or in other words 3 years ago) in one half:
Repeat until your pen is thicker than the space you have to divide in two:
This demonstrates that your current computer is more powerful than all other computers you have had put together.
(You can use this diagram to demonstrate other things too).
For a computer person, living in recent decades has been a joy: computers keep getting cheaper and cheaper and more and more powerful.
At each ten-fold reduction in cost a new generation of computers has appeared which has made them more and more ubiquitous.
Now that computers have reached the €1 mark we can expect them to be used in just about every device you ever buy.