Internet and the Numbers


1988: 64Kbps
2019: Peaked at 6.7 Tbps
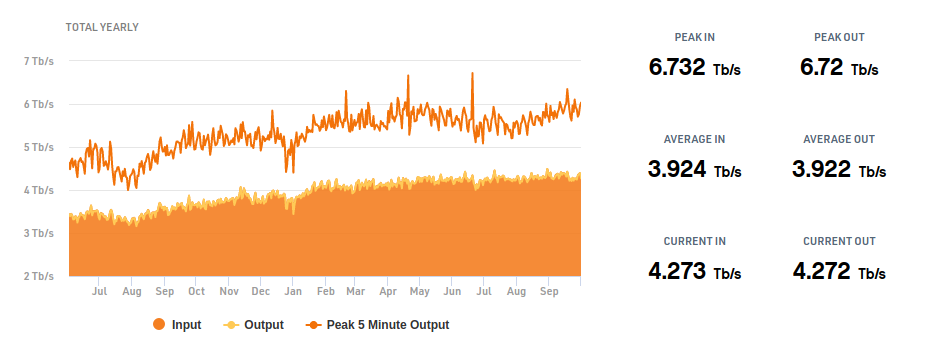
Over 100,000,000 times faster.
If the original internet speed was represented by a single pixel, there wouldn't be nearly enough pixels on this screen to represent the current speed.
Since 1988, the speed on the internet has doubled nearly 27 times; that's: 227
I bought a coffee and a cake for €5. The cake cost €2. How much was the coffee?
I bought two glasses of wine for €6. How much was one?
I bought a coffee and a cake for €5. The cake cost €2. How much was the coffee?
I bought two glasses of wine for €6. How much was one?
This just 'algebra', which we all can do in our heads.
a+b = 5
b = 2
a+2 = 5
a = 5−2
a = 3
Internet speed has increased 100M times over 30 years. How much has it increased per year?
New York Times:
LOS ANGELES — “The Interview” generated roughly $15 million in online sales and rentals during its first four days of availability, Sony Pictures said on Sunday.
Sony did not say how much of that total represented $6 digital rentals versus $15 sales. The studio said there were about two million transactions over all.
r = number of rentals; s = number of sales
r+s = 2M ("there were about two million transactions over all.")
6r+15s = 15M ("$6 rentals" "$15 sales" "generated $15M")
r+ s= 2M, so
6r+6s= 12M, so
6r = 12M−6s
6r+15s=15M, so
(12M−6s)+15s = 15M, so
15s−6s = 15M−12M, so
9s = 3M, so
s = ⅓M
r+s=2M, so
r = 2M−⅓M
r = 1⅔M
Numbers are abstractions.
There is no number 3 you can point to.
Numbers are ideas, all in our head.
French artist. 
Died on the battlefields of the First World War at the age of 23.
Was an artist for only 4 years and yet he is still considered one of the notable artists of the 20th century.
He claimed he could, without any training, read some Chinese.
Gaudier-Brzeska: "It just looks like a ..."
馬
Gaudier-Brzeska: "It just looks like a ..."
馬 Horse
Gaudier-Brzeska: "It just looks like a ..."
馬 Horse
駅 Train station
人
人 man
人 man
大
人 man
大 big
人 man
大 big
犬
人 man
大 big
犬 dog
人 man
大 big
犬 dog
木
人 man
大 big
犬 dog
木 tree
木 Tree
木 Tree
本
木 Tree
本 Book, wood
木 Tree
本 Book, wood
林
木 Tree
本 Book, wood
林 Grove, a wood
木 Tree
本 Book, wood
林 Grove, a wood
森
木 Tree
本 Book, wood
林 Grove, a wood
森 Forest
大 big
小 small
中 middle, medium
女 Woman
子 Child
子 Child
学
子 Child
学 School
子 Child
学 School
大学
子 Child
学 School
大学 University
日 Sun
月 Moon
日 Sun
月 Moon
明 light, bright
日 Sun
月 Moon
明 light, bright
10月5日 Today's date
木 Tree
日 Sun
東
木 Tree
日 Sun
東 East
木 Tree
日 Sun
東 East
日本 Japan
曜 weekday
日曜
月曜
曜 weekday
日曜 Sunday
月曜 Monday
火曜 Tuesday (Fireday)
水曜 Wednesday (Waterday)
木曜 Thursday (Treeday)
金曜 Friday (Goldday)
土曜 Saturday (Earthday)
山
山 Mountain
山 Mountain
火山
山 Mountain
火山 Volcano
王 King
王 King
玉 Jewel
王 King
玉 Jewel
国 Country
王 King
玉 Jewel
国 Country
中国
王 King
玉 Jewel
国 Country
中国 China (Middle land)
The 'reading age' for newspapers in the Netherlands and other western countries is 12.
That means: by the age of 12 you have enough education to read newspapers.
The reading age of Japanese newspapers is...
The 'reading age' for newspapers in the Netherlands and other western countries is 12.
That means: by the age of 12 you have enough education to read newspapers.
The reading age of Japanese newspapers is... 12
The 'reading age' for newspapers in the Netherlands and other western countries is 12.
That means: by the age of 12 you have enough education to read newspapers.
The reading age of Japanese newspapers is... 12
In other words, Japanese is no more difficult to read than Dutch or English.
While using 26 letters allows us to work out what a word is if we have never seen it before, in fact Japanese and Western readers read in the same way:
pattern recognition.
This also explains why weird English (and French) spelling is not important to them.
Should I set out on my autocycle? This was the question with which I began.I had a methodical mind and never set out on a mission withoutprolongedreflectionastothebestwayofsettingout.Itwasthefirstproblemtosolve,attheoutsetofeachenquiry,andInevermoveduntilIhadsolvedittomysatisfaction.SometimesItookmyautocycle,sometimesthetrain,sometimesthemotor-coach,justassometimestooIleftonfoot,oronmybicycle,silently,inthenight.Forwhenyouarebesetwithenemies,asIam,youcannotleaveonyourautocycle,eveninthenight,withoutbeingnoticed,unlessyouemployitasanordinarybicycle,whichisabsurd.
Should I set out on my autocycle? This was the question with which I began. I had a methodical mind and never set out on a mission without prolonged reflection as to the best way of setting out. It was the first problem to solve, at the outset of each enquiry, and I never moved until I had solved it to my satisfaction. Sometimes I took my autocycle, sometimes the train, sometimes the motor-coach, just as sometimes too I left on foot, or on my bicycle, silently, in the night. For when you are beset with enemies, as I am, you cannot leave on your autocycle, even in the night, without being noticed, unless you employ it as an ordinary bicycle, which is absurd.
Should I set out on my autocycle? This was the question with which I began. I had a methodical mind and never set out on a mission without prolonged reflection as to the best way of setting out. It was the first problem to solve, at the outset of each enquiry, and I never moved until I had solved it to my satisfaction. Sometimes I took my autocycle, sometimes the train, sometimes the motor-coach, just as sometimes too I left on foot, or on my bicycle, silently, in the night. For when you are beset with enemies, as I am, you cannot leave on your autocycle, even in the night, without being noticed, unless you employ it as an ordinary bicycle, which is absurd.
(From Molloy, by Samuel Beckett)
Aoccdrnig to a rscheearch at Cmabrigde Uinervtisy, it deosn't mttaer in waht oredr the ltteers in a wrod are, the olny iprmoetnt tihng is taht the frist and lsat ltteer be at the rghit pclae. The rset can be a toatl mses and you can sitll raed it wouthit porbelm. Tihs is bcuseae the huamn mnid deos not raed ervey lteter by istlef, but the wrod as a wlohe.
Accordion to scientific studies, 90% of the people do not realise that the beginning of this sentence has been replaced with an instrument.
So we use letters to learn a word, but after that we use pattern recognition.
Take as an example this: ¼
When you see this, you probably think immediately "one quarter", but it is in fact 'spelled' with three characters 1, /, 4, and 'means' "one divided by four".
There is no number 3 you can point to.
Numbers are ideas, all in our head.
We have to represent numbers in some way.
The Han character for three is: 三
Written by the Romans: III
And by us: 3
All three of them look more-or-less like three stripes.
In fact numbers probably started off being represented by tally stripes:
///
/////
Addition is easy: you put the stripes for one number next to the stripes for another, and count up the result:
//+/// = /////
We write addition as
a + b
There are a number of laws to do with addition.
The most obvious is called the commutative law:
a+b = b+a
Obviously //+/// = ///+//
Subtraction.
Subtraction.
This we can define as
(a+b)−b = a
This just says that subtraction undoes what addition does.
This definition of subtraction is declarative. It tells you the what but not the how.
At school we learn how to add, subtract, multiply, divide, but at a given point we are told:
The square root of n is the number r such that r × r = n
Simple, short, obvious, understandable, but few people know how to calculate one.
No problem because we have machines to do that for us.
We defined subtraction as (a+b)−b = a
But because of the commutative law
a+b = b+a
It's also true that
(a+b)−a = b
If I tell you that the sum of two people's age is 45, and one is 30, you know the age of the other.
In other words, you can extract either side of addition if you know the other number.
Subtraction isn't commutative:
2−3 ≠ 3−2
If I tell you the difference of two ages is 15, and one is 30, you don't know the age of the other.
In defining subtraction, something surprising has happened: new sorts of numbers have appeared.
We started with stripy numbers (what mathematicians call the counting numbers).
But now we can write calculations like:
0−5
How do you write these numbers down? What could they possibly mean?
Nowadays we are perfectly at home with negative numbers.
We understand what −5°C means, or that a negative speed means going backwards, or what it means to have €−100 in your bank account.
But in fact it took society, and even mathematicians centuries to properly accept negative numbers.
How could you have −5 sheep?
And 'plus' means 'more', yet 'adding' a negative number gives you less! What nonsense!
(These are actual arguments used)
If I say I have a square room of 36m², how long are the sides?
If I say I have a square room of 36m², how long are the sides?
Yes, 6m.
If I say I have a square room of 36m², how long are the sides?
Yes, 6m.
But −6m is also a good answer.
If I say I have a square room of 36m², how long are the sides?
Yes, 6m.
But −6m is also a good answer.
If you are now wondering, "How can a room have sides of −6m?" then you now understand how people used to feel about negative numbers.
(In fact a room can have sides of −6m, but I'm not going to show how now)
Through the ages people have written negative numbers in different ways:
But note: −5 is not a "negative number". It is an uncalculated operation, 'minus' applied to the positive number 5.
It is actually a shorthand for "0−5", where the 0 is invisible.
Even mathematicians don't agree: did subtraction define zero, or was it there all along?
Early in history zero wasn't counted as a number: if you didn't have any sheep, how could you say that you have a number of sheep?
Zero is the identity for addition (and subtraction):
a+0 = a
a−0 = a
There are also laws for negation, for instance
−−a = a
−(a−b) = b−a
The film Inception has worlds inside worlds.

At each level the world is recognisable, but has slight differences.
We're now about to enter the next inception level.
If I say "a×3", it means
a+a+a
Multiplication is defined in terms of the lower level.
Just like addition, multiplication is also commutative
a×b = b×a
Division.
Division.
We define it in exactly the same way:
(a×b)÷b = a
Like subtraction, division is not commutative:
3÷2 ≠ 2÷3
Since multiplication is commutative, just as with subtraction we can get both parts of a multiplication back:
(a×b)÷b = a
(a×b)÷a = b
Just like addition and subtraction, multiplication and division also have an identity: 1
a×1=a
a÷1=a
But although there is a shortcut for negation:
−a = 0−a
there isn't one for inversion.
But if we define it:
÷a = 1÷a
something surprising happens: we get exactly the same laws as with subtraction:
−−a = a
−(a−b) = b−a
For division:
÷÷a = a
÷(a÷b) = b÷a
When we entered the + inception world, we only had positive whole numbers, and subtraction created negative whole numbers.
Just as subtraction created new numbers, so does division:
We entered this world with positive and negative whole numbers, and division creates fractions (or rationals as mathematicians call them).
Yet these new numbers still work in the + world.

Just as multiplication is defined as repeated addition, raising to the power is defined as repeated multiplication:
a³ = a×a×a
However, I'd rather keep the notation consistent, so I will use an operator:
a↑3 = a×a×a
Something is different at this inception level though: ↑ is not commutative
2↑3 ≠ 3↑2
We define it in exactly the same way:
(a↑b )↓b = a
What does ↓ mean?
We define it in exactly the same way:
(a↑b )↓b = a
What does ↓ mean?
Root!
Which is traditionally -- and weirdly! -- written
b√a
↑ is not commutative
Which means that while
(a↑b)↓b = a
it is NOT the case that
✗ (a↑b)↓a = b ✗
So to get b we have to define another operator:
(a↑b)⇓a = b
What does ⇓ mean?
What does ⇓ mean?
Logarithm! Traditionally written
logb a
In other words:
If × is a 'higher' version of +, and ÷ is a higher version of −
Then ↑ is a 'higher' version of ×, and ↓ and ⇓ are just a higher version of ÷.
There are literally dozens of laws that look the same at this level:
You may know:
a½ = √a
Written new style this is:
a↑÷b = a↓b
which has an equivalent on the two layers down:
a×÷b = a÷b
a+−b = a−b

The world is filled with examples of things that grow with powers. E.g.:
(These are all taken from a 1960's book "Big Science, little science...and beyond, by Derek J. La Solla Price . Most of them I haven't checked against modern data)
Entries in dictionaries of national biography
Labour force
Population (I checked this one, and got 58 years)
Number of universities
Gross National Product (I got 10 years for UK 1955-2012)
Important discoveries
Important physicists
Number of chemical elements known
Accuracy of instruments
College entrants/1000 population
B.A., B.Sc.
Scientific journals
Membership of scientific institutes
Number of chemical compounds known
Number of scientific abstracts, all fields
Number of asteroids known
Literature in many scientific disciplines
Number of telephones in United States
Number of engineers in United States
Speed of transportation
Kilowatt-hours of electricity generated
Number of overseas telephone calls
Magnetic permeability of iron
Million electron volts of accelerators. (I checked the original data, and I got about 1.7 years. Redoing it with modern data, I get more or less exactly 2 years.)
You put an amount of money m in a savings account at an interest rate of 3%, then after ten years you will have
m×1.03↑10 (= €134 if you start off with €100)
Call the rate (1.03 in this case) r, and the number of years y:
m×r↑y
m×1.03↑10 = 1000
So divide both sides by 1.03↑10
m = 1000 ÷ 1.03↑10
which is €744
m×r↑10 = 2×m
Divide both sides by m
r↑10 = 2
take the 10th root of both sides:
(r↑10)↓10 = 2↓10
r = 2↓10
which is 1.072, in other words an interest rate of 7.2%
m×1.03↑y = 2×m
Divide both sides by m
1.03↑y = 2
and take the log of both sides
(1.03↑y)⇓1.03 = 2⇓1.03
y = 2⇓1.03
which is 23.45 (years)
Subtraction added negative numbers.
Division added fractions.
Did ↓ and ⇓ add any new numbers?
The pythagoreans were a religious sect based around mathematics. They believed that all numbers could be represented by fractions.
The story goes that one of their members, Hippasus, discovered that
2↓2 (the square root of 2)
couldn't be so represented.
The story continues that Hippasus was put to death, lest this information get out.
So ↓ introduces the irrational numbers.
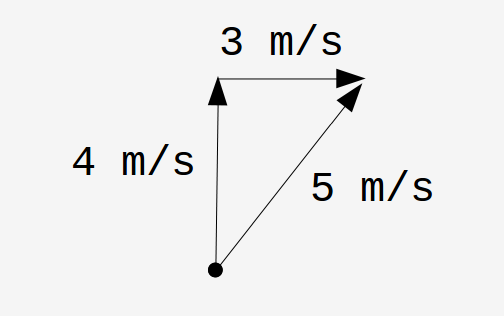
Imagine you are sailing a motor boat at 4 m/s with the stream of a river flowing at 3 m/s.
Then if I watch from the river bank, you appear to be travelling at
(4 + 3) = 7 m/s
However, if you are travelling against the stream, then your speed is 4 m/s, and the river is −3 m/s. So you appear to me to be travelling at
(4 + −3) = 1 m/s
One way to show addition is to draw lengths
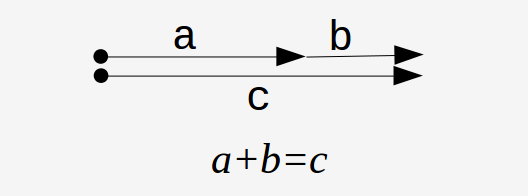
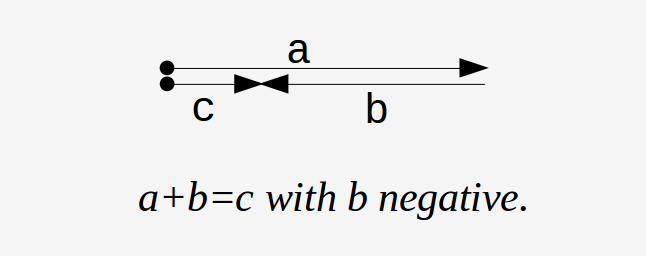
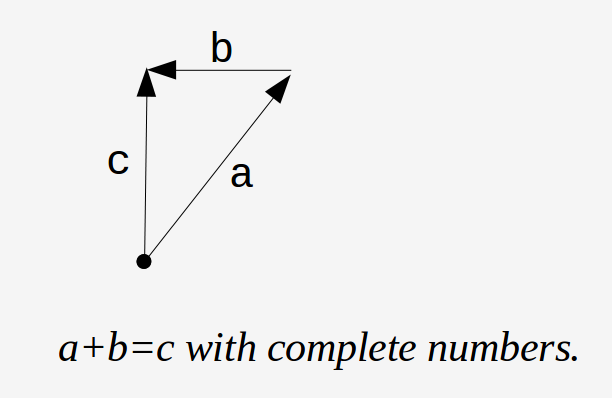
These new numbers still work in the +, × worlds as well as the ↑ world where they come from.
Mathematicians call 3 a 'real' number, 4 an 'imaginary' number and 5 a 'complex' number.
You can see why I prefer to call them 'complete' numbers.
The worlds of computer speeds and internet speeds seem amazing, with their constant doubling.
In fact doublings like that happen in lots of places.
With very simple arithmetic you can work out all sorts of interesting information.
The internet in the Netherlands has grown from 64K bps in 1988 to 6.7T bps in 2019. What's the yearly growth?
64k × g↑31 = 6.7T
g↑31 = 6.7T ÷ 64k
(g↑31)↓31 = (6.7T ÷ 64k)↓31
g = 1.81
So the annual growth rate is 81%
The doubling period is
1.81↑y = 2
(1.81↑y)⇓1.81 = 2⇓1.81
y = 1.16
1.16 years is about 1 year, 1 month and 28 days.