Programmers are humans too:
On the design of notations
Steven Pemberton, CWI, Amsterdam

ME
ME
= Maine
Looking at GA= Georgia, and FL= Florida, it appears that there is no real rule.
Looking at GA= Georgia, and FL= Florida, it appears that there is no real rule.
What I could work out is:
NE: Nevada or Nebraska?
NE: Nevada or Nebraska?
It's Nebraska, but NB would have been a better choice
NE: Nevada or Nebraska?
It's Nebraska, but NB would have been a better choice
MI: Mississippi, Missouri, Michigan, or Minnisota?
NE: Nevada or Nebraska?
It's Nebraska, but NB would have been a better choice
MI: Mississippi, Missouri, Michigan, or Minnisota?
It's Michigan, but MG would have been a better choice
NE: Nevada or Nebraska?
It's Nebraska, but NB would have been a better choice
MI: Mississippi, Missouri, Michigan, or Minnisota?
It's Michigan, but MG would have been a better choice
MS: Mississippi, Missouri, or Minnisota?
NE: Nevada or Nebraska?
It's Nebraska, but NB would have been a better choice
MI: Mississippi, Missouri, Michigan, or Minnisota?
It's Michigan, but MG would have been a better choice
MS: Mississippi, Missouri, or Minnisota?
It's Mississippi, but MP would have been a better choice.
But solving these problems with reading 2-letter codes would still not solve the problem of writing them: your passive and active abilities are different.
I couldn't believe it wasn't possible to do the 2-letter codes better.
So I wrote a program (in ABC as it happens; more on that later).
The best rule I came up with:
My point here is that the 2-letter codes were introduced because of automation.
But that is no excuse for ignoring the needs of people.
The fact is, people are strange, yes even you, even me.
For instance, someone did research in whether tools affected how people wrote.
The fact is, people are strange, yes even you, even me.
For instance, someone did research in whether tools affected how people wrote.
The fact is, people are strange, yes even you, even me.
For instance, someone did research in whether tools affected how people wrote.
The fact is, people are strange, yes even you, even me.
For instance, someone did research in whether tools affected how people wrote.
Research into interfaces for playing chess:
Research into interfaces for playing chess:
Mouse was by far the fastest
Research into interfaces for playing chess:
Mouse was by far the fastest
But with direct manipulation, people won more often...
Hold your hand up.
Count the number of triangles on the next screen, and check your result.
Drop your hand when you have counted.
but count the red shapes.
Usability is about designing things (software/programming languages/cookers) to allow people to do their work:
Efficient, Error-free,
Enjoyable or
Fast, Faultless and Fun
Don't confuse usability with learnability: they are distinct and different.
The problem is that the people designing things are usually not the people who will be using those things, and they tend to design for themselves.
So... you have to use HCI techniques:
No one really talks seriously about the usability of notations.
The design of notations affects what you can do with them.
The ease of manipulation with numbers is greatly dependent on the nomenclature we have chosen for them -- Dijkstra
For instance, Roman numerals:
CXXVIII+CXXVIII
=CCXXXXVVIIIIII
=CCXXXXVVVI
=CCXXXXXVI
=CCLVI
I was helping my children with their maths homework, and a question arose for me:
Why do they make things so difficult?
So I went back to first principles.
What follows was more than a year's work, using reams of paper. It is hard work making things simple. It resulted in a monograph that I wrote for my sons' birthdays. You can read it here: Numbers.
As a colleague who designs program interfaces complained: "When you succeed in making an interface as easy to use as a coffee machine, they treat you like a plumber"
We'll use base 1 numbers: // is 2, /// is 3
We define addition as sticking two numbers together:
//+///=/////
We define subtraction as
(a+b) − b = a
This is a declarative definition. It tells you the what but not the how.
Because addition is commutative:
(a+b) = (b+a)
you can use subtraction to obtain both the left and right operands of addition:
(a+b) − a =
(b+a) − a = b
Subtraction creates a new sort of number we didn't start with, since we have expressions now like
3 − 5
the result of which we can't write with stripes.
Negative numbers upset mathematicians right up into the 19th century, being referred to as "fictitious" solutions.
Even banks didn't start using negative numbers until recently.
Whether subtraction also introduces zero, or whether it was there from the start is something mathematicians disagree on to this day.
At least historically though, it wasn't originally considered a number.
Zero is the identity for addition and subtraction since
(a+0) = a
We also have a monadic version of − as a shorthand:
−a = 0 − a
(It was from Dijkstra that I first learned this, but I cannot at the moment find the reference)
We go up a level, and define multiplication in terms of addition:
a × 3 = a + a + a
and it also has an identity value:
a×1 = a
(That was handwaving; the true definition of multiplication is:
(a + b) × c = a×c + b×c
It still defines multiplication in terms of addition.)
We define division in exactly the same way as we did with subtraction:
(a×b) ÷ b = a
And since multiplication is also commutative, you can extract both a and b in the same way as we did with subtraction.
(I use ÷ instead of / because when user-testing with my target audience, they said "Please use the same symbols as on a calculator".)
Division adds the rationals to the mix, since we now have numbers such as
2÷3
(We may represent such numbers as ⅔, but we should recognise this as just an uncalculated expression, just as −5 is)
Oddly, there is no monadic version of divide. But if we define it using the same pattern:
÷a = 1 ÷ a
something surprising happens: identities that we know from the lower level have exactly the same form as ones at this level. For instance:
−−a = a
÷÷a = a
a−−b = a + b
a÷÷b = a × b
−(a−b) = (b−a)
÷(a÷b) = (b÷a)
(This shows that while subtraction and division aren't commutative, they are commutable.)
Just as multiplication is defined as repeated addition, so is raising to the power defined as repeated multiplication:
a↑3 = a × a × a
One difference at this level: ↑ is not commutative:
2↑3 ≠ 3↑2
Which means it has two complements, one to give a and one to
give b.
First for a, which uses our regular pattern:
(a↑b)↓b = a
This is of course what we know of as root, where x↓y traditionally, and weirdly, is notated
y√x
Now we need b:
(a↑b)⇓a = b
This is logarithm, where x⇓y is equally weirdly notated traditionally as
logy x
So if ↑ is a higher version of multiplication, then ↓ and ⇓ are just higher versions of division.
Apart from making the close relationship between root and log obvious, defining them in this way suddenly exposes that literally dozens of well known identities have a similar form to identities at the two lower levels!
Just to pluck a few out:
a×(−b) = −(a×b)
a×(−b) = −(a×b)
a↑(−b) = ÷(a↑b)
a×(−b) = −(a×b)
a↑(−b) = ÷(a↑b)(a−b = 1/ab)
a×(÷b) = a÷b
a×(÷b) = a÷b
a↑(÷b) = a↓b
(I consider this so beautiful, that even if this had been the only result, the whole exercise would have been worth it!)
a×(÷b) = a÷b
a↑(÷b) = a↓b(a1/b = b√a)
÷(a÷b) = b÷a
÷(a÷b) = b÷a
÷(a⇓b) = b⇓a
÷(a÷b) = b÷a
÷(a⇓b) = b⇓a(1/ logba = logab)
(I may have learned this at school, but if I did, I had forgotten it. When I saw this result, I was so amazed, that even though I could prove it, I have to admit I checked it with some values as well, to make sure it was right).
⇒ Consistent
⇒ Easier to use (once you've learnt it)
⇒ Exposes otherwise hidden relationships, such as the close relationship between log and root.
⇒ Use the same methods for solving equations:
a+2 = 4
a = 4−2a × 2 = 4
a = 4 ÷ 2a↑2 = 4
a = 4↓22↑a = 4
a = 4⇓2
A most important, but also most elusive, aspect of any tool is the influence on the habits of those who train themselves in its use. If the tool is a programming language, this influence is -- whether we like it or not -- an influence on our thinking habits. -- Dijkstra
Imagine, hypothetically, that programmers are humans...despite all evidence to the contrary:
Imagine, hypothetically, that programmers are humans...despite all evidence to the contrary:
Imagine, hypothetically, that programmers are humans...despite all evidence to the contrary:
Imagine, hypothetically, that programmers are humans...despite all evidence to the contrary:
Imagine, hypothetically, that programmers are humans...despite all evidence to the contrary:
Imagine, hypothetically, that programmers are humans...despite all evidence to the contrary:
Also pretend, just for a moment, that their chief method of communicating with a computer was with programming languages.
Imagine, hypothetically, that programmers are humans...despite all evidence to the contrary:
Also pretend, just for a moment, that their chief method of communicating with a computer was with programming languages.
What should you do?
We designed a programming language: ABC
We used the HCI principles:
ABC went on to form the basis of Python.

Just one of 21 cabinets making up the computer.

The first computer so cheap that they gave it away on the cover of a magazine
The Elliot ran for about a decade, 24 hours a day.
How long do you think it would take the Raspberry Pi Zero to duplicate that amount of computing?
The Elliot ran for about a decade, 24 hours a day.
How long do you think it would take the Raspberry Pi Zero to duplicate that amount of computing?
The Raspberry Pi Zero is about one million times faster...
The Raspberry Pi is not only one million times faster. It is also one millionth the price.
A factor of a million million.
A terabyte is a million million bytes: nowadays we talk in terms of very large numbers.
Want to guess how long a million million seconds is?
The Raspberry Pi is not only one million times faster. It is also one millionth the price.
A factor of a million million.
A terabyte is a million million bytes: nowadays we talk in terms of very large numbers.
Want to guess how long a million million seconds is?
30,000 years...
A really big number...
In fact a million million times improvement is about what you would expect from Moore's Law over 58 years.
Except: the Raspberry Pi is two million times smaller as well, so it is much better than even that.
When a new technology is introduced, it is often priced not on what it costs to produce, but based on what it costs to do the same with the technology it is replacing.
For example, when Edison first introduced electric light into homes, electricity was priced based on what it would cost to produce the same amount of light by traditional means, but now with additional benefits of instant light, and no flames.
Similarly, early computers were priced based on what it would cost to do the same amount of computation using people.
In the 50's, computers were so expensive that nearly no one bought them, but leased them.
To rent time on a computer then would cost you of the order of $1000 per hour: several times the annual salary of a programmer!
When you leased a computer you would get programmers for free to go with it.
Compared to the cost of a computer, a programmer was almost free.
The first programming languages were designed in the 50s:
Cobol, Fortran, Algol, Lisp.
They were designed with that economic relationship of computer and programmer in mind.
It was much cheaper to let the programmer spend lots of time producing a program than to let the computer do some of the work for you.
Programming languages were designed so that you tell the computer exactly what to do, in its terms, not what you want to achieve in yours.
It happened slowly, almost unnoticed, but nowadays we have the exact opposite position:
Compared to the cost of a programmer, a computer is almost free.
I call this Moore's Switch.
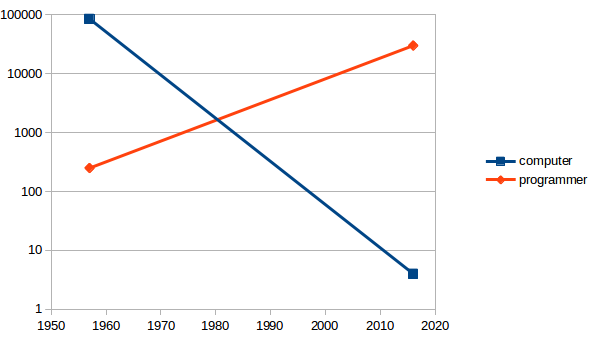
Relative costs of computers and programmers, 1957-now
But, we are still programming in programming languages that are direct descendants of the languages designed in the 1950's!
We are still telling the computers what to do.
A new way of programming: declarative programming.
This describes what you want to achieve, but not how to achieve it..
Let me give some examples
Declarative approaches describe the solution space.
A classic example is when you learn in school that
The square root of a number n is the number r such that r × r = n
This doesn't tell you how to calculate the square root; but no problem, because we have machines to do that for us.
function f a: {
x ← a
x' ← (a + 1) ÷ 2
epsilon ← 1.19209290e-07
while abs(x − x') > epsilon × x: {
x ← x'
x' ← ((a ÷ x') + x') ÷ 2
}
return x'
}
This is why documentation is so essential in procedural programming.
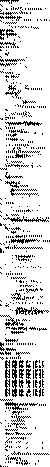
1000 lines, almost all of it administrative. Only 2 or 3 lines have anything to do with telling the time.
And this was the smallest example I could find. The largest was more than 4000 lines.
type clock = (h, m, s) displayed as circled(combined(hhand; mhand; shand; decor)) shand = line(slength) rotated (s × 6) mhand = line(mlength) rotated (m × 6) hhand = line(hlength) rotated (h × 30 + m ÷ 2) decor = ... slength = ... ... clock c c.s = system:seconds mod 60 c.m = (system:seconds div 60) mod 60 c.h = (system:seconds div 3600) mod 24
XForms is a declarative system for defining applications. 
It is a W3C standard, and in worldwide use.
A certain company makes one-off BIG machines (walk in): user interface is very demanding — traditionally needed:
5 years, 30 people.
With XForms this became:
1 year, 10 people.
Do the sums. Assume one person costs 100k a year. Then this has gone from a 15M cost to a 1M cost. They have saved 14 million! (And 4 years)
Manager: I want you to come back to me in 2 days with estimates of how long it will take your teams to make the application.
Manager: I want you to come back to me in 2 days with estimates of how long it will take your teams to make the application.
[Two days later]
Programmer: I'll need 30 days to work out how long it will take to program it.
Manager: I want you to come back to me in 2 days with estimates of how long it will take your teams to make the application.
[Two days later]
Programmer: I'll need 30 days to work out how long it will take to program it.
XFormser: I've already programmed it!
The British National Health Service started a project for a health records system.
The British National Health Service started a project for a health records system.
One person then created a system using XForms.
XForms is all about state. (Which means it meshes well with REST - Representational State Transfer).
Initially the system is in a state of stasis.
When a value changes, by whatever means, the system updates related values to bring it back to stasis.
This is like spreadsheets, but much more general.
The result is: programming is much easier, since the system does all the administrative work for you.
I've got a position in the world as x and y coordinates, and I want to display the map tile of that location at a certain zoom.
My data:
x, y, zoom
Openstreetmap has a REST interface for getting such a thing:
http://openstreetmap.org/<zoom>/<x>/<y>.png
However, the Openstreetmap coordinate system changes at each level of zoom.
As you zoom out, there are in each axis half as many tiles, so there are ¼ as many tiles. And the interface indexes tiles, not locations.
So to get a tile:
The data: x, y, zoom
scale = 226 - zoom
tilex = floor(x/scale)
tiley = floor(y/scale)
url = concat("http://tile.openstreetmap.org/", zoom, "/", tilex, "/", tiley, ".png")
That is really all that is needed (modulo syntax, which looks like this:)
<bind ref="tilex" calculate="floor(../x div ../scale)"/>
That's the form. Now the content:
<input ref="zoom" label="zoom"/> <input ref="x" label="x"/> <input ref="y" label="y"/> <output ref="url" mediatype="image/*"/>
and the tile will be updated each time any of the values change.
For historical reasons, present programming languages are at the wrong level of abstraction: they don't describe the problem, but only one particular solution.
Declarative programming allows programmers to be ten times more productive: what you now write in a week, would take a morning; what now takes a month would take a couple of days.
Once project managers realise they can save 90% on programming costs, they will switch to declarative programming.
I believe that eventually everyone will program declaratively: fewer errors, more time, more productivity.