A new job
You've been offered a new job in Rotterdam.
But since you like your house in Amsterdam, and don't fancy looking for a
new house, you decide to commute by train.
But that means you will need a bike to get to the train station, and since
you are not allowed to take bikes on the train in the rush hour, you'll have to
get one for in Rotterdam as well, and you'll also have to find somewhere to
park it there.
You know what? Folding bikes are allowed in trains in the rush
hour, so you decide to buy one.
Requirements
First you make a list of what you want from a folding bike. It must be:
- light
- strong
- cheap, or at least affordable
- easy to fold and unfold
- quick to fold and unfold
- compact when folded
- comfortable to ride
- ...
There are probably a dozen such properties that you want a folding bike to
fulfil.
Constraints
Well, let’s just take three of them: light, strong, and cheap.
Unfortunately, search as you may, you won’t be able to find a folding
bike that matches all three:
- you can find strong and light, but not cheap;
- you can find cheap and strong, but not light;
- you can find cheap and light, but not strong.
Just those three constraints are not satisfiable.
You could find strong, cheap and light, but then it wouldn’t
be a bike: being a bike and being foldable are two constraints that are
non-negotiable – it must be a bike, and it must be
foldable.
Negotiation
So in other words, you will have to relax at least one of your negotiable
constraints.
- You could decide not to go on holiday next year and use that extra money
to buy a non-cheap bike.
- You could decide to put up with a heavy bike.
- You could decide to be careful, and go with a fragile bike.
In any case, you're going to have to put up with non-perfection.
The perfect partner
You shouldn’t expect to find a perfect partner either. What might you
want in a partner?
- good looking
- healthy
- fit
- financially secure
- amusing
- good conversationalist
- good natured
- good at cooking
- musical
- good in bed
- ...
There are lots of possible constraints, and they will be different for
different people.
Non-negotiable
Then there are probably a few that you wouldn’t think of mentioning,
maybe because they are non-negotiable, like:
- of the gender you are interested in
- in an age group not too different from your own
- speaks a language that you also speak
- interested in you
and so on, and so on.
People
The problem is, as you add each constraint, the pool of potential perfect
partners gets smaller and smaller.
And then you have to add the constraint that it is someone you will actually
get to meet in a social context...
This is why you should prepare yourself for not meeting the perfect
partner: you need to relax some of your constraints to find someone who is at
least satisfactory.
Music
Which brings us, funnily enough, to music.
Notes
You probably know that a note in music is caused by air vibrating, at a
different frequency for different notes.
For instance, internationally it has been agreed that the note A above
middle C has a frequency of 440Hz.
Frequencies
When we say that a tone is a frequency, what that means is that very rapidly
the air is compressed and decompressed: once every
1/440th of a second for the note A. Typically we draw it
like this:
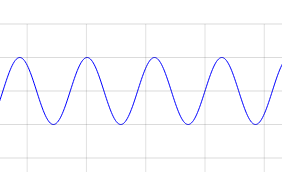
The distance between each peak is 1/440th of a second;
a peak shows the maximum compression, and a trough the minimum.
Ears
If we play two notes simultaneously, it turns out that our ears like
combinations of frequencies that are related in certain simple ways, as small
ratios of frequencies.
Pythagoras apparently discovered this.
For instance, a note played an octave higher is just twice the frequency,
that is to say they have a ratio of 2:1.
So the A one octave higher would be 880Hz.
| A |
A# |
B |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
| 440 |
|
|
|
|
|
|
|
|
|
|
|
880 |
|
|
and the A an octave lower would be 220Hz.
We hear a note an octave higher as almost the same note, only 'higher'.
Demonstration
So let's look at some combinations
of tones.
What you'll see is that when you play two tones together, their compressions
interact: they get added together.
If at a given moment they both have the same compression, you get twice the
compression as a result. If one is compressed and the other decompressed, they
cancel each other out.
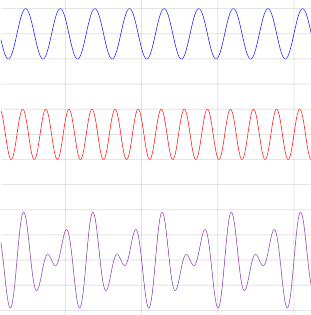
Noise cancelling
In fact this is how noise-cancelling headphones work: they take the sounds
you are hearing and play the opposite compression to into your ear so that they
cancel each other out.
Difference
When you play two tones together, you also hear the note that is the
difference between the two frequencies.
You can best hear this by playing two notes very close to each other, such
as 220Hz and 221Hz. You will hear a beat of 1Hz.
If you change it to 220Hz and 222Hz, you hear two beats a second, and so
on.
This is the best way to tune an instrument: you play two (nearly) identical
notes, and change one until you don't hear the beat any more.
Fifths
After 2:1, the next-most simple ratio of frequencies is 3:2.
This is classically the relationship between the notes called a
“perfect fifth”, between the first note on the major scale, and the
fifth (which are seven semitones apart).
So for instance, a fifth from A is the note E, so E should have a frequency
of 440 × 3÷2, which is 660Hz.
| A |
A# |
B |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
| 440 |
|
|
|
|
|
|
660 |
|
|
|
|
880 |
|
|
Octave
Of course, we want to be able to play a perfect fifth from any note, not
just A, so the perfect 5th from E, which is B, would have a frequency of 660 ×
3÷2, which is 990 Hz.
| A |
A# |
B |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
| 440 |
|
|
|
|
|
|
660 |
|
|
|
|
880 |
|
990 |
Since 990 is above 880, we can halve the number to take it down into the
octave we are building up, between 440Hz and 880Hz. So the B is at 495Hz.
| A |
A# |
B |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
A# |
B |
| 440 |
|
495 |
|
|
|
|
660 |
|
|
|
|
880 |
|
990 |
Next
The fifth above that is F# which will have a frequency of 742.5:
| A |
A# |
B |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
| 440 |
|
495 |
|
|
|
|
660 |
|
742.5 |
|
|
880 |
Scale
And so we can build up a whole octave based on the premise that from every
note we can also play the perfect fifth and step through C#, G#, D#, A#, F, C,
G, up to D, which has a frequency of 594.7Hz.
| A |
A# |
B |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
| 440 |
469.9 |
495 |
528.6 |
556.9 |
594.7 |
626.5 |
660 |
704.8 |
742.5 |
792.9 |
835.3 |
880 |
The fifth above that takes us back to A, which will have a frequency of
594.67 × 3÷2, which is ... 892 Hz? But shouldn't A be 880Hz?
Yes it should.
Bells
In other words, it is impossible to make an octave of notes where you can
play a perfect 5th from every other note.
This is how the bells of the Westerkerk are tuned, for instance, and this
tuning has been used in music for hundreds of years.
They didn't know how to solve the problem of the 'Wolf tone', and so, as the
bellringer of Amsterdam says "There are some scales you just can't use".
A solution
It is clear hopefully that the octaves are non-negotiable. Any solution has
to have the octave of any note as twice the frequency, otherwise you would get
awful dissonance.
So maybe we can loosen our other constraints.
The solution was first discovered by the great Flemish mathematician and
scientist, Simon Stevin.
We replace our constraint with: divide the octave up into 12 equal steps,
equal in the sense that each semitone has the same frequency ratio with its
neighbour. But what is that ratio?
Ratio
Let’s call the ratio r.
Starting from A, the calculation 440×r should give us A#.
Then A#×r should give us B. This is the same as 440×r×r
Then 440×r×r×r should give us C, and so on all the way up to the next A:
440×r×r×r×r×r×r×r×r×r×r×r×r = 880 (that’s twelve r’s).
Ratio
Writing this another way:
440×r12 = 880
or
r12 = 880÷440
or
r12 = 2
or in other words
r = 12√2
Well, we know how to calculate that: r is just under 1.06.
Result
So if we calculate the resultant octave, it looks like this:
| A |
A# |
B |
C |
C# |
D |
D# |
E |
F |
F# |
G |
G# |
A |
| 440 |
466.2 |
493.9 |
523.3 |
554.4 |
587.3 |
622.3 |
659.3 |
698.5 |
740 |
784 |
830.6 |
880 |
You can see that for E where the ideal 5th from A would be 660, that the
difference is very small, less than 1Hz.
In other words, all notes, except the octave, are very slightly out of tune,
but the difference is so small that since we want to hear the right
tuning, we think it is properly tuned (amusingly, this is a lack of dissonance
due to cognitive dissonance).
Conclusion
So, the conclusion is, don’t expect perfection, but if you relax some
of your requirements you might just find something that so nearly matches that
you can’t tell the difference.

