AI and XForms

Steven Pemberton, CWI, Amsterdam

Why AI

We try to get a computer program to act like a human.

Or maybe even better

Knowledge

We build up knowledge by observation, identifying patterns, and learning.

Encoding knowledge

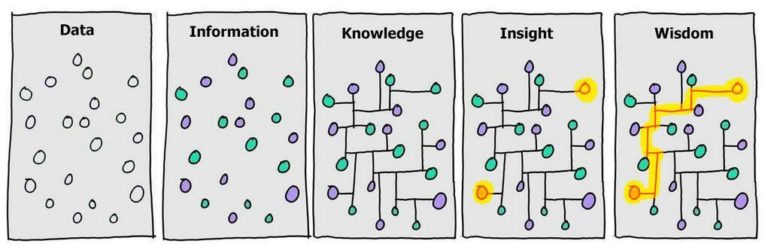
If we want programs to behave like humans, we need methods of encoding knowledge.

Let's take an example.

Noughts and Crosses/Tic Tac Toe

I imagine everyone here can play it perfectly.

Encode rules:

• If you are about to win, take that move
• If you are about to lose, block that move
• If you own a position in an otherwise empty line, take another position in that line.

Etc ...

Another approach

Surprisingly, there are only 765 possible (legal) board positions, because of symmetries.

For instance, these 4 are all the same:

X

		X

		X

X

Symmetries

These 8 are all the same:

X		O

X
O

O		X

		X
		O

O		X

		O
		X

O
X

X		O

Encoding knowledge

So we take each of the 765 boards, and then record which move we would do from that position.

Now we have an encoding of our knowledge of noughts and crosses, and the program can use that to play against an opponent.

Yet another approach: learning

Again enumerate all 765 boards

Link each board with its possible follow-on boards. For instance, for the empty board (the initial state) there are only three possible moves:

to

	X

X		X
X		X

	X
X		X
	X

Second move

From the centre position start move, there are only two possible responses:

	X

to

O		O
	X
O		O

	O
O	X	O
	O

Second move

From the corner position start move there are five responses:

X

to

X
	O

X
		O

X	O
O

X		O
O

X
		O
	O

Second move

From the edge first move there are also five responses:

X

to

X	O

X		O

O
X
O

	O
X
	O

		O
X
		O

And so on

So we have linked all possible board situations to all possible follow-on positions.

Give each of those links a weight of zero.

Learning program

Play the computer against itself:

Repeatedly make a randomly chosen move from the current board until one side wins, or it's a draw.

When one side has won, add 1 to the weight of each link the winner took, and subtract one from each link the loser took. (Do nothing for a draw)

Then repeat this, playing the game millions of times.

Use the program

Playing against a human, when it's the program's turn, from the current board position make the move with the highest weight.

Generalising

Rule based systems:

Generalised rules

Condition → Consequence
Condition → Consequence
Condition → Consequence

A consequence may have an effect on other conditions, making those true, and therefore generating more consequences, effectively chaining rules together.

Generalised learning

Current AI techniques try to emulate how brains work, by simulating neurons.

Neuron

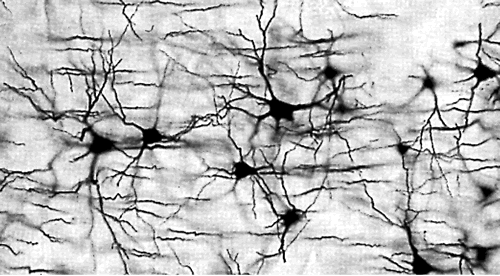
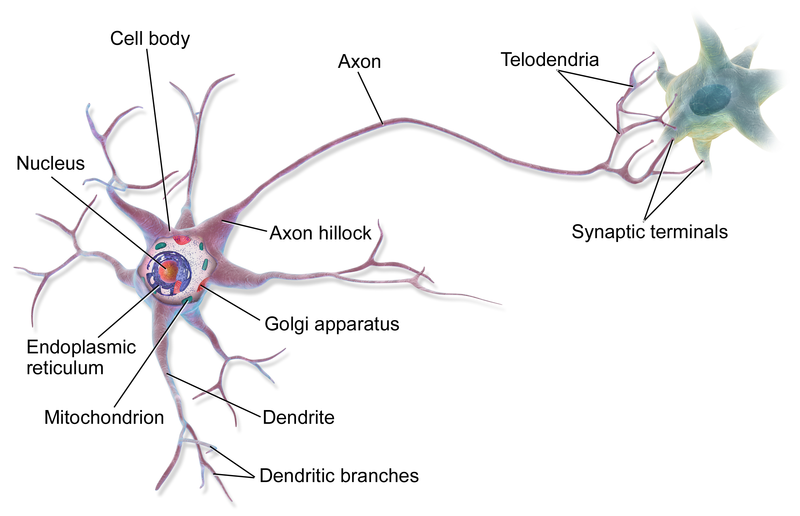
A neuron has a number of inputs (the dendrites) and a single output (the axon) which connects to other neurons via synapses.

BruceBlaus, CC BY 3.0, via Wikimedia Commons

Simulated neurons

In the simulation, a neuron has a number of (binary) inputs, each carrying a weight. The products of each input and its weight are summed to give a value. If this value exceeds a certain threshold, the neuron fires, setting its output to 1.

(We know that this is Turing complete, since you can model a computer using only NAND neurons with two inputs and one output).

Networks

There are two types of network that are used:

• feed forward: no loops
• recurrent (or feedback): with loops - neurons can have input from itself or later neurons.

Feed forward

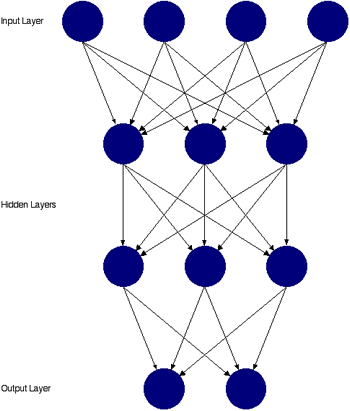
Feed forward networks are static - they produce a consistent output for a set of inputs. They have no time-based memory: previous states have no effect.

Feedback

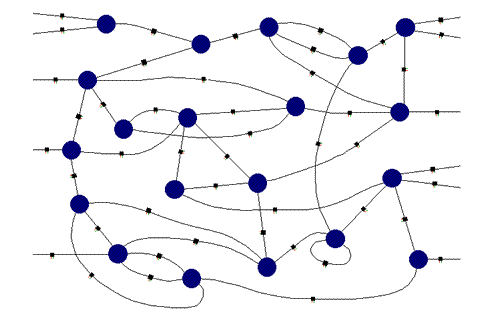
Feedback networks are dynamic. The network has time-based states.

Learning

Since we have binary inputs and binary outputs, the knowledge is in the weights assigned to the inputs.

Initially random weights are assigned.

There is a large set of training data giving the outputs you should get for particular data.

This data is put through the system, adjusting the weights in order to get the required outcomes.

There are many variants of algorithms for adjusting weights, and I am not going to present them here.

Using

Once the weights have been calculated on the training data, then the network can be used for analysing new data.

Advantages

The advantage of learning systems vs encoded knowledge systems, is that the learning systems may spot things we weren't aware of.

The disadvantage is that we can no longer determine why it produces a result that it does. It becomes an unanalysable black box.

Dangers

A danger of both the encoded knowledge and the learning system is that they can both end up encoding bias.

A rule-based encoding system is going to end up encoding the encoder's bias.

A learning system is going to end up representing the bias implicit in the teaching data.

XForms

Invariants

Essential mechanism within XForms.

Relationships are specified between values: if a value changes, for whatever reason, its dependent values are changed to match.

This may then generate a chain of changes along dependent values.

Similar to spreadsheets, but: much more general.

Example: Map Application

Source

Map

About 90 lines of XForms.

Not a single while statement.

Dijkstra in his seminal book A Discipline of Programming first pointed out that the principle purpose of a while statement in programming is to maintain invariants.

It is then less surprising that if you have a mechanism that automatically maintains invariants, you have no need for while statements.

How it works

High-level abstraction: there is a two-dimensional position of a location in the world, and a value for the magnification or zoom value required; a map is maintained centred at that location.

It uses a service that delivers (square) map tiles for a region covering a set of locations at a particular zoom level:

http://<site>/<zoom>/<x>/<y>.png

Tiles

The coordinate system for the tiles is as a two-dimensional array.
At the outermost level, zoom 0, there is a single tile

Tiles

At the next level of zoom, 2×2 tiles,

Tiles

At the next level 4×4, then 8×8, and so on, up to zoom level 19.

Calculation

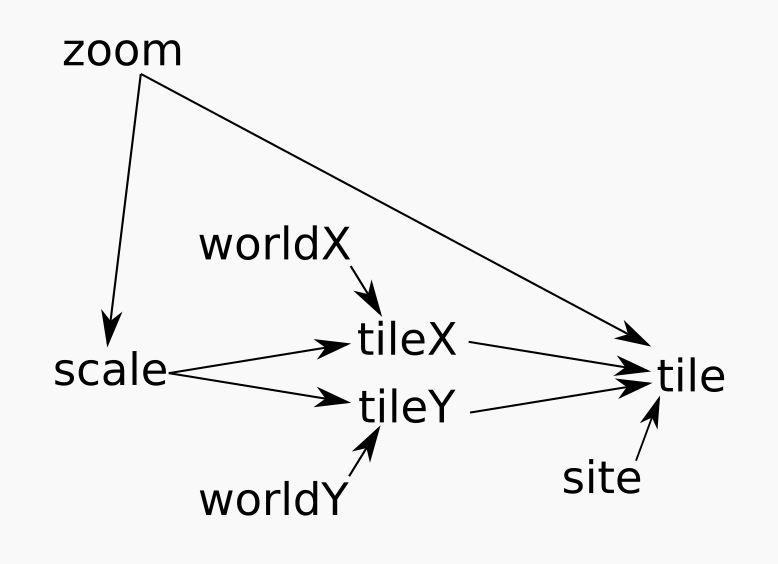
For the tile for a location in world coordinates, calculate from the zoom how many locations are represented by each tile, and divide:

scale=2^{26 - zoom}
tile_x=floor(world_x ÷ scale)
tile_y=floor(world_y ÷ scale)

In XForms:

<bind ref="scale" calculate="power(2, 26 - ../zoom)"/>
<bind ref="tileX" calculate="floor(../worldX div ../scale)"/>
<bind ref="tileY" calculate="floor(../worldY div ../scale)"/>

These are not assignments, but invariants – statements of required equality: if zoom changes then scale will be updated. If scale or worldX changes, then tileX will be updated, and so on.

Tile

It is equally easy to calculate the URL of the tile:

<bind ref="tile"
      calculate="concat(../site, ../zoom, '/',
                        ../tileX, '/', ../tileY,
                        '.png')"/>

and displaying it is as simple as

<output ref="tile" mediatype="image/*"/>

For a larger map, it is easy to calculate the indexes of adjacent tiles.

So displaying the map is clearly easy, and uses simple invariants.

Panning

Making the map pannable uses the ability of keeping the mouse coordinates and state of the mouse buttons as values.

When the mouse button is down, the location of the centre of the map is the sum of the current location and the mouse coordinates.

As this value changes, so the map display is (automatically) updated to match.

Advantages

The advantages of the invariant approach:

• Specify intent
• Computational intent much more obvious
• Computer does more of the work
• Much shorter code
• Faster production time

Implementation

XForms uses a straightforward ordered-graph based dependency algorithm, ordered since circular dependencies are disallowed.

Updates are triggered by changes to values, and updates are then ordered along the dependency chain and applied.

Networks

So guess what:

XForms already has the inherent mechanism for simulating neuron networks.

Although the XForms system uses a feed-forward network, it is possible to simulate a feed back network.

Feed forward

If I have a value n, and another value that is some guess at the square root of that value, then the expression

((n ÷ g) + g) ÷ 2

will give a better approximation of the square root.

I'm not going to prove this, you'll have to accept my word for it.

(Non-binary) neuron

So I can create an XForms neuron

<instance>
   <data xmlns="">
      <value>2</value>
      <result/>
   </data>
</instance>

<bind ref="result"
      calculate="((../value div preceding-sibling::*) + preceding-sibling::*) div 2"/>

Feed forward example

Each time you click on the arrow, it adds another neuron to the system, getting you closer to the square root

Source

All the arrow does is add another element to the instance. XForms does the rest:

 <trigger>
    <label>→</label>
    <action ev:event="DOMActivate">
       <insert ref="result"/>
    </action>
 </trigger>

Feedback version

Here the only change is that instead of adding a new element, when the button is clicked, the result is copied back to the approximation.

<trigger>
   <label>→</label>
   <action ev:event="DOMActivate">
      <setvalue ref="approx" value="../result"/>
   </action>
</trigger>

Source

Mechanism

So XForms has in-built the mechanism needed to implement neural networks.

<instance>
   <neuron value="" threshold="" xmlns="">
      <in value="" weight=""/>
      <in value="" weight=""/>
      <in value="" weight=""/>
      <out/>
   </neuron>
</instance>

<bind ref="neuron/in/@value"
      calculate=".. * ../weight"/>
<bind ref="neuron/value"
      calculate="sum(../in/@value)"/>
<bind ref="neuron/out"
      calculate="if(../value &gt; ../threshold, 1, 0)"/>

AI Workbench