The ABC Programmer's Handbook by Leo Geurts, Lambert Meertens, and Steven Pemberton
This chapter gives a semi-formal definition of ABC. It describes the syntax and semantics of ABC, and lists the predefined commands, functions and predicates.
ABC has two basic types of values: numbers and texts, and three ways of making new types of values from existing ones: compounds, lists and tables. Texts, lists and tables have in common that they contain an arbitrary length progression of 'items', all of the same type. They are collectively known as trains.
All values of a given type have an ordering, which means that all values of the same type can be compared with each other. This ordering is informally specified below; for a precise definition see section Order tests. Comparison of values of different types is not allowed. All values have a textual representation, and can be written and read.
The built-in functions of ABC for operating on values are described in section Formulas with predefined functions. Several of these functions are defined for trains in general.
Numbers come in two kinds:
exact and approximate.
Exact numbers are rational numbers. For example, 1.25 = 5/4, and (1/3)*3 = 1 . There is no restriction on the size of numerator and
denominator. An exact number with a denominator of 1 is referred to
as an integer.
Approximate numbers are implemented by whatever the hardware or software has to offer for fast but approximate arithmetic (floating point).
The
arithmetic operations and many other functions give an exact result
when their operands are exact, and an approximate result otherwise,
but the function sin, for example, always
returns an approximate number.
An exact
number can be made approximate with the ~
function (e.g. ~1.25); the functions exactly, round, floor and ceiling can be
used to convert an approximate number to an exact one. Exact and
approximate numbers may be mixed in arithmetic, as in 4 * arctan 1, and in comparisons, as in sin x > 0 .
A text (string) is composed of
printable ASCII characters, its items. Texts are variable length, and are
ordered in the usual lexicographic way: "a" <
"aa" < "b" . There is no separate type 'character': a single character is in fact
again a text, of length one.
The printable characters are the 95
characters represented below, where the blank space preceding '!' stands for the (otherwise invisible) space
character:
!"#$%&'()*+,-./0123456789:;<=>?
@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_
`abcdefghijklmnopqrstuvwxyz{|}~
The ordering on the characters is the ASCII collating order, which is the order in which the characters are displayed above.
A
compound consists of a sequence of values, its fields. For example, the number 3 and the text "xyz" may be
combined to give the compound 3, "xyz" .
Compounds are also ordered lexicographically, For example (3, "xyz") < (3, "yz") < (pi, "aaa") .
For this to be meaningful, the compounds that are compared must be of the same type. This means that they have the same number of fields, and that corresponding fields are of the same type.
The only way to obtain the individual fields of a compound is to put it in a multiple-location with the right number of components, as in
PUT name IN last.name, first.name, middle.name
A list is a sorted sequence of
values, its items. All
items of a list must be of the same type, and this determines the
type of the list. The length of a list may vary without influencing
its type. When a new item is inserted in a list (with an INSERT command), it is automatically inserted in
the list in the proper position in the sorting order. A list may
contain duplicates of the same item. Items may be removed with the
REMOVE command. Again, lists themselves are
ordered lexicographically.
A table consists of a (sorted)
sequence of table entries.
Each table entry is a pair of two values: a key and an associated value, the
corresponding item, and the
sorting of the entries in the table is on the keys. The ordering of
tables is again lexicographic. All keys of a table must be of the
same type; similarly, all table items must also be of the same type
(but that type may be different from that of the keys). A table may
not contain duplicate keys. If k is a key of the table t, then t[k]
selects the corresponding item. New entries in a table can be made,
or the item of existing entries modified, by putting a new item
value in the table after selecting with the key value, as in
PUT a IN t[k]. Entries can be deleted with the DELETE command, as in
DELETE t[k]. When a table is used as a train, only its items count,
and its keys are irrelevant, but the order of the items in the
train is the same as that of the entries, which are in the order of
the sorted keys.
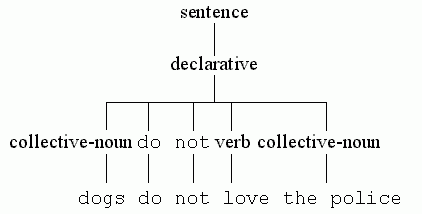
The syntax of ABC is given in the form of a collection of rules. Each rule is displayed in a box and starts with the name of the thing being defined followed by a colon; following this, one below the other, are one or more alternatives, each clearly marked with a • in front. Each alternative is composed of symbols that stand for themselves, or the names of other rules. These other rules are then defined elsewhere in the grammar, or possibly in the same rule.
Occasionally, a syntax rule is explained in English, rather than formally. Italic font is used for such an explanation.
As an example, here is a simple grammar for a small part of English:
sentence:
, connective sentencedeclarative:
do not verb collective-nouncollective-noun:
catsdogspeoplethe policeverb:
lovehateeathassleconnective:
andbutalthoughbecauseyetThe first rule of this modest grammar states that each sentence is either a declarative, whatever that may be, or a declarative followed by a comma-sign followed by a connective followed by another sentence. What a declarative is, follows from the next rule, and so on, until only symbols remain which need no further explanation. So, one possible sentence can be obtained as follows:

Other sentences that can be produced with the grammar are:
the police hassle dogs cats do not hate cats , but cats hate dogs , because dogs hate cats people eat dogs , yet dogs love people
You will
notice that the names of rules are in another typeface than words
like eat that stand for themselves. In the grammar of ABC that
follows, furthermore, rule names are all in lower-case letters,
while words that stand for themselves, with one exception, are all
in upper-case letters, so they are easily distinguished. The one
exception is the letter e in the exponent part of a numeral in
section Numerals.
It often happens that a part of an alternative is optional. There is a special template rule serving for all these cases:
optional-whatever:
empty:
(Empty produces nothing.)
The 'optional' rule is included to save many rules in the definition, and stands for rules like:
optional-comment:
If a name is used in a rule whose definition is to be found in another section, then name is a link to the definition in that other section. For instance the rule above indicates that the rule for comment is to be found in another section (the section on Representations).
new-line:
ABC program texts consist of indented lines. A new-line-proper marks a transition to a new line. An indent stands for the left margin blank offset. Initially, the left margin has zero width. The indentation is increased by an increase-indentation and decreased again by a decrease-indentation. These always come in pairs and serve for grouping, just as begin-end pairs do in other programming languages. An increase-indentation is always preceded by a line ending with a colon (possibly followed by comment).
comment:
\ optional-comment-bodyComments may be placed at the end of a line or may stand alone on a line where a command may otherwise stand. No comment may precede the first line of a how-to (see section How-to's).
comment-body:
Example comment:
\ modified 6/4/84 to reject passwords of length < 6
Lines are constructed from signs organised into symbols, keywords, names, numerals, and other symbols.
keyword:
A point in a keyword must not be followed by another point, nor be the last sign of the keyword.
keyword-suite:
Example keywords: keyword-suites:
PUSH PUSH CAN'T.DO CAN'T DO UPSIDE UPSIDE DOWN A.3'B
name:
Example names:
push can't.do a.3'b"
Most
other symbols consist of single signs, but some are composite: ..,
**, */, /*, ^^, <<, ><, >>, <=, <> and
>=.
Spaces
are freely allowed between symbols, but not within keywords, names,
numerals and composite symbols. Sometimes spaces are required to
separate keywords and names from following symbols. For example,
cos y is not the same as cosy: the latter is taken to be one
name.
How-to's are the building blocks of an ABC 'program'. You can define new commands, functions and predicates by writing a how-to. These how-to's reside in a workspace.
how-to-script:
A name used as an address of a location (a variable) in a how-to is by default private (local) to that how-to. This means that if the same name is used as an address outside the how-to, it refers to a different location. So the location for a private name is only accessible during the invocation of the how-to. It is therefore a temporary location that ceases to exist at the end of the invocation. If a location should be shared between several how-to's, or should otherwise survive the invocation in which it is created, either it should be passed as a parameter, or the name should be listed in a share-command (section SHARE) at the start of the how-to-script, in which case it then stands for a shared (global) name of the workspace. The location of a shared name is created as 'permanent', meaning that it survives, together with its contents, even on logging out. The shared names with the contents of their locations are also called the 'permanent environment'. There is one permanent environment corresponding to each workspace.
The invocation of a function- or predicate-how-to cannot alter the contents of permanent locations or delete them, or create new permanent locations, in any way such that the changes survive after the invocation of the how-to (in other words, such how-to's cannot have 'side-effects'). If such a how-to appears to modify the contents of a shared name, it effectively modifies a private 'scratchpad' copy and the change is invisible after the invocation of the how-to.
A command-how-to defines the meaning of a new command (see section User-defined commands for how to invoke them). Once the command has been defined, it may be used in the same way as the built-in commands of ABC. The execution of the command then invokes the how-to, whose script specifies what actions must be taken for executing the command. Other user-defined commands may be used in the script of a how-to when writing it, even if they have not yet been defined, though they must be defined by the time the how-to is invoked.
command-how-to:
HOW TO command-template:command-template:
The
first keyword-suite of a command-template must be unique, i.e.,
different from the first keyword-suites of all predefined and other
user-defined commands. So it is impossible to redefine the built-in
commands of ABC. Additionally, the very first keyword of the suite may not be CHECK,
HOW, IF, REPORT, RETURN or WHILE.
Otherwise, it may be chosen freely. There are no restrictions on the second and further keyword-suites.
template-trailer:
template-parameter:
Example command-how-to:
HOW TO PUSH value ON stack:
PUT value IN stack[#stack+1]
See also: User-defined commands .
A function-how-to defines the meaning of a new function (see section Formulas with user-defined functions for how to invoke them).
Functions are used in formulas (section Formulas) which are a special case of expressions. The first line of a how-to defining a new function contains a so-called formula-template, which contains the name of the function being defined. Formulas may be zeroadic (no operands), monadic (one operand following the function name) or dyadic (two operands surrounding the function name). A function-how-to is invoked upon the evaluation of a formula and returns a value, which is supplied with the return-command (section RETURN).
function-how-to:
HOW TO RETURN formula-template:formula-template:
zeroadic-formula-template:
monadic-formula-template:
dyadic-formula-template:
Function names must not be 'overloaded' (multiply defined). However, a given name may be used at the same time for a dyadic function and a monadic function.
template-operand:
Example function-how-to:
HOW TO RETURN (a, b) over (c, d):
PUT c*c+d*d IN rr
RETURN (a*c+b*d)/rr, (-a*d+b*c)/rr
A predicate-how-to defines the meaning of a new predicate (see section Examinations with user-defined predicates for how to invoke them). Predicates are used in examinations, which are a special case of tests. Like functions, predicates may be zeroadic, monadic or dyadic.
Tests do not return a value, but succeed or fail via the report, succeed and fail commands.
predicate-how-to:
HOW TO REPORT examination-template:examination-template:
zeroadic-examination-template:
monadic-examination-template:
dyadic-examination-template:
Like functions, predicate names must not be 'overloaded', though a given name may be used at the same time for a dyadic predicate and a monadic predicate.
Example predicate-how-to:
HOW TO REPORT a subset b:
REPORT EACH x IN a HAS x in b
See also: REPORT; SUCCEED; FAIL; Examinations with user-defined predicates .
Refinements support the method of 'top-down' programming, also known as programming by 'stepwise refinement'. When writing a how-to, the specification of commands, expressions and tests may be deferred by referring them to refinements that reflect the appropriate coarse-grained level of the algorithm. These refinements are then specified at the end of the how-to, and may themselves be refined to the necessary detail, possibly in several steps. As with how-to's, there are three kinds of refinements. The differences with how-to's are:
refinement-suite:
refinement:
command-refinement:
The
keyword-suite of a command-refinement must be different from the
first keyword-suites of all predefined commands, and of all other
command-refinements in the how-to. It may, however, be the same as
the first keyword-suite of a user-defined-command. Additionally,
the very first keyword of
the suite may not be CHECK, HOW, IF, REPORT, RETURN or WHILE.
Example command-refinement:
SELECT TASK:
PUT min tasks IN task
REMOVE task FROM tasks
expression-refinement:
Example expression-refinement:
stack.pointer:
IF stack = {}: RETURN 0
RETURN max keys stack
test-refinement:
Example test-refinement:
special.case: REPORT position+d = line.length
See also: Refined commands; Refined expressions; Refined tests.
Commands may be given as 'immediate commands', interactively from the keyboard, or may be part of a how-to. If commands are given as immediate commands, they are obeyed directly: any names used as addresses in the command are then interpreted as shared names from the permanent environment. Within a how-to, address names are private, unless they have been listed in a share-command (see section SHARE).
If the interrupt key is pressed while a command is executing, or a run-time error is reported, execution is aborted, and the user is prompted for another immediate command.
command:
simple-command:
terminating-command:
control-command:
command-suite:
Command-suites are used in the bodies of how-to's, refinements, and control-commands. A command-suite may only follow the preceding colon on the same line if it is a simple-command. Otherwise, it starts on a new line, with all lines of the command-suite indented.
command-sequence:
Example command-suite:
IF name in keys abbrev.table:
PUT abbrev.table[name] IN name
IF name not.in name.list:
INSERT name IN name.list
The commands of a command-suite are executed one by one, until the last one has been executed or until a terminating command (see section Commands) is executed.
The execution of the command-suite of a function-how-to or expression-refinement must end in a return-command, and return-commands may only occur within such command-suites.
The execution of the command-suite of a predicate-how-to or test-refinement must end in a report-, succeed- or fail-command, and these may only occur within such command-suites.
Share-commands are used to import shared names into a how-to.
SHARE namingA share-command may only occur as the first command of a how-to, or immediately after another share-command.
Example share-command
SHARE name.list, abbrev.table
The names of the naming are taken as names of non-local permanent locations. Whenever the names are located during the invocation of the how-to, these permanent locations are used instead of temporary locations private to the how-to.
Check-commands are used to check that a condition is satisfied. They may be used, for example, to check the requirements of parameters or operands on invoking a how-to. The liberal use of check-commands helps to get programs correct quickly.
check-command:
CHECK testExample check-command:
CHECK i >= 0 AND j >= 0 AND i+j <= n
When a check-command is executed, its test is performed. If the test fails, an error is reported and the currently executing immediate command is aborted. Otherwise, no message is given and execution continues.
Put-commands are the assignment commands of ABC.
put-command:
PUT expression IN addressExample put-command:
PUT a+1, ({}, {1..a}) IN a, b
The value of the expression is put in the location of the address, which means that a copy of the value is stored there. If no such location exists already, one is created on the spot. The value will be held in that location until a different value is put in the location, or the location is deleted. It can be inspected again by just naming the right address. The types of the value and the location must agree (though this is currently not always checked).
If the location is created locally (the name did not occur in an immediate command and was not listed in a share-command), the location will cease to exist when the current how-to is exited. If a location already existed for the name, its old contents are superseded by the new value.
If a
value is put in a
multiple-location, the value must be a compound with as many fields
as there are single-locations in the multiple-location. The
successive fields are then put in the successive single-locations.
It is an error in such a 'multiple put' if it makes a difference in
what order the fields are put in the single-locations (as in
PUT 1, 2 IN x, x where the final value of x might be either 1 or 2).
Note that
the meaning of
PUT a, b IN b, a is well defined (provided that a
and b are defined and have values of the same type): first the
value of the expression
a, b
is determined, and then that value is
put in
b, a. Note also that the meaning of
PUT t[i], t[j] IN t[j], t[i]
is well defined, even if i and j have the same value. For
although in this case a value is put twice in the same location,
that value is the same each time, so the order does not matter.
This definition of putting a value in a location is also used by read-commands, for-commands, user-defined-commands, user-defined-functions and -predicates, and quantifications.
Write-commands are used to write values on the screen. All values in ABC may be written.
output-format:
single-expression-sequence:
, single-expression-sequenceExample write-commands:
WRITE // WRITE count[k], "times", k /
Each single-expression, if any, is evaluated and converted to a text and written on the screen. Each / causes a transition to a new line on the screen. Note that you write no comma before or after the /'s.
The value of each single expression is converted to a text according to the syntax of single-expression (section Expressions) unless it is a text, when it is converted without surrounding quotes. Adjacent single-expressions are written separated by a space, unless they are texts. Thus,
WRITE 0, 1, "!", 2, "x", "y", 3, ("x", "y") /
gives
0 1 ! 2 xy 3 ("x", "y")
and
WRITE "Yell" WRITE "ow!" /
gives
Yellow!
For
formatting purposes, see the operators
>>,
<<, and
><
(section Functions on values of all types), the function round (section
Functions on numbers) and the conversions in text-displays (section Text displays).
Read-commands are used to read input from the user. Values of any type can be read.
input-format:
Example read-commands:
READ x EG 0 READ (n, s) EG (0, "") READ message[#message+1] RAW
The execution of a read-command prompts the user to supply one input line.
With an EG format, the input is interpreted as an expression of the same type as the example expression following EG. (Usually, the example expression will consist of constants, but other expressions are also allowed.) The input expression is evaluated in the permanent environment (so private names of how-to's cannot be used) and put in the location of the single-address. To input a text-display (literal), text quotes are required.
If a RAW format is specified, the single-address must be a text address. The input line is put in the location of the address literally. No text quotes are needed.
Set-random-commands are used to start or re-start the random sequence used for the functions random (see Functions on numbers) and choice (see Functions on trains). They can be used, for instance, to make the results from programs using these functions reproducible.
set-random-command:
SET expressionExample set-random-command:
SET RANDOM "Monte Carlo", run.nr
The random sequence used for the functions random and choice is reset to a point depending on the value of the expression (how this is done is not further specified). Each ABC-session starts this sequence at some random point.
Remove-commands are used to remove an item from a list.
remove-command:
REMOVE expression FROM addressExample remove-command:
REMOVE task FROM tasks
The location of the address must hold a list, and the value of the expression must be an item of that list. The item is removed. If it was present more than once, only one instance is removed.
Insert-commands are used to insert an item in a list.
insert-command:
INSERT expression IN addressExample insert-command:
INSERT new.task IN tasks
The location of the address must hold a list. The value of the expression is inserted as a list item. If that item was already present, one more instance will be present.
Delete-commands are used to delete locations, including those of table entri es and other (non- text-selection) addresses such as unwanted shared names and their locations.
delete-command:
DELETE addressExample delete-command:
DELETE t[i], u[i, j]
The
location for the address ceases to exist. If a multiple-address is
given, all its single-addresses are deleted. If a
table-selection-address is given, the table must contain the key
that is used as selector. The table entry with that key is then
deleted from the table. It is an error to delete a
text-selection-address (e.g., t@2).
Note that the meaning of
DELETE t[i], t[j]
is well defined, even if i and j
have the same value.
A pass-command serves to provide a dummy filling for a command-suite (which may not be empty) in case no action is needed. This is mainly useful in select-commands, but also for the scripts of how-to's still under construction.
Example pass-command:
PASS
The execution of a pass-command entails no action.
Example of the use of a pass-command:
SELECT:
too.small: ENLARGE
too.large: REDUCE
just.fine: PASS
A quit-command is used for terminating the invocation of command-how-to's or command-refinements, or to terminate an ABC session.
A quit-command may only occur in the command-suite of a command-how-to or command-refinement, or as an immediate command.
Example quit-command:
QUIT
The execution of a quit-command causes the termination of the invocation of the command-how-to or command-refinement in whose command-suite it occurs. The execution of the invoking user-defined- or refined-command is thereby terminated and further execution continues as if the invoking command had terminated normally.
Given as
an immediate command, QUIT terminates the current session. All
how-to's and shared names with their locations in the permanent environment
survive and can be used again at the next session.
Return-commands are used to terminate the invocation of a function-how-to or expression-refinement , and return a value.
return-command:
RETURN expressionReturn-commands may only occur within the command-suite of a function-how-to or expression-refinement.
Example return-command:
RETURN (a*c+b*d)/rr, (-a*d+b*c)/rr
The execution of a return-command causes the termination of the invocation of the function-how-to or expression-refinement in whose command-suite it occurs. The value of the expression is returned as the value of the invoking formula or refined-expression.
Report-commands are used to terminate the invocation of a predicate-how-to or test-refinement, reporting success or failure.
report-command:
REPORT testReport-commands may only occur within the command-suite of a predicate-how-to or test-refinement.
Example report-command:
REPORT i in keys t
The
execution of a report-command causes the termination of the
invocation of the predicate-how-to or test-refinement in whose
command-suite it occurs. The invoking examination or refined-test
succeeds/fails if the test of the report-command succeeds/fails. If
the invoker is a test-refinement, any bound names set by a for-command (see
section FOR), or a
quantification (section Quantifications), will temporarily survive, as described under
REFINED-TESTS (section Refined tests). The command 'REPORT test' is equivalent to
SELECT:
test: SUCCEED
ELSE: FAIL
A succeed-command is used to terminate the invocation of a predicate-how-to or test-refinement, reporting success.
Succeed-commands may only occur within the command-suite of a predicate-how-to or test-refinement.
Example succeed-command:
SUCCEED
The execution of a succeed-command causes the termination of the invocation of the predicate-how-to or test-refinement in whose command-suite it occurs. The invoking examination or refined-test succeeds. As with report-commands, bound names temporarily survive.
The
command SUCCEED is equivalent to REPORT 1 = 1.
A fail-command is used to terminate the invocation of a predicate-how-to or test-refinement, reporting failure.
Fail-commands may only occur within the command-suite of a predicate-how-to or test-refinement.
Example fail-command:
FAIL
The execution of a fail-command causes the termination of the invocation of the predicate-how-to or test-refinement in whose command-suite it occurs. The invoking examination or refined-test fails. As with report-commands, bound names temporarily survive.
The
command FAIL is equivalent to REPORT 1 = 0.
These are commands defined by a how-to.
user-defined-command:
trailer:
actual-parameter:
The keywords and actual-parameters must correspond one to one to the keywords and template-parameters of the command-template of one unique command-how-to in the current workspace.
Example user-defined-commands:
CLEAN UP DRINK me TURN a UPSIDE DOWN PUSH v ON operand.stack
A user-defined-command is executed in the following steps:
The execution of the user-defined-command is complete when the execution of the command-suite terminates (normally, or because of the execution of a quit-command) and the address positions as described above have been dealt with.
The effect of this parameter passing is as follows: Actual-parameters that are expressions, and expressions contained in an actual-parameter that is an address, are evaluated once, at the entry of the how-to. During the execution of the how-to-script, the template-parameters serve as private names. Only upon completion are values that were put in template-parameters in the course of execution passed back to the actual-parameters. If the execution is aborted by a user-interrupt or because of an error, the actual-parameters will not be affected. Changes to shared names from within the how-to-script, however, take effect immediately.
An example of a call of a how-to that is not allowed due to restriction 6 above is
HOW TO FILL HALF OF a, b:
PUT 0 IN b
PUT {} IN table
FILL HALF OF table[1]
Note that in contrast to function- and predicate-how-to's, changes to the template-parameters will be passed back to the actual-parameters of a command, so that they cannot be used as working storage for intermediate calculations.
See also: Command how-to's; QUIT .
These are used to execute commands defined in command-refinements.
refined-command:
The keyword-suite of a refined-command must occur as the keyword-suite of one command-refinement in the how-to in which it occurs. That command-refinement specifies the meaning of the refined-command.
Example refined-command:
REMOVE MULTIPLES
A refined-command is executed by executing the command-suite of the corresponding command-refinement. The execution of the refined-command is complete when the execution of this command-suite terminates (normally, or because of the execution of a quit-command).
See also: command-refinement (in Refinements); QUIT .
If-commands are used to conditionally execute a command-suite depending on the success of a test. If something should be executed on failure too, or there are more alternatives, a select-command should be used.
if-command:
IF test :Example if-command:
IF i < 0: PUT -i, -j IN i, j
The test is performed. If it succeeds, the command-suite is executed; if it fails, the command-suite is not executed.
The
command 'IF test: command-suite' is equivalent to:
SELECT:
test: command-suite
ELSE: PASS
See also: SELECT .
Select-commands are used to conditionally execute one out of a number of command-suites depending on the success of associated tests.
alternative-suite:
alternative-sequence:
single-alternative:
else-alternative:
ELSE :Example select-commands:
SELECT: SELECT:
a < 0: RETURN -a a < 0: RETURN -a
a >= 0: RETURN a ELSE: RETURN a
The tests
of the alternatives are performed one by one, starting with the
first and proceeding downwards, until one is found that succeeds.
The corresponding command-suite is then executed. ELSE may be used
in the final alternative as a test that always succeeds. If all the
tests fail, an error is reported.
While-commands are used to execute a command-suite repeatedly, depending on the success of a test.
while-command:
WHILE test :Example while-command:
WHILE x > 1: PUT x/10, c+1 IN x, c
If the test succeeds, the command-suite is executed. If the execution of the command-suite terminates normally, the test is performed a second time, and if it succeeds, the command-suite is executed again, and next the test is performed again, and this alternation continues until the test, when performed, fails, or until an escape is forced by a terminating-command. If the test fails the very first time, the command-suite is not executed at all.
For-commands are used to repeat a command-suite once for each item of a train.
for-command:
FOR ranger :ranger:
IN expressionExample for-commands:
FOR i IN {1..10}: WRITE i, i**2 /
FOR k IN keys t: WRITE k, ":", t[k] /
FOR i, j IN keys t: PUT t[i, j] IN t'[j, i]
The value of the expression must be a train. One by one, each item of that train is put in the location of the naming, and each time the command-suite is then executed. For example,
FOR c IN "ABC": WRITE "letter is ", c /
is equivalent to
WRITE "letter is ", "A" / WRITE "letter is ", "B" / WRITE "letter is ", "C" /
If t is a
table, then 'FOR a IN t: TREAT a' treats the table items of t in
the same way as
FOR k IN keys t:
PUT t[k] IN a
TREAT a
Note that the expression of a for-command is evaluated once. Altering the value of the expression within the command-suite does not alter how often the command-suite is executed. A premature exit can be forced, however, by a terminating command.
The names of the naming of a for-command are 'bound-names', and may not be used outside of the command-suite to which they are bound. There is one exception to this rule: if a for-command is used in a test-refinement, and within the for-command a report-, succeed- or fail-command is executed, the currently bound names will temporarily survive as described under REFINED-TESTS (section Refined tests).
See also: namings (in Addresses); Quantifications .
An expression is evaluated to give a value. The evaluation of an expression cannot alter the contents of locations that currently exist, nor can it delete locations or create new locations that survive the expression. If an expression appears to alter a location, it effectively modifies a private 'scratchpad' copy, and the change is invisible outside the expression.
expression:
basic-expression:
simple-expression:
tight-expression:
( expression
)Example basic-: simple-: tight-expressions:
a a a
-a
a+b (a+b)
The various kinds of expressions that are distinguished here serve to define the syntax in such a way that no parentheses are needed when the meaning is sufficiently clear.
If in a given context some name could be interpreted as a simple-expression - that is, as the name of a (shared or private) location, or of a refinement - and as a zeroadic formula - when it is the name of a zeroadic function - the interpretation as a simple-expression takes precedence.
For example, the command PI defined by
HOW TO PI:
PUT 4 IN pi
WRITE pi
outputs 4 and not 3.14159...
Example multiple-expressions:
1, "abc" (1, 0), (0, 1), (-1, 0), (0, -1)
The value of a multiple-expression composed of single-expressions separated by commas is the compound whose fields are the values of the successive single-expressions.
numeral:
integral-part:
digit:
Example numerals
666 3.14 2.99793e8 2.99793e+8 1e-9
The value
of a numeral is an exact number. For example, 1.25 stands for the
exact number 5/4. The exponent-part, if present, gives the power of
ten with which the value of the fixed-notation has to be
multiplied. For example, 1.2345e2 has the same value as
1.2345*10**2, which is the same number as 123.45.
There are
no notations for negative or approximate constants. However, the
formula -1.2345e2 may take the role of a 'negative constant', and, likewise, the
formula ~1.2345e2 serves as an 'approximate constant'.
address-inspection:
The value of an address-inspection is the value last put in the location created for the name which is the address-inspection. The location must already exist and hold a value.
Table-selections are used to obtain an item from a table.
table-selection:
Example table-selections:
t[i, j]
{["yes"]: 1; ["no"]: 0}[answer]
The value of the tight-expression must be a table T and the value of the expression between the square brackets must be a key K of T. The value of the table-selection is then the item of the table entry in T whose key is K
Train-displays are used to express values for trains.
train-display:
The text-displays '' and "" stand for the empty text.
In a text-display in the ' ... ' style, any single quote ' in the text must be written twice to give ''. Otherwise, it would signal the end of the text-display. Similarly, in a text-display in the " ... " style, any double quote " in the text must be written twice to give "". Finally, in either style of text-display, the back-quote ` must also be written twice, giving ``. Otherwise, it signals a conversion.
The
quotes and conversion-signs that have to be written twice according
to these rules correspond to one character of the resulting text. For
example, the number of characters in 'x''y""z' is 6, because it
consists of one x, one ' character, one y, two " characters, and
finally one z. Another way to specify the same text is
"x'y""""z".
conversion:
` expression ` The
requirement that some signs be written twice does not hold inside a
conversion. For example, '`t['a']`' is proper,
whereas '`t[''a'']`' is not.
Example text-displays:
'' 'He said: "Don''t!"' "He said: ""Don't!""" 'altitude is `a/1e3` km'
The value of a text-display is the text composed of the characters given between the enclosing text quotes. If the text-display contains conversions, the expressions of these conversions are evaluated first and converted to a text in the same way as for a write-command. For example, since
WRITE 239*4649
causes the text 1111111 to be written, the text-display
"239 times 4649 gives `239*4649`"
is equivalent to
"239 times 4649 gives 1111111"
list-filler:
The ambiguity in, e.g., {1...9},
is resolved by interpreting it as {1. .. 9}.
Example list-displays:
{}
{x1; x2; x3}
{1..n-1}
{"a".."z"; "0".."9"; "."; "'"; '"'}
The value
of {} is an empty list.
(It may also be an empty table; see below.)
The value of a list-display containing list-fillers is the list whose items are the values of those list-fillers. If values occur multiply, they give rise to multiple items in the list.
For a list-filler of the form p..q, p and q must both be integers, or both be characters (texts of length one). The values of the list-filler are then all integers or characters x such that p ≤ x ≤. For example,
{1..4} = {1; 2; 3; 4} and
{"A".."C"; ": OK"} = {"A"; "B"; "C"; ": OK"}
If p > q, the
list-filler has no values. For example, {5; 7..4} = {5}.
Note that
the expressions in a list-display need not be in the order of their
values. For example, {3; 2; 1} is allowed and has the same value as
{1..3}.
All items of a list must have the same type.
table-filler:
[ expression ] : single-expressionExample table-displays:
{}
{[i, j]: 0}
{[0]: {}; [1]: {0}}
{[name]: (month, day, year)}
The
table-display {} stands for an empty table. Otherwise, each table-filler
gives a table entry with
key K and item I where K
is the value of the expression between square brackets, and I is
the value of the single-expression following the colon. The result
is then the table containing these table entries.
If there are different table entries with the same key, an error is reported. Multiple occurrences of the same table entry, however, are allowed. The extra occurrences are then simply discarded.
All keys of a table must have the same type. Similarly, all items must have the same type, but not necessarily the same type as the keys.
zeroadic-formula:
monadic-formula:
dyadic-formula:
zeroadic-function:
monadic-function:
~
+ - */ /* # namedyadic-function:
+
- * / ** ^ ^^ | @ # << >< >> nameactual-operand:
The parsing ambiguities in these rules are resolved by priority rules, as follows:
1 + sin x), or the order makes
no difference (as in a*b*c, a*b/c, or a^b^c), no parentheses are needed.~ and monadic + monadic and dyadic # ** monadic - * and / dyadic + and - @ and | ^^ ^ /* and */ names <<, >< and >>
sin or floor), and the functions
/* and */, may only be used having formulas as operands or in
operands of higher-priority formulas if these operands are
parenthesised (but not in, e.g., exp abs x, because of point 1
above, or in 5 round sin x >> 8 because of point 1 and
>> having a lower priority). Because
of rule 1 both a/b/c and a/b*c are ambiguous. Because of rule 3 sin x+y is ambiguous. Each of these can be made correct by inserting
parentheses, depending on the intention: either (a/b)/c or a/(b/c),
either (a/b)*c or a/(b*c),
and either (sin x) + y or sin(x+y).
Note that because of rule 3, sin(x)+1 is just as wrong as sin x + 1.
The
function # has been given a high priority, since expressions like
#t+1 are so common that it would be a nuisance to have to
parenthesise these, and more so since
#(t+1) is meaningless anyway.
The reason for the high priority of the function ~ is to make ~0,
for example, for all practical purposes behave as a constant. The 'formatting' functions
<<, ><, and >> have the lowest priority since they
are practically always intended to operate on the whole preceding
expression.
Example zeroadic-formula: monadic-formula: dyadic-formula:
pi round(100*x) 2 round x
A formula whose function is defined by a how-to is evaluated in the following steps:
The evaluation of the formula is complete when the execution of this command-suite terminates because of the execution of a return-command; the value of the formula is the value returned.
Note that in contrast to command-how-to's where results may be passed back to the parameters, one may safely use template-operands, and even shared names, in a function-how-to for intermediate computations.
|
returns the text consisting of t and u joined. For example,
|
|
|
returns the text consisting of n copies of t joined together. For
example,
|
|
|
returns the initial part of t consisting of the first n characters.
For example,
|
|
|
returns the final part of t obtained by deleting the first n-1
characters (and so starting at the n'th character). For example,
|
|
|
returns the text t with all upper-case letters replaced by their
lower-case equivalents. For example,
|
|
|
returns the text t with all lower-case letters replaced by their
upper-case equivalents. For example,
|
|
|
returns the text t with spaces stripped off from the beginning and
end. For example,
|
|
|
splits the text t into the parts separated by spaces, and returns a
table whose keys are integers from 1 upwards, and whose items are
the parts. For instance,
|
|
returns a compound of 6 numbers representing the current date and time (year, month, day, hours, minutes, seconds), with year > 1900, month ∈ {1..12}, day ∈ {1..31}, hour ∈ {0..23}, minute ∈ {0..59}, and 0 ≤ seconds < 60. The accuracy of seconds is dependent on the operating system. For
example, |
|
requires a table as operand, and returns a list of all keys in the table. For example,
|
|
returns the number of
items in the train t (where duplicates in texts and lists are
counted). For example,
|
|
|
returns the number of items in t that are
equal in value to i (which must be of the
same type as the items of t). For
example,
|
|
|
returns the smallest item of t (for a text: first in the ASCII
order, see section Values in ABC . For example
The
value of t must not be empty. To get the
smallest (first) key of a table |
|
|
returns the smallest item in t exceeding the value of i (which must
be of the same type as the items of t). For example
There
must be an item in |
|
|
like
|
|
|
returns the n-th item of t. The value of n must be an integer in
the range {1..#t}. In fact, |
|
|
returns an item chosen at random from t. In evaluating the formula
|
|
returns x converted to a
'left-adjusted' text,
that is, with space characters added to the right to make the
length n. For example,
See write-commands, section WRITE, for details about converting values to texts. |
|
|
returns x converted to a 'centred' text, that is, with space
characters added to both the left and the right, to make the length
n. For example,
|
|
|
returns x converted to a 'right-adjusted' text, that is, with space
characters added to the left to make the length n. For example,
|
refined-expression:
The name of a refined-expression must occur as the name of one expression-refinement in the how-to in which it occurs.
Example refined-expression:
stack.pointer
A refined-expression is evaluated in the following steps:
The evaluation of the refined-expression is complete when the execution of this command-suite terminates because of the execution of a return-command; the value of the refined-expression is the value returned.
See also: expression-refinements (in Refinements).
An address is located to give a location, which may already exist, or be created to accommodate a value that is to be put in the location. A multiple-address refers to a multiple location , consisting of a combination of two or more single locations, called its components. A single location may hold arbitrarily complex values. Parts of text and table locations can be selected as locations of their own, in which values can be put without affecting the remainder of the text or table.
address:
basic-address:
Example multiple-addresses:
nn, t2 (x0, y0), (x1, y1), (x2, y2), (x3, y3)
naming:
single-naming:
( naming )Namings are a restricted form of addresses; that is, all namings can be used as addresses, but the converse is not true. For example,
FOR a[1] IN {1..3}: WRITE a
is wrong,
because a[1], although an
address, is not a
naming.
Example namings: single-namings:
a a (a) (a) (a, b, (c, d)) (a, b, (c, d)) a, b, (c, d)
A naming is located by locating it as if it were an address.
See also: PUT .
text-selection-address:
Example text-selection-addresses:
t|1 t@p t|q@p t@p+1 t@p|q-p+1
The address must hold a text T, and the value of the single-expression must be an integer N. If the sign used is |, then the text-selection-address indicates a location consisting of the first N characters of T, or, if N exceeds the length of T, consisting of the whole of T. N must be at least 0. A new text put in this location replaces these characters. For example, after
PUT "computer" IN tt PUT "ne" IN tt|4
tt will
contain the text "neuter".
If the sign used is @, then the text-selection-address indicates a location consisting of the characters of T starting with the N-th character, or, if N is less than 1, consisting of the whole of T. N must be at most one more than the length of T. A new text put in this location replaces these characters. For example, after
PUT "computer" IN tt PUT "ass" IN tt@5
tt will
contain the text "compass".
Note that the address itself may be a text-selection-address again. For example, after
PUT "computer" IN tt PUT "m" IN tt@4|1
tt will
contain the text "commuter".
Some special cases:
PUT "" IN t|1 removes the first character of the text in t;
the same as PUT t@2 IN t.
PUT "." IN t@#t+1 appends a period to the text in t, the same as
PUT t^"." IN t.
table-selection-address:
[ expression ]Example table-selection-address:
t[i, j]
The location of the address must hold a table. The value of the expression is a key K, to be used as selector. For each key in the table, there is a location for the corresponding item. If K is an existing key of the table, the location for the table-selection-address is that of the item corresponding to K. If a value I is then put in this location, the original item held in that location is superseded by I. If K is not an existing key and a value I is to be put in the table for this key, a new table entry consisting of K and I is inserted in the table. K must be of the same type as the other keys of the table, and I of the same type as the other table items.
Tests are performed and do not return a value, but succeed or fail.
Performing a test cannot alter the values of addresses that currently exist, nor can it create new addresses that survive the test, with the exception of the temporary survival of bound names as described under QUANTIFICATIONS (section Quantifications) and REFINED-TESTS (section Refined tests). If a test appears to alter a location, it effectively modifies a private, 'scratchpad' copy, and the change is invisible outside the test.
test:
tight-test:
( test )right-test:
The various kinds of tests that are distinguished here serve to define the syntax in such a way that no parentheses are needed when the meaning is sufficiently clear.
order-test:
(The
order-sign <> stands for 'not equals'.)
Example order-tests:
(i', j') > (i, j) "0" <= d <= "9" fa <= f(x) >= fb
The single-expressions of an order-test must all have the same type. They are evaluated one by one, from left to right, and each adjacent pair is compared. As soon as a comparison does not comply with the given order-sign, the whole order-test fails and no further single-expressions are evaluated. The order-test succeeds if all comparisons comply with the specified order-signs.
An approximate number x is compared with an
exact number e by applying the function exactly to x (see section
Functions on numbers) and comparing the result with e.
Two exact numbers are equal if their numerical values are identical. Similarly two approximate numbers are equal if their numerical values are identical.
Two trains are equal if they have the same length, and their corresponding items, if any, are equal. Similarly, two compounds are equal if their corresponding fields are equal.
An exact number is smaller than another exact number if the numerical value of the first is smaller than that of the second. Similarly for two approximate numbers.
A train is smaller than another train if the first differing item in the first train is smaller than the corresponding item in the second train or if the length of the first train is smaller than that of the second, and all its items, if any, are equal to the corresponding items of the second.
Similarly, one compound is smaller than another if the first differing field of the first is smaller than its corresponding field in the second.
For instance, the following all succeed:
"" < "a" < "ab" < "abc" < "abd" < "ac" < "b"
examination:
zeroadic-examination:
monadic-examination:
dyadic-examination:
zeroadic-predicate:
monadic-predicate:
dyadic-predicate:
An examination whose predicate is defined by a how-to is performed as follows:
The performing of the examination is complete when the execution of this command-suite terminates because of the execution of a report-, succeed- or fail-command; the examination succeeds or fails accordingly. Note that the operands of predicate- and function-how-to's are treated in exactly the same way.
refined-test:
Example refined-test:
special.case
A refined-test is performed in the following steps:
The performing of the refined-test is complete when the execution of this command-suite terminates because of the execution of a report-, succeed- or fail-command, and the refined-test succeeds or fails accordingly.
Any bound names set by a for-command or a quantification (see Quantifications) at that time will temporarily survive for those parts that are reachable only by virtue of the outcome of the test. This is so that you can turn any test into a refined-test with the same effect.
For example, in
IF divisible AND n > d**2: WRITE d
...
divisible:
REPORT SOME d IN {2..n-1} HAS n mod d = 0
the bound
name d is set to a divisor of n if the
refined-test succeeds, and since the part n > d**2 is only
reached after success, d may be used there. The same is true for
the write-command using d. However, the line after (indicated with
three dots) can be reached if the divisibility test fails, so there
d has ceased to exist and may not be used.
See also: test-refinements (in Refinements).
conjunction:
AND right-testAND conjunctionExample conjunctions:
a > 0 AND b > 0 i in keys t AND t[i] in keys u AND u[t[i]] <> "dummy"
The tests
of the conjunction, separated by AND, are performed one by one,
from left to right. As soon as one of these tests fails, the whole
conjunction fails and no further parts are performed. The
conjunction succeeds if all its tests succeed.
disjunction:
OR right-testOR disjunctionExample disjunctions:
a <= 0 OR b <= 0 n = 0 OR s[1] = s[n] OR t[1] = t[n]
The tests
of the disjunction, separated by OR, are performed one by one, from
left to right. As soon as one of these tests succeeds, the whole
disjunction succeeds and no further parts are performed. The
disjunction fails if all its tests fail.
negation:
NOT right-testExample negation:
NOT a subset b
A negation succeeds if its right-test fails, and fails if that test succeeds.
Quantifications are easy ways of finding out if a test is true for no items, or at least one, or every item of a train.
quantification:
HAS right-testExample quantifications:
SOME i IN samples HAS NOT low <= i <= high
EACH i, j IN keys t HAS t[i, j] = t[j, i]
NO d IN {2..n-1} HAS n mod d = 0
The names of the naming of a quantification are 'bound names', and so may not be used outside the quantification except as described below.
The meaning of quantifications will first be described for the case of SOME. The value of the expression must be a train. One by one, each item of that train is put in the location of the naming, and each time the right-test is then performed. The quantification succeeds as soon as the right-test succeeds once. It fails only if the train is exhausted without the right-test ever succeeding (thus also if the train is empty).
If the quantification succeeds, the bound names set at that moment will temporarily survive and may be used in those parts that are reachable only by virtue of the outcome of the test.
For example, in
IF (SOME d IN {2..n-1} HAS n mod d = 0) AND n > d**2:
WRITE d
the bound
name d is set to a divisor of n if the quantification succeeds, and
since the part n > d**2 is only reached after success, d may be
used there. The same is true for the write-command using d. So, if
n has the value 77, 7 will be written, since the test n mod d = 0
succeeds the first time when d is set to 7 (and 77 > 7**2).
However, the line after (indicated with three dots) can be reached
if the divisibility test fails, so there d has ceased to exist and
may not be used.
The
meaning of a quantification SOME id IN train HAS prop can also be
described as the meaning of the refined-test test.if.some, given a
test-refinement
test.if.some:
FOR id IN train:
IF prop: SUCCEED
FAIL
The
meaning of EACH id IN train HAS prop is the same as that of
NOT SOME id IN train HAS NOT prop.
In other words, an EACH
quantification succeeds only if its right-test succeeds each time,
or the train is empty.
The
meaning of NO id IN train HAS prop is the same as that of
NOT SOME id IN train HAS prop. In other words, a NO quantification succeeds
only if its right-test fails each time, or the train is empty.
The rules
for temporary survival follow from those for SOME. So an EACH or NO
quantification will only have set its bound names on failure. Thus,
in the following, the bound name d survives into the ELSE:
SELECT:
NO d IN {2..n-1} HAS n mod d = 0: WRITE "prime"
ELSE: WRITE "divisible by `d`"
See also: FOR .
The ABC Programmer's Handbook by Leo Geurts, Lambert Meertens, and Steven Pemberton
Copyright © 1990, 2002, Leo Geurts, Lambert Meertens, and Steven Pemberton. All rights reserved.