Issue
Article
Vol.28 No.2, April 1996
Article
Issue
Issue |
Article |
Vol.28 No.2, April 1996 |
Article |
Issue |
An aspect of usability that has often been downplayed in previous HCI modelling research involves time. Time dependencies and temporal constraints are an important aspect of action, and failure to meet them leads to an important class of human errors; many of the errors associated with safety critical systems have a significant temporal component. An attempt is made to show how properties and behaviours that are important from this temporal perspective may be modelled using concepts from our previous work [7] and using real-time CSP [2]; some of the issues and problems with such approaches are examined.
The main contribution of this paper is to investigate time in task performance by applying a particular modelling notation, and to discuss some general points about the requirements for such languages. In order to illustrate the concepts, an example scenario from the domain of air traffic control is investigated. The purpose of the example is to draw out some of the issues important in time-critical domains, rather than to be representative of all such systems. The example will highlight the significance of temporal deadlines and concurrent activities as important factors in task performance, and aims to show how designers may wish to understand the relative contributions of the tightness and number of deadlines and operator workload to interface usability.
An example scenario where there are numerous temporal constraints and where failure to meet the constraints may have a serious implications is described in [4], a simplified variant of which is used here as an exemplar. The scenario concerns an air traffic controller whose task is to schedule the arrival of aircraft at an airport, while maintaining an adequate separation distance between them. This example is representative of a large class of domains where real-world processes are controlled and hard timing constraints apply, and where the behaviour of the human operator has a significant impact on overall system safety. The starting point of the situation described in this paper is summarised in Figure 1 and how the scenario might develop over time is shown in the timeline diagrams of Figures 2 and 3.
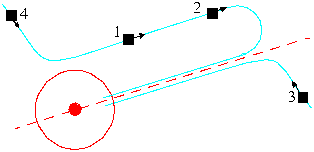
Figure 1: An Air Traffic Control Scenario
The situation in Figure 1 is as follows. Three aircraft, 1, 2 and 3, are on their final approach sector under the guidance of the controller in question, approaching an airport located inside the circle. A fourth, 4, is in the process of being handed off by another controller (it has appeared on the screen and is awaiting acceptance and confirmation). Aircraft 1 and 2 are on their "downwind leg" and are to be turned onto a heading towards the runway. Before 2 can be turned it must reduce speed. This means that 1 must reduce speed also to avoid loss of separation with 2. Aircraft 3 also must be turned towards the runway; if this does not happen, it will cross the path of other traffic and lose separation.
In common with the models of human-computer interaction proposed by Norman [6] and Card, Moran and Newell [1], it is assumed that interaction consists of three kinds of process. Properties of the world are perceived or recognised, a plan of action is formulated, and the physical actions are carried out.
An example trace of behaviour is shown in Figure 2 where the controller's actions of issuing commands to slow, turn and accept aircraft (events slow[i], turn[i], and accept[i] for aircraft i) are indicated along with the activities of perceiving system properties and planning the actual actions to be performed (perceive[i] and plan[i]). For example the "plan[2]" activity represents all the planning activity associated with aircraft 2, and results in the actions "slow[2]" and "turn[2]" (commands to the relevant pilot) being performed. The dashed lines indicate how much "leeway" or free time the controller has in order to complete the planning and decision making process. Also indicated is the time t[3] by which the turn of aircraft 3 must be completed.
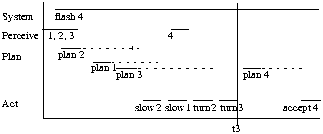
Figure 2: A Timeline
Suppose the controller decides to perform the actions in a different order, resulting in the timeline of Figure 3. The initial configuration and deadlines are the same, but activities are performed in a different order. The main point is that, by performing a less time-critical action first (accepting the hand-off of 4), less time is allowed for the subsequent planning and decision making.
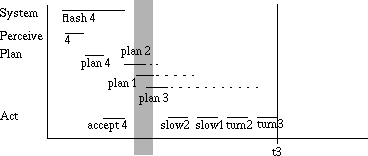
Figure 3: The effect of a bad ordering on leeway and time pressure
This is reflected in two ways: the lengths of the dashed "leeway" lines are reduced, and more than one planning activity is carried out at once (indicated by the shaded zone). Both of these facts add to the difficulty of the controller's task and increase the likelihood of the wrong actions being performed or actions not being performed in time.
Note that standard operating procedures for controllers tend to reduce the likelihood of this kind of bad planning. It is generally the case that as aircraft approach the runway, their behaviour becomes more time-critical. Controllers, therefore, adopt a "scan pattern" beginning at the runway (or outer marker), moving out along the localiser (the dashed line in Figure 1), and back along the downwind leg. Aircraft 4 would therefore be the last to be seen and dealt with.
The main aim of this note is to look at how existing techniques may be used to model scenarios such as this. The reason for doing this is to make predictions about how reliable the human-machine system is likely to be in achieving its goals and maintaining safe operating conditions (which in this case means not violating separation rules). Understanding how reliable an interaction sequence is depends on the following factors. What happens if one of the actions is not performed? What happens if actions are done too early or too late? How hard must a human work at each stage in the task (and therefore, where are the likely points of error and most fruitful opportunities for re-design)? What happens if actions are done in the wrong order? Are goals still achieved? Is there an impact on time pressure?
In order to answer these questions, a number of important features of interactions may be discerned. Of particular importance are situations where there are deadlines by which the user must complete some action, and concurrency, where the user may have to perform several perceptual, cognitive or physical actions at once.
Previous work [7] has looked at how a representation of user tasks and system behaviour maybe used to analyse a system's tolerance to erroneous human action. The approach is based on Hierarchical Task Analysis and uses the CSP process algebra notation to represent both user procedures (or plans) and system interface constraints. The method develops additional system requirements to make the system more "error tolerant", by identifying possible errors as syntactic "mutations" of a correct prescribed procedure. A model of the system's response to user input is used to identify which errors have the most significant impact, and therefore deserve the most attention from the designer.
In this section, we look at how the modelling framework of [7] might be applied in the scenario above. The controller's task here consists of four sub-tasks, one for each aircraft, which can be represented as a CSP processes Task1 -Task4.
Task[1] = perceive[1] -> plan[1] -> slow[1] -> turn[1] -> Skip
Task[2] = perceive[2] -> plan[2] -> slow[2] -> turn[2] -> Skip
Task[3] = perceive[3] -> plan[3] -> turn[3] -> Skip
Task[4] = perceive[4] -> plan[4] -> accept[4] -> Skip
The overall task of the user can be modelled by the parallel combination of these processes. Sequencing constraints imposed on the interaction by the domain can also be represented as a process. Errors may be considered to be "mutations" of these processes. So, for example, the error of reversing the slow and turn commands is represented by replacing "slow[1] -> turn[1]" by "turn[1] -> slow[1]" in the definition of Task1 above. The effect the traces of this revised process have on the system can be studied either using expert judgement and domain knowledge (as in [7]) or using a formal model of system behaviour (as in [3]). If errors are judged to be significant (either because they are likely to occur, or because their effects are serious), then the designer may opt to build in extra interface features to make the error less likely, mitigate against its effects or allow the user to diagnose and recover from the problem.
While the existing notation developed by [7] is capable of treating several classes of user-related properties, hard real-time issues are not representable. In the context of the air traffic control scenario, neither the requirement that the action turn[3] be performed before time t[3], nor the fact that at certain times the human may be doing several things at once are representable. In general, issues such as how much leeway or free time a user has for performing actions, how this is affected by "scheduling" decisions, and the extent to which a human may or must perform activities in parallel, cannot be discussed meaningfully.
An obvious way to try and address these problems is to extend the models in a fairly conservative way, using an "off the shelf" extension of CSP designed to address timing issues. The variant chosen is the real-time CSP of Davies and Schneider [2]. The question is, is such a extension adequate?
The real-time CSP notation adds a number of operators to the CSP language. For our purposes, the most significant are delays and timeouts. The process Wait t simply waits for t time units, performing no actions. The process P 
{t} Q is initially prepared to behave like process P, but if no events occur for t time units, then it times out and behaves like process Q.
Using the new notation, two types of properties can be represented: temporal aspects of the behaviour of the system or the world, and temporal properties of the human operator.
Two important properties of the behaviour of aircraft in this scenario which have a bearing on our discussion are as follows.
1 and 2 will lose separation if 2 isn't turned before t[2].
3 will lose separation with the other runway if it's not turned before t[3].
These environmental properties can be represented as a collection of parallel processes. Loss of separation and other hazardous situations won't be represented explicitly, instead, a violation event is generated to indicate a hazardous situation in the environment.
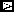{t[2]} violation -> Skip)||
{t[3]} violation -> Skip)||...
The kinds of temporal properties we might wish to record about the controller's behaviour reflect temporal delays and the length of time it takes to perform physical and cognitive actions. Such information may be collected as a result of experiments or be predicted by models such as GOMS or the CPM-GOMS variant [1, 5]. This may not appear to be easily representable in a CSP-based model, since events are assumed to be instantaneous, and represent points in time rather than ongoing activities. The best that real-time CSP is able to offer is to add new events to the model to mark the end of an action, and build in Wait events to specify the minimum time an action may take.
For example, to specify the property that planning the activities associated with aircraft 1 takes t[p] time units, a new event endplan1 is required and the following process added in parallel to the task description.
plan[1] -> Wait t[p]; endplan[1] -> slow[1] -> SkipWhile this may seem an inelegant solution, the semantics and proof theory of the real-time CSP notation can then be used to state and prove properties such as "is it possible to complete the turn of aircraft 3 by time t[3]?" or "is it possible to meet all the deadlines without having to do more than one thing at once?". Particular strategies adopted by the controller for scheduling the work may also be expressed as additional parallel CSP processes. For instance the strategy of considering the aircraft in the order 4, 2, 1, 3, as in Figure 3, may be represented by adding the following parallel process.
accept[4] -> slow[1] -> turn[2] -> turn[3] -> SkipThe same questions "is it possible to meet the deadlines?" and "must the user perform parallel activities in order to meet the deadlines?" may now be asked of the revised description. This kind of mechanism may be used to compare different approaches to the work (and different scan patterns), in terms of both their effectiveness and a crude measure of workload.
In general, a situation will consist of a number of tasks, each containing a perceive-plan-act cycle, and each with a temporal deadline by which the actions must be completed. In addition, a model allows predictions to be made about the effects of erroneous action sequences and failures to meet deadlines. Some general properties about deadlines etc., we may wish to know about are:
To some extent, at least, the kind of formalisation described above may be used to help answer questions such as these. If certain scenarios can be identified as being either problematic or advantageous, then design steps can be taken to discourage or promote them.
The aim of this paper has been to show how previous work is incapable of modelling adequately some of the "hard real-time" phenomena associated with the usability of safety-critical systems. The two important features of such systems are that user's goals are to effect some change to the world by a particular deadline, and that a major component of the workload of the user is the number of concurrent activities going on at any time. Modelling notations and frameworks should allow us to assess and predict these factors at an early stage in the design process (before the system exists in a form that supports experimentation).
A real-time extension to the CSP process algebra notation has been investigated as a candidate, in part because its use represents a fairly conservative extension of our previous work [7, 3]. A disadvantage of the use of this notation, though, is that the way in which non-instantaneous activities are handled is somewhat complex, and involves the use of a pair CSP events to represent the beginning and end of each such activity. This means that any reasoning about of the time dependent properties mentioned above will be highly complex.
Future work will investigate how other notational frameworks can contribute to modelling time in tasks with a view to making predictions about how temporal aspects of usability. Of particular interest will be real-time temporal logics and process algebraic formalisms which allow the representation of the duration and concurrency of user actions in a convenient and concise way.
Issue |
Article |
Vol.28 No.2, April 1996 |
Article |
Issue |