Issue
Article
Vol.28 No.2, April 1996
Article
Issue
Issue |
Article |
Vol.28 No.2, April 1996 |
Article |
Issue |
This paper addresses the problem of the representation of time in interactive software models. We aim at providing solutions allowing the software designers to efficiently use time modelling during the design process, and to check that the software being built actually corresponds to the temporal requirements. The modelling approach makes a precise distinction between qualitative and quantitative time modelling. The qualitative aspects are presented according to basic constructs of Petri nets while quantitative aspects are introduced according to several extensions to the basic constructs of Petri nets. Each of those constructs is presented on a simple example.
Keywords: Formal models, Petri nets, time modelling, temporal relationships
The need for formal techniques in order to design and specify interactive systems is widely acknowledged. Indeed, due to their intrinsic nature, interactive systems are very hard to specify and to test and thus the use of formal methods provides designers with mathematical tools that allow them to perform proofs on their specification before implementation. Besides, several techniques [Dix 91, Johnson 92, Duke 93, Paterno 92, Palanque 94] based on various formalisms and frameworks are available for designers. However, [Dix 91, Duke 93] are more concerned with abstractions in interactive systems while the other ones [Johnson 92, Paterno 92, Palanque 94] aim at providing specifications precise enough to allow executing them. These techniques have proven their capability to describe WIMP (Window, Icon, Menu, Pointing) interfaces but seem to need extensions in order to cope with highly interactive systems. Indeed, those systems require features that are not mandatory in more conventional interactive systems.
By highly interactive systems we mean interactive systems featuring non conventional input/output devices such as multimodal, multi-media, animated or virtual reality systems.
The modelling of time is a requirement for any formalism attempting to describe such systems. Multimodal systems [Nigay 95] rely on time related information while constructing high level input statements expressed using a combination of concurrent multimodal inputs. The definition of temporal windows is necessary in order to gather relevant pieces of input from the input flow. In animated interfaces the evolution of the systems is both driven by user events and by clock and timer events.
This paper aims at showing how several aspects of time modelling may be undertaken within the Petri net formalism. This work is based on previous work presented by the authors on the ICO formalism [Palanque 94] which is devoted to the design, specification and verification of WIMP interactive systems.
The various approaches in time modelling in Petri nets are successively presented. Then an example is proposed to illustrate the modelling constructs.
This sections aims at describing two main approaches in time modelling: Qualitative and quantitative. These two approaches are illustrated using Petri nets [Peterson 81]. Another kind of distinction can be done depending if you have to describe linear time or branching time. In linear time you only describe chaining of actions along the time axial while in branching time several different futures can occur and you described how and when the branching is made among the set of possible futures.
When modelling with Petri nets, a system is described in terms of state variables (called places, depicted as ellipses) and by state-changing operators (called transitions, depicted as rectangles), connected by arcs. The state of the system is given by the marking of the net, which is a distribution of tokens in the net's places.
State changes result from the firing of transitions, yielding a new distribution of tokens. Transition firing involves two steps: (1) tokens are removed from input places, and (2) new tokens are deposited in the output places. A transition is enabled to fire when all of its input places contain tokens.
A macrotransition is a net which begins by a transition Start and finishes by a transition End, and that besides verifies several structural properties that ensure it behaves like a normal transition [Valette 79] (informally, at each firing of the Start transition corresponds one and only one firing of the End transition).
Most formalisms take a qualitative approach towards time modelling: They are concerned mostly in describing a partial ordering of state changes in the system. Those approaches allow to state temporal relationships between actions, such as before, after and meanwhile. Those relationships are basic constructs that may be combined into more elaborated ones, such as interleaving and order independence in UAN [Hartson 92, Hix 93].
Petri nets have originally been designed in order to model such constructs in a concise and accurate way.
Figure 1 describes a total ordering between actions A and B, stating that actions B may start only after A has completed, thus showing how After and Before constructs are modelled using Petri nets.
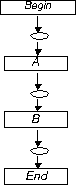
Figure 1: Sequence
The construct in Figure 2 describes the order independence in the performance of action A and B. This may be understood in one of two ways:
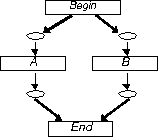
Figure 2: Meanwhile
If A and B are atomic transitions, the constructs states that action A may complete before action B starts, or B may complete before A, and that the precise ordering is left undetermined in the specification (this undeterminism may be relieved in either way when executing an actual implementation).
If A and B are macro-transitions modelling more complex subsystems, this specification describes that A and B may be performed concurrently (thus describing the meanwhile construct). Hierarchical refinement allows constructing such complex structures out of basic constructs as illustrated in Figure 3.
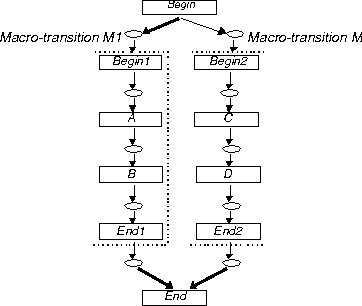
Figure 3: Combining Meanwhile and Sequence
Qualitative time modelling is concerned about precedence, sequences and interleaving between actions. Conversely, quantitative time modelling is concerned about delays, dates and duration.
A lot of work in Petri nets theory has been devoted to the smooth integration of quantitative time modelling. The main objective of this integration is to do performance evaluation on the models, in order to obtain quantitative results.
Timed places. Time may be associated with the places of a Petri net. In this case, a place models an operation that takes some time to complete, while a transition models an event occurring in the system so that operations may start.
A duration d may be associated to each place in the model. This duration indicates that a token entering the place at date t will not be available until date t+d for the following transition occurrences [Sifakis 77].
Timed transitions. Time may be associated with the transitions of a Petri net. In this case, a place models a state variable of the system, while a transition models an action that consumes tokens, and takes some time to complete before setting the tokens into its output places.
A duration d may be associated to each transition in the model. This duration indicates that if the transition occurrences starts at date t, tokens will be set in the output places at date t+d [Ramchandani 74].
In order to describe probabilistic systems (such as occurrences of failures in hardware), duration may be expressed as laws of probability [Ajmone 85, Natkin 80]
Timed arcs. Two different approaches have been proposed with temporal constructs on arcs.
Arc-timed Petri nets [Alla 87] permit to model the fact that the duration of a transition may vary according to the output places where token will be deposited.
Temporal arcs in Petri nets [Bastide 89] permit to model that tokens in places are removed by transitions according the duration of their stay in the place. This kind of construct is very useful while coping with situations where an alarm has to take place when a normal sequence cannot be performed within a predefined delay. An example of such a "watch-dog" modelling using temporal arcs is shown on Figure 4. This model describes the handling of eggs that are stored in one's refrigerator: After the eggs are purchased, they must be eaten before 15 days have elapsed. In order to eat an egg, one needs a fork, that has to be cleaned after use. If an egg is not eaten after 15 days, it is thrown in the garbage. The timing notation is added to the arcs between place Eggs and transitions Garbage and Eat. Without this timing notations, those transitions would be in structural conflict (corresponding to indeterminism in the choice between Garbage and Eat).
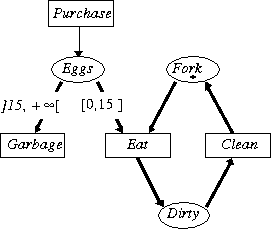
Figure 4: Modelling a watchdog using temporal arcs
Time on arcs is a very efficient way of describing branching time. Another one widely used within the Petri net community is the Stochastic Petri net approach where transition firing times are mutually independent exponentially distributed random variables [Natkin 80, Molloy 82]. For space reason we will not present this kind of time modelling, even though we think they can be of great help for computing performance evaluation on the interaction between the human and the computer.
To illustrate the use of such notations, let us model a toy example.
The system consists in a light bulb controlled by a timer, and a stop-watch. The timer is triggered by a button, and its period is 30 seconds. If the button is depressed while the light is on, the timer is reset and starts over counting down for 30 seconds. This system has been chosen because it is widely used in continental Europe and more precisely in France. This kind of switch is used for outdoors lights or for staircase ones. Even though this device is not related to computers one can notice that screen saver or several other time related systems present the same particularities.
The model in Figure 6 is a Petri nets featuring temporal arcs in order to describe the time-driven behaviour of the system.
Figure 5:A simple system
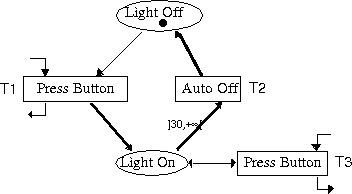
Figure 6: Model of the switch system
At the initial state the light is off (represented in the model by a token in the place Light Off. From this state, the only action available to the user is to press the button (as only the transition T1 can be fired). If the user press the button (transition T1 is fired) the token in place Light Off is removed and set into place Light On stating that the new system state is Light On.
From that state two transitions (T2 and T3) may occur. T3 may occur at any time (the user can press the button when he/she wants) while T2 may only occur after the token deposit in place Light On has remained there for 30s. It is important to notice that transitions T1 and T3 correspond to user actions (this is represented in the model by incoming broken arrows) while T2 correspond to spontaneous activity of the system.
This simple example has only shown how to model qualitative time modelling using timed Petri nets. Due to the mathematical foundations of Petri nets and the work previously done in Petri nets theory, it is possible to make static and dynamic analysis on timed Petri nets. Several theoretical results have been presented in the International workshop on Timed Petri Nets held in Turin in July 1985, but none of them have been applied to the verification of interactive systems.
Due to space reasons analysis on timed Petri nets is not presented here, but the kind of analysis that can be done is for instance, performance evaluation (how long does it take to at least to switch off the light), number of actions (how many times the user has to press the button in order to have the light on for 5 minutes)., etc.
This position paper has presented how Petri nets can be used for time modelling in the design of interactive systems. We have successively described the different approaches and what are their different ways to include time in models. Then the model of a simple system has been described using timed Petri nets. At present time, part of the work we are doing is to use the same formalism in order to describe user tasks [Palanque 95a] where time modelling is very important in order to make evaluation on the user workload (sequences of action that have to be performed under temporal constraints are very stressful for users).
Issue |
Article |
Vol.28 No.2, April 1996 |
Article |
Issue |