Een citaat (uit een beschrijving van de geschiedenis van de PDP8):
Once PS/8 became useable, assembly language software development on the
PDP-8 became common. Prior to the development of PAL8, the symbol
table in PAL III was too limited to assemble anything other than small and
medium size programs. The MACRO-8 symbol table was even smaller. PAL8,
however, was derived from the MACRO-8 paper tape assembler (maybe a
descendent of MACRO-8.) The macro features were removed, and the symbol
table was moved to extended memory, vastly expanding its size. But PAL8
was still very slow until someone, I think Richie Lary, implemented a
binary search on the PAL8 symbol table. That remains, in my mind, a
defining moment, where the PDP-8 became a useful computer rather than an
interesting toy. Subsequently, OS/8 and all associated system software
and DEC PDP-8 programming languages could be developed entirely on the
PDP-8 using OS/8 and the PAL8 assembler.
Hetzelfde probleem (in dit geval: het opzoeken van een naam in een alfabetisch geordende lijst) kan op meer dan een manier opgelost worden. Sommige manieren zijn veel sneller dan andere, en dat speelt een rol in de bruikbaarheid van het resulterende programma.
Behalve snelheid zijn ook geheugengebruik en (bij berekeningen met reele getallen) nauwkeurigheid en stabiliteit belangrijke eigenschappen van algoritmen.
Snelheid en geheugengebruik van algoritmen hangen ook erg af van de manier waarop de gegevens opgeslagen zijn.
Bijvoorbeeld: Als ik een naam in een niet-gesorteerde lijst moet zoeken dan zit er niets anders op dan de lijst af te lopen tot ik de naam gevonden heb. Bij een lijst ter lengte N kost dit gemiddeld N/2 stappen. Heel onhandig, als dit het telefoonboek van Amsterdam was (met N=300000 is N/2=150000). Maar is de lijst gesorteerd, dan kan ik naar het middelste element kijken, vaststellen of ik daarvoor of daarna moet zijn, dan de overgebleven helft en tweeen delen, enz. Deze `binary search' kost log(N) stappen (logaritme met grondtal 2), dus niet meer dan 19 stappen op het telefoonboek van Amsterdam. Dit bijna tienduizend keer zo snelle algoritme wordt mogelijk gemaakt door de handige manier van bewaren van de gegevens: als gesorteerde lijst.
Vaak is er ook een `time-memory trade-off': je kunt kiezen tussen verschillende manieren om de gegevens te bewaren, en manieren die snellere algoritmen toelaten kosten meer geheugen.
Als extreem voorbeeld: stel voor het gemak dat de telefoonbezitters in Amsterdam allen verschillende achternamen hebben, en zelfs dat er al een verschil is in de eerste acht letters van de achternaam. Beschouw de letters A-Z als cijfers van het 26-tallig stelsel, zodat de eerste acht letters van de achternaam (of de hele naam, als deze korter is) als een getal gelezen kan worden. Berg het telefoonnummer op dit adres in het geheugen op. Mijn telefoonnummer zou op adres 517663345 staan. Nu kost het opzoeken maar 1 stap: je kunt gelijk op de goede plaats kijken, geen zoeken of vergelijken nodig, alleen een kleine omrekening uit het 26-tallig stelsel. Aan de andere kant wordt wel tamelijk veel geheugen gebruikt: 26^8=208827064576 dus met 10-cijferige nummers is dit 2088 GB oftewel 2 TB.
(Er zijn ook heel andere versies van een `time-memory trade-off' - hoop hier op terug te komen.)
Als 1 computer N getallen moet sorteren, dan kost dat N log(N) stappen. Bij slechte algoritmen N^2 stappen. Bij vreselijk slechte algoritmen misschien N! stappen of meer.
Hoe sorteer ik 100 CDs op componist in een CD rekje? Een vreselijk slecht algoritme zou zijn: zet de CDs op het rekje zonder op de componist te letten. Staan ze nu toevallig op volgorde dan zijn we klaar. Gooi ze er anders weer uit, schuffel ze, en begin opnieuw. Na N! pogingen is de kans dat het nog steeds fout is ongeveer 36% (namelijk 1/e).
Aanzienlijk beter zou zijn om eerst de stapel te doorzoeken naar de CD die het eerst moet komen, dan de resterende stapel naar de kandidaat voor de tweede plaats, enz. Dit kost N+(N-1)+...+1 = N(N+1)/2 stappen (met N=100: 5050).
Vergelijkbare complexiteit heeft het algoritme: Zet de eerste CD op de eerste plaats. Zet de tweede CD er achter als dat zo hoort, of verplaats de eerste CD een vakje en zet de tweede er voor. Enz. Als we vreselijk veel pech hebben kost dit 1+2+...+(N-1) = N(N-1)/2 verplaatsingen, maar gemiddeld hoort elke nieuwe CD ergens in het midden van het rijtje al geplaatste CDs, en kost deze methode iets als ruwweg N^2/4 stappen.
Dit soort voorbeelden laat zien dat sorteren van N dingen, wanneer dit op een naieve manier geimplementeerd wordt, ongeveer cN^2 stappen kost, voor een zekere constante c die niet groot is. Als N heel klein is, bijvoorbeeld kleiner dan 10, dan is de eenvoud van het programma meestal belangrijker dan de kleine snelheidswinst die eventueel geboekt zou kunnen worden. Maar als N groot is, bijvoorbeeld groter dan 1000, dan is het absoluut noodzakelijk om een algoritme te gebruiken dat niet kwadratisch is.
Een voorbeeld van een veel efficiënter versie is `sort-merge'. De definitie is recursief: Om N getallen te sorteren hoef ik niets te doen als N <= 1. Als N >= 2, verdeel de stapel dan in twee gelijke helften, sorteer beide helften, en voeg de twee gesorteerde stapeltjes dan weer samen tot één stapel door telkens naar de bovenste elementen van beide stapeltjes te kijken, en degene te pakken die het eerst komt.
Hoeveel tijd kost dit? De `merge' fase, het samenvoegen van twee stapels elk ter grootte N/2 kost N stappen. Als s(N) de tijd is die nodig is om N dingen te sorteren op deze manier, vinden we s(N) = 2s(N/2) + N. Als t(N)=s(N)/N dan staat hier t(N) = t(N/2)+1. Dus t(N) = log(N), waarbij log de 2-logaritme is, en s(N) = Nlog(N). Als N=1000 dan is N log(N) = 10^4 en N^2 = 10^6, dus sort-merge is hier honderd keer zo snel als kwadratisch sorteren. Als N=100 dan is N log N bijvoorbeeld 700 en N^2/4 = 2500, en we winnen nog steeds een factor vier. Als N=10 dan is N log N iets als 33 en N^2/4 = 25, en beide algoritmen hebben ongeveer dezelfde complexiteit.
Als N heel klein is (bijvoorbeeld 4 of 5 of 6) en het gebeurt miljoenen malen dat een groepje van N gesorteerd moet worden, dan is het zinvol hier aparte code voor te schrijven. Bijvoorbeeld: om a,b,c,d (vier verschillende getallen) te sorteren, vergelijk a met b en zet ze op volgorde, zeg a < b; vergelijk daarna c met b; is c groter dan is de volgorde a b c; is c kleiner, vergelijk c dan met a. Nu is de volgorde van a, b, c bekend na gemiddeld 8/3 vergelijkingen. Zeg a < b < c. Vergelijk nu d met b; als d > b, vergelijk dan d met c, anders met a. Nu is de volgorde van a, b, c, d bekend na gemiddeld 14/3 = 4.67 vergelijkingen.
Opgave Laat zien dat vijf getallen met 7 vergelijkingen gesorteerd kunnen worden.
Zulke speciale code kan op de bodem van de recursie van sort-merge gebruikt worden, maar asymptotisch maakt dat niets uit. (Bijvoorbeeld: N=128, Nlog(N)=896; met bovenstaand algoritme 789.)
Het optellen van twee n bij n matrices kost n^2 stappen. Het op de voor de hand liggende manier vermenigvuldigen van twee n bij n matrices kost orde n^3 stappen: voor elk van de n^2 elementen van het antwoord gebruiken we n vermenigvuldigingen en n-1 optellingen. Het kwam als een verrassing toen Strassen vond dat dit veel sneller kan. Zijn algoritme gebruikt O(n^2.81) stappen. Winograd en Coppersmith verbeterden deze grens tot O(n^2.38). Strassen's algoritme laat eerst zien hoe twee 2x2 matrices met 7 vermenigvuldigingen (in plaats van 8) vermenigvuldigd kunnen worden. Recursief gebruik van deze methode (splits een 2mx2m matrix op in vier mxm blokmatrices) levert dan een O(n^e) algoritme, waarbij e = log(7)/log(2) = 2.807. Het vermenigvuldigen van twee 2x2 matrices komt neer op het berekenen van
/ a b \ / e f \ / p q \ / ae+bg af+bh \ \ c d / \ g h / = \ r s / = \ ce+dg cf+dh /en dat kan ook als
p = x1+x2-x3+x4 q = x3+x5 r = x2+x6 s = x1+x5-x6+x7met
x1 = (a+d)(e+h) x2 = d(g-e) x3 = (a+b)h x4 = (b-d)(g+h) x5 = a(f-h) x6 = (c+d)e x7 = (c-a)(e+f)worden geschreven. Kortom, in plaats van 8 vermenigvuldigingen en 4 optellingen nu 7 vermenigvuldigingen en 18 optellingen en aftrekkingen. Als het vermenigvuldigen van matrices van orde 2^k een aantal van N(k) elementaire operaties kost, dan vinden we N(k) = 7N(k-1) + 18*4^(k-1), en met N(1) = 12 wordt dit N(k) = (36/7) * 7^k - 6 * 4^k. Kortom, bij matrices van orde 128 gebruiken we 4137060 operaties in plaats van 4177920. (In het echt duurt het wat langer voordat deze methode voordeliger wordt, omdat de administratie van de recursieve vermenigvuldiging ook wat ingewikkelder is.)
Het vermenigvuldigen van twee getallen of van twee veeltermen op de voor de hand liggende manier kost een tijd die kwadratisch is in de grootte van de getallen. Elk cijfer, of elke term, van de een wordt vermenigvuldigd met elk cijfer of elke term van de ander. Zo kost het vermenigvuldigen van twee getallen van 100 cijfers op de lagere school manier 10000 stappen. Kan dat ook sneller?
Net als bij sorteren is ook hier het antwoord ja, en deze N^2 stappen kunnen tot c N log(N) gereduceerd worden, alleen is c hier helaas niet zo klein, zodat deze methode pas interessant wordt bij heel grote getallen.
Het idee is om de Chinese Reststelling te gebruiken.
Het idee is dat we een getal kunnen voorstellen door de resten te geven bij deling door 2, 3, 5, 7, ..., en het vermenigvuldigen van die resten is makkelijk.
Sun Tzu schreef omstreeks het jaar 100 in het book Suan-Ching:
Als we ze met drie tegelijk tellen is de rest 2, Als we ze met vijf tegelijk tellen is de rest 3, Als we ze met zeven tegelijk tellen is de rest 2. Hoeveel dingen zijn er? Het antwoord, 23.
Hoe je dit antwoord vindt werd (veertienhonderd jaar later) verklaard door Hsin-Tai Wei in Suan Fa Tung Ching:
Drie mannen wandelden samen, zo gering hun kans zeventig te worden, De vijf pruimebomen gaven eenentwintig bloesems, Zeven zonen kwamen blij bijeen op de middelste dag van de maand. Deel de som door 105, het antwoord wordt onthuld.
Wat is de wiskunde hierachter? Als twee getallen x en y dezelfde rest hebben bij deling door m dan is y-x deelbaar door m. Als m1, m2, m3, ... onderling ondeelbaar zijn (paarsgewijs geen factor groter dan 1 gemeen hebben) en y-x is deelbaar door m1 en door m2 en door m3, ... dan is y-x deelbaar door het product m1*m2*m3*... Bijvoorbeeld, als x en y dezelfde rest hebben bij deling door 3, 5 en 7 dan is hun verschil deelbaar door 105. Als je weet dat het om getallen onder de honderd gaat, dan is het dus voldoende om deze drie resten te geven. En als het om getallen onder de 1000 gaat is het voldoende om de resten bij deling door 3, 5, 7, 11 te geven. En als het om getallen van niet meer dan 100 cijfers gaat, dan is het voldoende om de resten bij deling door 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251 te weten (zoals Mathematica leert: dit was de uitvoer van Table[Prime[i],{i,1,54}], en N[Product[Prime[i],{i,1,54}]/10^100] levert 6.42663, zodat het product van deze 54 priemgetallen groter dan 10^100 is). Hmm - maar dit betekent dat als we de 54 resten van x en y modulo deze 54 priemgetallen kennen, we de 54 resten van x*y modulo deze 54 priemgetallen met 54 vermenigvuldigingen (en delingen met rest) vinden, aanzienlijk minder werk dan de 10000 vermenigvuldigingen die eerst nodig waren. (En de benodigde vermenigvuldigingen en delingen met rest gaan over getallen onder de 251. Als het om snelheid gaat kun je de antwoorden in een tabelletje opslaan, zodat een vermenigvuldiging plus deling met rest 1 stap kost.)
Even uitproberen met de moduli van Sun Tzu: 3, 5 en 7. Nu is 8: (2,3,1) en 8*8 = (1,4,1). Dat was makkelijk. Maar welk getal is dit nu eigenlijk? De spreuk van Hsin-Tai Wei zegt: dit is de rest van 70*1+21*4+15*1 bij deling door 105, dus 70+84+15 (mod 105) = 64. Dit omrekenen is nog het meest bewerkelijke gedeelte van de vermenigvuldiging, maar kan ook in tijd O(N log(N)) gedaan worden.
Dus: vermenigvuldigen van heel grote getallen gaat veel sneller dan je zou denken. Dat betekent dat ook veeltermen snel vermenigvuldigd kunnen worden: om (X^5-7X^3+12X-1)(X^6-X^2+4) uit te rekenen kunnen we voor X bijvoorbeeld 1000 nemen, en het product 999 993 000 011 999 * 999 999 999 999 000 004 = 999 993 000 010 999 010 999 960 001 047 996 uitrekenen en aflezen dat het antwoord X^11-7X^9+11X^7-X^6+11X^5-40X^3+X^2+48X-4 is. Kortom: ook veeltermen van heel hoge graad met kleine coefficiënten kunnen snel vermenigvuldigd worden.
Voor precieze details, zie elders. De bedoeling van de sectie hier is tweeledig: (1) Laten zien dat er goede en slechte manieren zijn om iets uit te rekenen, en dat de voor de hand liggende methoden niet altijd de beste zijn. En (2) laten zien dat de efficiëntie van een methode sterk kan afhangen van de gekozen manier om de gegevens te representeren.
Hash, x. There is no definition for this word-nobody knows what hash is. [Ambrose Bierce, The Devil's Dictionary]
Het wat onrealistische voorbeeld hierboven met een 2 TB tabel met telefoonnummers, was een voorbeeld van een techniek die buitengewoon veel gebruikt wordt, namelijk het gebruik van hash codes. Een hash code is een gehaktmolen: je stopt er iets in, zeg x, en er komt iets uit, zeg hash(x). Wat je precies doet maakt helemaal niets uit, als het maar welgedefinieerd is (zodat als je hash(x) tweemaal uitrekent je tweemaal hetzelfde vindt; opgooien van een dobbelsteen is dus niet toegestaan). Een hash code werkt goed als de kans klein is dat hash(x)=hash(y) voor verschillende x en y.
Vaak berekent een hash functie een of ander groot getal H(x), en volgt als laatste stap een deling met rest: hash(x) = H(x) % M (waarbij % staat voor de rest bij deling, zoals bij C en Java gebruik is). Nu kan hash(x) als adres voor x gebruikt worden als een lijst ter lengte M beschikbaar is.
Het voordeel van een hash functie is dat er niet meer gezocht hoeft te worden: één kleine berekening en je weet waar je zijn moet.
Een `botsing' (collision) ontstaat als hash(x)=hash(y) voor verschillende x en y. Nu kan de beschrijving van x in de lijst voorzien worden van de aantekening `er volgt nog meer' en y bijvoorbeeld op adres hash(x)+1 worden opgeborgen. Als deze hash-slierten langer worden, gaat snel het voordeel van een hash functie verloren.
Kortom, òf men construeert een `perfect' hash - namelijk als het domein van de functie hash() bij voorbaat bekend is en de hash functie zo uitgevogeld kan worden dat geen botsingen optreden en de M verschillende waarden van x op de M getallen 0, 1, ..., M-1 worden afgebeeld, òf men kiest M zo groot dat de verwachte lengte van de hash-sliert klein is (d.w.z. dat slechts een kleine fractie van de lijst gevuld is).
Opgave Construeer een zo eenvoudig mogelijke perfecte hash functie voor de 7 strings "ma", "di", "wo", "do", "vr", "za", "zo", gegeven in ASCII code ('a'=97, ..., 'z'=122).
Als je op een computer alleen met gehele getallen rekent zijn de problemen tamelijk overzichtelijk. Eigenlijk moet je alleen oppassen voor overflow: berekeningen waarbij een tussenresultaat optreedt dat niet in de gebruikte getalrepresentatie is voor te stellen - bijvoorbeeld groter is dan een machinewoord. Meestal kun je zulke tussenresultaten vermijden, of anders meervoudige lengte aritmetiek gebruiken.
Bij het rekenen met drijvende komma (floating point) getallen kunnen echter de vreselijkste dingen gebeuren zonder dat je er erg in hebt.
Als ik een polynoom p(x) heb, en a is een wortel (nulpunt), dan is (x-a) een factor van p(x), en is dus p(x) = q(x)*(x-a) met q(x) een polynoom van graad 1 lager dan p(x). Zo voortgaande kun je telkens een wortel vinden, die wegdelen, en ophouden als het quotient constant is (of geen nulpunten meer heeft). In de numerieke wiskunde is dit een van de stomste dingen die je doen kunt.
Een Mathematica voorbeeld
Mathematica 3.0 for Linux
In[1]:= p[x_] := (x^2-2)^15
In[2]:= q0[x_] = Expand[p[x]]
2 4 6 8
Out[2]= -32768 + 245760 x - 860160 x + 1863680 x - 2795520 x +
10 12 14 16 18
> 3075072 x - 2562560 x + 1647360 x - 823680 x + 320320 x -
20 22 24 26 28 30
> 96096 x + 21840 x - 3640 x + 420 x - 30 x + x
In[3]:= Roots[q0[x]==0, x]
Out[3]= x == Sqrt[2] || x == Sqrt[2] || x == Sqrt[2] || x == Sqrt[2] ||
> x == Sqrt[2] || x == Sqrt[2] || x == Sqrt[2] || x == Sqrt[2] ||
> x == Sqrt[2] || x == Sqrt[2] || x == Sqrt[2] || x == Sqrt[2] ||
> x == Sqrt[2] || x == Sqrt[2] || x == Sqrt[2] || x == -Sqrt[2] ||
> x == -Sqrt[2] || x == -Sqrt[2] || x == -Sqrt[2] || x == -Sqrt[2] ||
> x == -Sqrt[2] || x == -Sqrt[2] || x == -Sqrt[2] || x == -Sqrt[2] ||
> x == -Sqrt[2] || x == -Sqrt[2] || x == -Sqrt[2] || x == -Sqrt[2] ||
> x == -Sqrt[2] || x == -Sqrt[2]
In[4]:= a=N[Sqrt[2]]
Out[4]= 1.41421
In[5]:= q1[x_] = PolynomialQuotient[q0[x], x-a, x]
2 3 4
Out[5]= 23170.5 + 16384. x - 162193. x - 114688. x + 527128. x +
5 6 6 7 6 8
> 372736. x - 1.05426 10 x - 745472. x + 1.4496 10 x +
6 9 6 10 6 11 6 12
> 1.02502 10 x - 1.4496 10 x - 1.02502 10 x + 1.0872 10 x +
13 14 15 16 17
> 768768. x - 621258. x - 439296. x + 271801. x + 192192. x -
18 19 20 21 22
> 90600.2 x - 64064. x + 22650. x + 16016. x - 4118.19 x -
23 24 25 26 27
> 2912. x + 514.774 x + 364. x - 39.598 x - 28. x +
28 29
> 1.41421 x + x
In[6]:= Roots[q1[x]==0, x]
Out[6]= x == -1.50284 || x == -1.48104 || x == -1.47697 || x == -1.46873 ||
> x == -1.46385 || x == -1.46084 || x == -1.44344 ||
> x == -1.41826 - 0.169774 I || x == -1.41826 + 0.169774 I ||
> x == -1.4036 || x == -1.36051 || x == -1.35636 || x == -1.3317 ||
> x == -1.33078 || x == -1.29556 || x == 1.31227 || x == 1.31612 ||
> x == 1.32213 || x == 1.36838 || x == 1.38377 || x == 1.42121 ||
> x == 1.4229 - 0.168219 I || x == 1.4229 + 0.168219 I || x == 1.42296 ||
> x == 1.441 || x == 1.45599 || x == 1.50241 || x == 1.50315 ||
> x == 1.50334
In[7]:=
Wat gebeurt hier? p(x) = (x^2 - 2)^15 is een polynoom met 15 nulpunten Sqrt[2] en 15 nulpunten -Sqrt[2]. Ik deel 1 factor weg, en plotseling ontstaat een polynoom met nulpunten die in absolute waarde tussen de 1.29556 en 1.50334 liggen (terwijl Sqrt[2] ongeveer 1.41421 is). Dus terwijl ik in 5 decimalen nauwkeurig reken is na een enkele stap zelfs de eerste decimaal al onbetrouwbaar. Bovendien zijn er nu plotseling complexe wortels, terwijl eerst alles reëel was.
Misschien is 5 decimalen wel niet genoeg. Hoe nauwkeurig is de machinearitmetiek hier eigenlijk?
In[7]:= $MachineEpsilon
-16
Out[7]= 2.22045 10
Hmm. Dus de machineprecisie is 16 decimalen. Laat ik de berekening overdoen met een nauwkeuriger versie van a.
In[8]:= a=N[Sqrt[2],20]
Out[8]= 1.4142135623730950488
In[9]:= q1[x_] = PolynomialQuotient[q0[x], x-a, x];
In[10]:= Roots[q1[x]==0, x]
Out[10]= x == -1.61944 || x == -1.606 || x == -1.54603 || x == -1.53514 ||
> x == -1.50407 - 0.210162 I || x == -1.50407 + 0.210162 I ||
> x == -1.45252 || x == -1.38079 - 0.215233 I ||
> x == -1.38079 + 0.215233 I || x == -1.28907 || x == -1.28512 ||
> x == -1.27824 || x == -1.2731 || x == -1.27267 - 0.150585 I ||
> x == -1.27267 + 0.150585 I || x == 0.838196 || x == 1.32177 ||
> x == 1.33355 || x == 1.3449 || x == 1.36164 || x == 1.36835 ||
> x == 1.42121 || x == 1.42296 || x == 1.42407 || x == 1.49447 ||
> x == 1.4968 - 0.556164 I || x == 1.4968 + 0.556164 I || x == 1.50353 ||
> x == 1.95727
Vreemd. Het lijkt wel slechter geworden. Nog nauwkeuriger dan.
In[11]:= a=N[Sqrt[2],40]
Out[11]= 1.414213562373095048801688724209698078570
In[12]:= q1[x_] = PolynomialQuotient[q0[x], x-a, x];
In[13]:= Roots[q1[x]==0, x]
-2 -2
Out[13]= x == -1.4 + 0. 10 I || x == -1.4 + 0. 10 I ||
-2 -2
> x == -1.4 + 0. 10 I || x == -1.4 + 0. 10 I ||
-2 -2
> x == -1.4 + 0. 10 I || x == -1.4 + 0. 10 I ||
-2 -2
> x == -1.4 + 0. 10 I || x == -1.4 + 0. 10 I ||
-2 -2
> x == -1.4 + 0. 10 I || x == -1.4 + 0. 10 I || x == -1.4 ||
-2 -2
> x == -1.4 || x == -1.4 + 0. 10 I || x == -1.4 + 0. 10 I ||
> x == -1.4 || x == 1.4 || x == 1.4 || x == 1.4 || x == 1.4 || x == 1.4 ||
-3
> x == 1.4 || x == 1.4 || x == 1.41 + 0. 10 I ||
-3 -3
> x == 1.41 + 0. 10 I || x == 1.41 + 0. 10 I ||
-3 -3
> x == 1.41 + 0. 10 I || x == 1.4 || x == 1.42 + 0. 10 I ||
-3
> x == 1.42 + 0. 10 I
Aha. Dus de vorige berekening werd door Mathematica nog in machineprecisie gedaan, en zonder aarzelen drukte hij 5 decimalen af. Maar nu ik begon met 40 significante cijfers houdt Mathematica precies bij wat de nauwkeurigheid van zijn resultaten zijn, en deze wortels hebben een nauwkeurigheid die niet groter is dan 1 of 2 decimalen. (Bij een a met 100 cijfers precisie komen er wortels als -1.41421 + 0. 10^(-6) I met 6 cijfers precisie.)
Eerste conclusie: heel kleine variaties van de coefficiënten van een polynoom kunnen heel grote variaties in de ligging van de nulpunten ten gevolge hebben. In het bijzonder meervoudige nulpunten zijn gevaarlijk.
Tweede conclusie: numeriek werk vergt grote voorzichtigheid. Een argeloos wiskundige begaat als hij met numeriek werk begint talrijke grove blunders. Algoritmen die wiskundig gezien equivalent zijn kunnen numeriek heel verschillend gedrag vertonen.
Numerieke wiskunde is dan ook een afzonderlijk vak geworden.
Hoe moet je eigenlijk wortels vinden van een veelterm, of eigenwaarden van een matrix? Daar zijn allerlei manieren voor, en zoals gezegd hoort dat in de numerieke wiskunde thuis. Maar laat ik hier een enkele manier beschrijven die zowel theoretisch als practisch van belang is.
Als je een polynoom p hebt, en twee waarden a en b met p(a) < 0 < p(b), dan is het makkelijk om een nulpunt van p te bepalen, zo precies als we maar willen: Kijk naar c = (a+b)/2. Als p(c) > 0 dan is er een nulpunt tussen a en c, als p(c) < 0 dan is er een nulpunt tussen c en b en als p(c) = 0 dan hebben we het nulpunt al gevonden. Dus bisectie is een heel stabiel algoritme, al is het misschien niet het snelste; elke tien bisecties leveren drie decimalen meer op.
Blijft de vraag: hoe moet ik beginnen? Als ik allerlei waarden a probeer, en telkens is p(a) > 0, zijn er dan wel reele nulpunten? Tussen twee opeenvolgende nulpunten van de afgeleide p'(x) ligt hooguit 1 nulpunt van p(x), dus als ik alle nulpunten van p' zou kennen was ik klaar. En om die te vinden is het voldoende om naar p'' te kijken...
Deze overwegingen leiden tot het volgende algoritme (van Sturm):
Zij p_0(x) = p(x) en p_1(x) = p'(x). Als p_i(x) bekend is voor i=0,1,...,m-1, dan zij p_m(x) het tegengestelde van de rest by deling van p_{m-2}(x) door p_{m-1}(x). Als p(x) graad n heeft, dan heeft p_i(x) (hooguit) graad n-i, en is dus p_n(x) een constante. Zij n(x) het aantal tekenwisselingen in de rij p_0(x), p_1(x), ..., p_n(x) (waarbij nullen weggelaten worden). Als a en b zelf geen nulpunten van p(x) zijn, dan is het aantal verschillende nulpunten van p(x) in het interval [a,b] gelijk aan n(a)-n(b).
Laat bijvoorbeeld p(x) = (x+1)(x-1)^2 = x^3 - x^2 - x + 1. We vinden p_0 = p en p_1(x) = 3x^2 - 2x - 1 en p_2(x) = (8/9)*(x-1) en p_3(x) = 0. Nu vinden we voor x=-2: -,+,-,0 en voor x=-1: 0,+,-,0 en voor x=0: +,-,-,0 en voor x=1: 0,0,0,0 en voor x=2: +,+,+,0. Dus n(-2) = 2 en n(0) = 1 en n(2) = 0 Dus in [-2,2] liggen twee verschillende wortels, één in [-2,0] en één in [0,2]. Nu levert weer herhaalde bisectie de nulpunten.
Opgave Bewijs de stelling van Sturm.
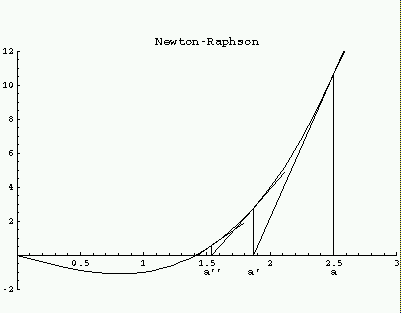
In de vorige paragraaf hadden we een zeer stabiel maar vrij traag algoritme om nulpunten te vinden: na tien iteraties hadden we drie decimalen meer. Het kan ook veel sneller: met elke iteratie verdubbelt het aantal decimalen. Hoe? Als a een gok voor een nulpunt van een functie f(x) is, teken dan de raaklijn aan de grafiek van f in het punt (a,f(a)), kijk waar die raaklijn de x-as snijdt, en dat is een verbeterde gok a' voor dat nulpunt. Kortom:
a' = a - f(a)/f'(a)
Herhaal nu dit proces met a' en vind a''. Enz. Hieronder een illustratie benevens de Mathematica invoer die dit plaatje genereerde.

Opgave Ga na dat dit algoritme kwadratisch convergeert als f' niet nul is in de buurt van het gezochte nulpunt, en we voldoend dicht bij het gezochte nulpunt beginnen, en f(x) in de buurt van het nulpunt in een Taylor reeks ontwikkeld kan worden.
Bij meervoudige nulpunten werkt deze methode slecht: als f(x) = x^2 en we hebben a als benadering van het nulpunt, dan is a' = a/2, en de procedure is niet sneller dan bisectie.
Bij functies die zich in de buurt van het nulpunt niet als een gehele macht van x gedragen is het effect nog veel droeviger: Als f(x) = x^(1/3) dan is a' = -2a zodat elke stap de afstand tot het nulpunt verdubbelt.
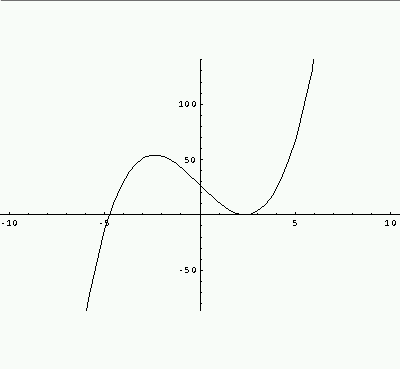
Ook bij mooie polynomen zonder meervoudige nulpunten kun je door Newton-Raphson gefopt worden. Bijvoorbeeld, als p(x) = x^3 - 17x + 27 en ik begin bij 0, dan zijn de volgende iteraties 1.58824, 2.01297, 2.20624, 2.30333, 2.36174, en dat ziet er hoopvol uit: p(2.36174) = 0.02377 is al tamelijk klein. Maar bij voortzetten van de iteratie: 2.45092, 2.39504, 2.28582, 2.34952, 2.41345, 2.35215, 2.41923, 2.36179 komen we na acht stappen bijna op hetzelfde punt terug.
Opgave Waarom convergeert Newton-Raphson hier niet?
Hieronder de grafiek van p(x).