
Een routine heet recursief als hij zichzelf aanroept.
In sommige computertalen kan dat niet (bijvoorbeeld in PDP8 assembler
schrijft JMS IETS het aanroepadres weg op een vaste plek, aan het begin
van de routine IETS, en als die routine zichzelf zou aanroepen
zou dat terugkeeradres overschreven worden). In de meeste talen is dit
echter geen probleem. Recursie wordt geďmplementeerd met behulp van een
stapel (stack), en als je herhaaldelijk een terugkeeradres op de stack
gooit, dan ligt het adres dat je nodig hebt bij het verlaten van de
routine altijd bovenop.
Soms kun je kiezen tussen recursie en iteratie (herhaling). Bijvoorbeeld voor het berekenen van een grootste gemene deler kun je de iteratieve C code
int ggd(int m, int n) {
int a;
if (m < 0) m = -m;
if (n < 0) n = -n;
while(m != 0) {
a = n%m; /* % geeft de rest bij deling */
n = m;
m = a;
}
return n;
}
int ggd2(int m, int n) {
if (m == 0)
return n;
else
return ggd2(n%m, m);
}
Opgave Zijn beide routines correct? Wat is het verschil in resultaat? In snelheid? In geheugengebruik?
Opgave Schrijf een iteratieve en een recursieve versie
van de routine binom(m,n) die de binomiaalcoefficiënt n-kies-m
uitrekent.
Merk op dat recursie een bodem moet hebben: een routine als
int geenfaculteit(int n) {
return n*geenfaculteit(n-1);
}
Bij bovenstaande voorbeelden is er sprake van nep-recursie die moeiteloos door iteratie vervangen kan worden. Een interessanter gebruik is dat bij het aflopen van een boom.
Een voor de hand liggend voorbeeld van een boom die je zou willen aflopen is de boom van mogelijke voortzettingen van een schaak- of dam- of go-partij. "Als ik dit doe, en hij doet dat, en ik doe ..., dan ..., maar als hij dŕt doet, en ik ..., dan ..."
Het volgende programma speelt perfect schaak, en dam, en go, en nog zo wat van die spelen.
/* Bepaal de waarde van de stand: 1 als ik win, 0 bij remise, -1 bij verlies */
/* Hierbij is `ik' de speler die aan zet is. */
int
value() {
int i;
bool candraw;
move z;
if (game_is_over_already)
return I_won ? 1 : I_lost ? -1 : 0;
candraw = FALSE;
create_list_of_all_legal_moves;
for_each_legal_move z {
do_move(z); /* alleen in gedachten, niet op het echte bord */
i = value(); /* recursieve aanroep */
undo_move(z); /* maak uitgeprobeerde zet weer ongedaan */
if (i == -1) /* verliest hij? */
return 1; /* dan win ik! */
if (i == 0) /* wordt het remise? */
candraw = TRUE; /* onthoud dat er een remisevariant is */
}
return candraw ? 0 : -1;
}
/* Doe de beste zet in deze stand */
/* Hetzelfde werk als hierboven, alleen willen we nu niet alleen
de uitslag, maar ook de beste zet weten. Deze routine is niet recursief. */
void
move() {
int i;
move goodmove = NONE;
move z;
create_list_of_all_legal_moves;
for_each_legal_move z {
do_move(z); /* alleen in gedachten, niet op het echte bord */
i = value();
undo_move(z); /* maak uitgeprobeerde zet weer ongedaan */
if (i == -1) { /* verliest hij? */
goodmove = z; /* dan doen we dit! */
break; /* en we hoeven niet verder te zoeken */
}
if (i == 0) /* wordt het remise? */
goodmove = z; /* laten we deze zet onthouden */
}
if (goodmove != NONE)
play_move(goodmove);
else
resign; /* geef op - iedere zet leidt tot verlies */
}
Oefening Vul de details in zodat dit een correct werkend programma wordt. Speel boter-kaas-en-eieren. Pas het programma aan zodat het voor de snelste winst kiest, en laat het niet opgeven maar voor de langzaamste remise of verlies kiezen.
Weliswaar speelt dit programma perfect, maar als we er tegen willen schaken hebben we wat geduld nodig. Het is niet zeker dat het voor het einde van het heelal de eerste zet zal doen.
Hmm. Dat betekent dat we de recursie wat moeten beperken. Niet alle mogelijke varianten tot aan het einde toe aflopen. Maar als we maar een stukje van een variant bekijken hebben we een evaluatiefunctie nodig die zegt hoe goed we er voor staan. Het maken van goede schaakprogramma's is voornamelijk het maken van een goede evaluatiefunctie.
(Een redelijke gok is: tel materiaal: Koning 10000, Dame 90, Toren 45, Loper 30, Paard 30, Pion 10, en de som van mijn materiaal min de som van mijn tegenstanders materiaal, dat is hoe goed ik er voor sta. Maar natuurlijk... Al sta ik een dame voor, kan er toch mat in drie dreigen. Een goed schaakprogramma heeft talrijke heuristieken, en geeft nog wat extra plus of min puntjes voor het gerokeerd hebben, voor het loperpaar, voor controle over het centrum, voor bewegelijkheid, voor pionnenstructuur, enz. enz.)
(Aan de andere kant, het hebben van een grote batterij heuristieken kost veel tijd, zodat de evaluatiefunctie duur wordt. Dan kan het weer interessant worden om één zet dieper te rekenen, en terug te gaan naar een veel simpeler evaluatiefunctie. Ik geloof dat Deep Blue, het programma dat van Kasparov won, voornamelijk botte rekenkracht is, en geen subtiele evaluatiefunctie heeft.)
Bij het aflopen van de boom van mogelijke spelverlopen kunnen we veel tijd besparen door de boom te snoeien. Als ik al gezien heb dat op een zet van mij de tegenstander een verpletterend antwoord heeft, dan hoef ik niet na te denken wat hij nog meer zou kunnen doen, dan is mijn zet toch al afgekeurd. Dit soort overwegingen leidt tot alpha-beta pruning. Hierbij worden varianten die aantoonbaar geen invloed op het resultaat hebben weggelaten.
int
eval() {
int w;
/* Bepaal de waarde van de stand. Stop hier al je
inzicht over het spel in. */
...
return w;
}
/* Bepaal de waarde van de stand als ik niet verder dan d zetten
vooruit mag kijken. Als de waarde lager is dan alpha dan ben
ik er niet in geďnteresseerd, dan weet ik wel iets beters.
Als de waarde hoger wordt dan beta dan zou ik dat wel leuk vinden,
maar dan kiest mijn tegenstander nooit deze variant, dus dan komen
we hier helemaal niet. */
int
value(int alpha, int beta, int d) {
int i;
int bestsofar;
if (game_is_over_already)
return I_won ? beta : I_lost ? alpha : 0;
if (d <= 0)
return eval(); /* schat hoe goed de stand is */
bestsofar = alpha;
create_list_of_all_legal_moves;
for_each_legal_move z {
do_move(z); /* alleen in gedachten, niet op het echte bord */
bestsofar = -value(-beta, -bestsofar, d-1);
undo_move(z); /* maak uitgeprobeerde zet weer ongedaan */
if (bestsofar >= beta)
return beta;
}
return bestsofar;
}
/* Doe de beste zet (volgens eval na DEPTH zetten) in deze stand */
void
move() {
int i;
int bestsofar = -INFINITY;
move goodmove = NONE;
move z;
if (game_is_over_already) {
print(result);
exit;
}
create_list_of_all_legal_moves;
for_each_legal_move z {
if (goodmove == NONE)
goodmove = z; /* er is in elk geval een mogelijke zet */
do_move(z); /* alleen in gedachten */
i = -value(-INFINITY, -bestsofar, DEPTH); /* beoordeel stand */
undo_move(z); /* maak uitgeprobeerde zet weer ongedaan */
if (i > bestsofar) {
bestsofar = i;
goodmove = z; /* onthoud de beste zet totdusver */
}
}
if (goodmove == NONE)
cannot_move; /* pas? pat? verloren? Hangt van het spel af */
else
play_move(goodmove); /* doe de zet */
}
Opgave In welke regel hierboven geschiedt het snoeien?
Alpha-beta pruning werkt het effectiefst als de beste zetten het eerst worden uitgeprobeerd. (Maar hoe weet je welke dat zijn??) Bij spelen waarbij verwisseling van zetten tot dezelfde stand kan leiden is het soms nuttig al bekeken standen te bewaren (in een enorme hash-tabel bijvoorbeeld), en/of met transpositietabellen te herkennen dat een stand al eerder is bekeken.
Doorrekenen tot op een vaste diepte is geen goed idee. In een saaie stand moet je misschien eerder ophouden, en als er net geslagen is, of als de koning schaak staat, nog wat verder rekenen om te zien hoe het verder gaat. Als de boom sterk vertakt (telkens veel zetten mogelijk) dan kun je niet zo diep gaan, maar bijvoorbeeld met dammen, waar slaan verplicht is, kunnen er lange, bijna niet-vertakkende combinaties voorkomen, en die wil je zeker tot het einde doorrekenen.
Een probleem dat moeilijk te vermijden is, is het `horizon' effect. Als een damprogramma een dam op drie schijven waardeert, zodat promotie mijn stelling twee schijven meer waard maakt, en in sommige varianten haal ik een dam, dan zal menig programma een steen offeren om dat probleem over de horizon te schuiven: 1 steen verloren is nog altijd beter dan 2. Maar de volgende zet dreigt weer hetzelfde probleem, en weer offert het programma. Zo gaat het door totdat er niets meer te offeren valt en het programma totaal verloren staat. Met schaken gebeurt natuurlijk hetzelfde. Een programma dat een toren voorstaat, maar een toren moet offeren om niet na vijf zetten mat te lopen, zal vrolijk een paard, en een loper en nog een loper en dan pas die toren offeren als elk offer het probleem over de recursiehorizon wegduwt en de evaluatiefunctie het probleem niet ziet. Dit is een probleem in het samenspel tussen recursiediepte en evaluatiefunctie, en bij een goede functie treedt het niet (of veel minder) op.
Bij het maken van een volledige eindspel data base, zeg van K+P tegen K+T, werk je niet in de tijd maar in de ruimte: maak een lijst van alle mogelijke standen. Leid uit alle standen met mat in 0 de standen met mat in 1 af, daaruit die met mat in 2, enz. Als er niets meer bij komt ben je klaar, en zijn alle andere standen remise.
Probleem
Ruim twintig jaar geleden schreef op tweede Paasdag
een damprogramma waar ik van verloor. (Ik kan namelijk niet dammen.)
Schrijf een sterker programma. Mijn programma is beschikbaar
in het linux-intel-bin directory.
Recursie komt ook buiten programma's voor.
In Nederland is de Droste verpleegster spreekwoordelijk. (Op een blik Droste cacaopoeder staat een verpleegster afgebeeld met een dienblad, en op dat dienblad staat een blik Droste cacaopoeder waarop een verpleegster te zien is die...)

dandy (dendie) m [-'s] fat.
fat [-ten] dandy.
(Prisma Woordenboek Nederlands, 1955)
Een definitie kan recursief zijn. De naam van het systeem GNU staat voor `GNU, not Unix'. Dit is een recursie zonder bodem.
`Meta' is een prefix dat ongeveer `over' betekent. `Metawiskunde' is de theorie die over wiskunde nadenkt; in de metawiskunde gaat het over de manier waarop in de wiskunde stellingen worden bewezen, over eigenschappen van bewijzen, enzovoort. Natuurlijk is de metawiskunde ook een theorie en dat betekent dat je over de eigenschappen van deze theorie kunt nadenken en metametawiskunde bedrijven.
Als je van een geest drie wensen mag doen dan verwacht hij dat je vraagt om een glas bier, of om duizend gulden, of om mooi weer. Maar als je vraagt om nog honderd wensen te mogen doen dan is dat een metawens, een wens over het wensen. En als onder die honderd wensen ook metawensen zouden kunnen voorkomen dan is het zelfs een metametawens. En ...
In Gödel, Escher, Bach van Douglas Hofstadter, moet de geest aan de metageest toestemming vragen voor het vervullen van metawensen. En die moet de metametageest raadplegen als het om metametawensen gaat... Hij raadpleegt GOD.
[Achilles:] Before I make my wish, would you mind telling me who - or what - GOD is?
[Genie:] Not at all. "GOD" is an acronym which stands for "GOD Over Djinn". The word "Djinn" is used to designate Genies, Meta-Genies, Meta-Meta-Genies, etc. It is a Typeless word.
[Achilles:] But - but - how can "GOD" be a word in its own acronym? That doesn't make any sense!
[Genie:] Oh, aren't you acquainted with recursive acronyms? I thought everybody knew about them. You see, "GOD" stands for "GOD Over Djinn" - which can be expanded as "GOD Over Djinn, Over Djinn" - and that can, in turn, be expanded to "GOD Over Djinn, Over Djinn, Over Djinn" - which can in its turn, be further expanded... You can go as far as you like.
[Achilles:] But I'll never finish!
...
Bij het beschrijven van hoe je een geheel getal schrijft, zou je de definitie
<nietnulcijfer> :: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<cijfer> :: 0 | <nietnulcijfer>
<nietnulgetal> :: <nietnulcijfer> | <nietnulgetal><cijfer>
<getal> :: 0 | <nietnulgetal>
De recursie hier was van het flauwe soort, eenvoudig door iteratie te vervangen: nietnulgetal wordt beschreven door de reguliere expressie [1-9][0-9]* .
(Maak je geen zorgen als je de details van deze definities niet begrijpt; hopelijk is het algemene idee duidelijk. Definities in de eerste stijl heten definities in BN (Backus-Naur) vorm, en zijn bekend geworden omdat de Algol60 grammatica zo geformuleerd was. De | staat voor `of', en de :: lees je als `is een'. Dus: een getal is 0 of is een nietnulgetal. Enz. Reguliere expressies zijn bekend uit de Unix editor ed. Hier staat * voor `0 of meer herhalingen van het vorige symbool' en [A-Z] voor `een willekeurig symbool met ASCII code tussen die van A en die van Z. Gelukkig hebben letters en cijfers opeenvolgende ASCII codes, dus dit doet (in het Engels) wat je verwacht.)
In het algemeen zullen definities van programmeertalen ook ingewikkelder vormen van recursie bevatten.
Bijvoorbeeld, goed-geneste haakjesparen leveren uitdrukkingen zoals ()((()())()). Een grammatica zou kunnen zijn:
<hh> :: | (<hh>) | <hh><hh>
Even terzijde. Hoeveel van die correcte haakjesuitdrukkingen zijn er met n haakjesparen? Bij n=0 is er één: . Bij n=1 is er ook één: (). Bij n=2 zijn er twee: ()() en (()). Bij n=3 zijn er vijf: ()()(), (())(), ()(()), (()()), ((())). Bij n=4 zijn er veertien: ()()()(), (())()(), ()(())(), (()())(), ((()))(), ()()(()), (())(()), ()(()()), ()((())), (()()()), ((())()), (()(())), ((()())), (((()))). Wat is de algemene formule? Beschouw een haakjesuitdrukking als een trap: ( is een stap omhoog, en ) is een stap omlaag. Een haakjesuitdrukking is correct als we op de grond beginnen en eindigen, en ondertussen nooit onder de grond geweest zijn. (In de vijf voorbeelden bij n=3 kunnen we het niveau aangeven: 0(1)0(1)0(1)0, 0(1(2)1)0(1)0, 0(1)0(1(2)1)0, 0(1(2)1(2)1)0, 0(1(2(3)2)1)0.) Als we er in gedachten nog een haakje voor zetten, dan krijgen we trappen met n+1 stappen omhoog en n stappen naar beneden, die beginnen met een stap omhoog en nooit meer op de grond komen. Het totale aantal uitdrukkingen met n+1 keer ( en n keer ) is (2n+1 kies n). Maar elk van die uitdrukkingen heeft een unieke cyclische verschuiving die correct is. Bijvoorbeeld, bij n=4 is )(())((() fout: met bijgeschreven niveaux is het 0)-1(0(1)0)-1(0(1(2)1, en we moeten beginnen na het laatste punt waar een negatieve waarde stond: ((())(()). De conclusie is dat het aantal correcte haakjesuitdrukkingen precies (2n+1 kies n) / (2n+1) is.
Deze getallen, en deze haakjesuitdrukkingen, komen op talloze plaatsen in de wiskunde voor. Bijvoorbeeld geeft dit het aantal manieren om een convexe (n+2)-hoek met diagonalen in stukken te verdelen.
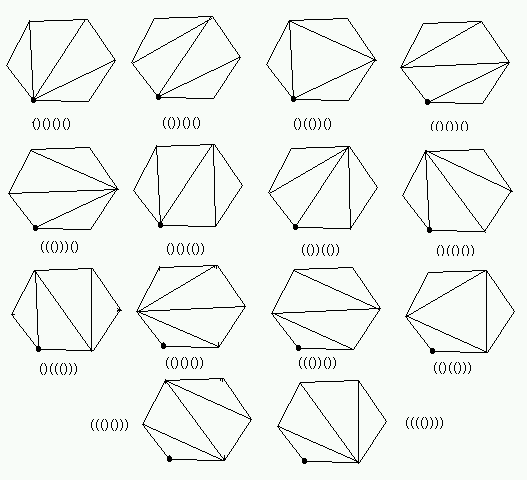
Hier de correspondentie. (Begin met de dikke stip, en loop rond met de klok mee. Schrijf bij elke kant een ( totdat voor het eerst een driehoek gevormd wordt. Schrijf dan ), en haal de driehoek weg en ga verder met de veelhoek die één hoekpunt minder heeft.)
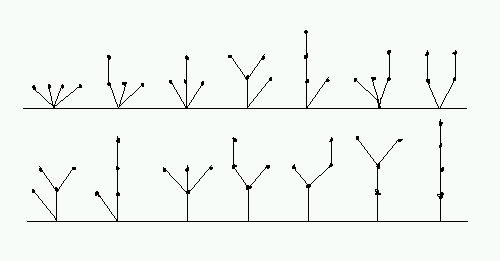
Maar ook geeft het het aantal in het vlak ingebedde gewortelde bomen met n knopen (waarbij de wortel niet meetelt). De correspondentie zal duidelijk zijn.
Maar ook geeft het het aantal binaire bomen met n+1 bladeren. Inderdaad, een binaire boom met n+1 bladeren kan opgevat worden als een volledig van haakjes voorziene vermenigvuldiging van n+1 dingen, zoals ((ab)(c(de))). Om hieruit een in het vlak ingebedde gewortelde boom af te leiden laten we alle ( weg: ab)cde))) en voegen nu weer haakjes toe: a(b)(c(d(e))) waarbij we nu alle letters kunnen vergeten: ()((())). (Dus het toevoegen gaat als volgt: zet een haakje openen zo dicht mogelijk bij het haakje sluiten, maar zo dat er een letter op volgt.) Het plaatje hieronder geeft dit en nog een wat groter voorbeeld.
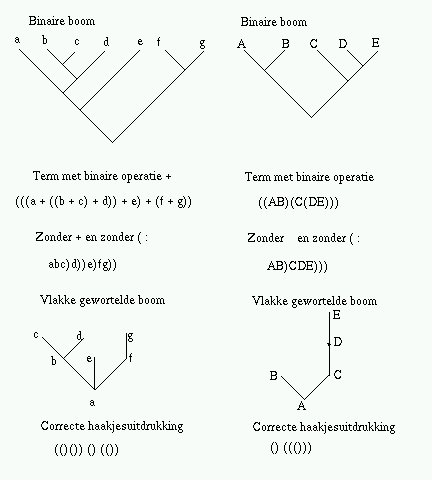
Opgave Wat zijn de veertien binaire bomen met vijf blaadjes? (Of, als je dit per epost inlevert: Wat zijn de veertien volledig van haakjes voorziene vermenigvuldigingen van 5 dingen?)
Een recursieve definitie zonder keuze (zonder `of') aan de rechterkant kan gelezen worden als herschrijfsysteem. Nu is het niet erg als er geen bodem is - de verschillende vormen worden gezien als stadia in de tijd. Begin met een beginsymbool, en vervang bij elke iteratie wat links staat door wat rechts staat. Bijvoorbeeld, bij een herschrijfsysteem met regels X=YZ, Y=ZXZY, Z= vinden we uitgaande van X achtereenvolgens YZ, ZXZY, YZZXZY, ZXZYYZZXZY, ...
Vaak wordt hier een biologische betekenis aan toegekend, en is de bedoeling van zo'n herschrijfsysteem om een plant of eenvoudig dier te beschrijven. (Bijvoorbeeld zou X=YY kunnen betekenen dat een oude cel zich deelt in twee jonge cellen, en Z= zou het overlijden van een cel kunnen weergeven. De definitie van GOD hierboven zou een grasspriet kunnen beschrijven met een pluim boven een alsmaar langer wordende stengel.) In dit verband worden de herschrijfsystemen vaak Lindenmayersystemen genoemd. (Inderdaad ziet een tak van een boom er weer uit zoals de boom zelf - het is duidelijk dat bomen een recursieve structuur hebben. Vergelijk ook het beeld voor de ingang van de wiskundebibliotheek.)
In eerste instantie lijkt het alsof we zo alleen 1-dimensionale patronen vinden, maar als we symbolen `linksaf' en `rechtaf' toelaten dan ontstaan interessante 2-dimensionale plaatjes. Het bekendste voorbeeld is misschien de drakenkromme, gegeven door X=XLY, Y=XRY. Wat andere voorbeelden.
Een andere manier om bomen weer te geven is met haakjesstructuren als in de vorige paragraaf. Deze tak van sport wordt tegenwoordig veel gebruikt bij computerproductie van landschapsbeelden. Voor mooie plaatjes, zie Prusinkiewics & Lindenmayer, The algorithmic beauty of plants.
De wiskundig-technische definitie van fractals is heel anders, en heeft niets met recursie te maken, maar veel fractals worden met een recursief recept gedefinieerd. Zo'n recept zorgt er voor dat de figuur er in het klein overal net zo uitziet als in het groot. (Als het recept niet-linear is, dan vind je in het klein vervormde stukken van de grote figuur.) Bekende voorbeelden zijn de Juliaverzamelingen en de Mandelbrotverzameling. Hieronder vier plaatjes; elk is een uitvergroting van een deel van de vorige.




De Mandelbrotverzameling ontstaat als volgt: kijk naar de afbeelding die een punt z in het complexe vlak stuurt naar z' = z^2 + c voor zekere constante c, en herhaal die afbeelding. (Dus: a gaat naar (a^2 + c), en dat gaat weer naar (a^2 + c)^2 + c, ...) Wat gebeurt er op de lange duur? Als |z| flink groot is (bijvoorbeeld groter dan |c|+1), dan is |z'| nog groter, en het punt verdwijnt naar oneindig. Maar voor kleine z hangt het heel erg van c af wat er gebeurt. Definieer de Mandelbrotverzameling M (het zwarte gedeelte van de plaatjes hierboven) als de collectie van alle c waarvoor met het startpunt 0 de rij begrensd blijft, niet naar oneindig loopt. Bijvoorbeeld zit 0 in M: 0, 0, ... is begrensd; en -1 zit in M: 0, -1, 0, -1, ... is begrensd, en -2 zit in M: 0, -2, 2, 2, 2, ... is begrensd, en 1/4 zit in M: 0, 1/4, 5/16, 89/256, ... wordt nooit groter dan 1/2, en inderdaad het hele reele interval [-2, 0.25] zit in M.
Opgave Laat zien dat de doorsnede van M met de reele rechte precies het interval [-2, 0.25] is.
De cardioide-achtige figuur rechts in het eerste plaatje heeft zijn linker zijkant bij -3/4, en is rechts ingesneden tot 1/4. De kleurbanen worden gedefinieerd door te kijken na hoeveel iteraties een punt `ver weg' is (zeg, absolute waarde groter dan 100 heeft).
De Mandelbrotverzameling ontstaat door bij 0 te beginnen en voor telkens andere c te kijken wat er gebeurt. Je kunt ook c vast kiezen, en voor alle z kijken wat er gebeurt. De verzamelingen die je zo vindt heten Juliaverzamelingen, een voor elke c. Hieronder een paar voorbeelden.






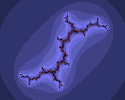


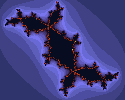


Als c groot is, ver buiten M, dan is de bijbehorende Juliaverzameling J(c) heel dun, een paar kleine losse eilandjes, zoals in het eerste plaatje. Als c=0 dan is kennelijk J(c) een massieve cirkel met straal 1. Het laatste plaatje hoort bij een c dicht bij 0. Bij c=i vinden we een draadachtige verzameling (zie plaatje 7). Interessante J(c) zoals het voorlaatste plaatje ontstaan door c heel dicht bij de rand van M te kiezen. Met c binnen M ontstaat een samenhangende figuur, met c buiten M een onsamenhangende (volgens de stelling van Fatou en Julia, 1919).
Opgave Laat zien dat de Juliaverzameling J(c) invariant is onder de afbeelding die z op z^2 + c afbeeldt.
`Recursie' komt uit het Latijn: `recurrere' (teruglopen), afgeleid van `currere' (lopen, rennen).
We kennen talloze woorden hiervan afgeleid: `curriculum' (loopbaan), Frans `courir' (rennen), `corridor' (gang), `au secours!' (help!), Spaans `correo' (post), Engels `current', `currency', `course', `coarse', Ned. koerier, cursief, cursus, cursor (`loper' op het scherm), enz. enz. Met andere voorzetsels: concurrentie, concours, discours, escorte, excursie, occurrence (gebeurtenis), enz. enz.
De bijbehorende indoeuropese wortels zijn *kers (lopen) en *krsos (wagen).
Volgens de regelen der kunst levert de indoeuropese *k in de Germaanse talen een h op. (Bijvoorbeeld: Lat. `cor', gen. `cordis', Fra. `coeur', is familie van Ned. `hart'. Lat. `centum' is familie van Ned. `honderd'. Lat. `canis' is familie van Ned. `hond'. Lat. `cornu' is familie van Ned. `hoorn'. Lat. `collis', `culmen' is familie van Ned. `heuvel'. Enz.) Rijst de vraag of we woorden van deze wortels hebben die niet aan het Latijn ontleend zijn. Ik houd het er op dat het Engelse `hurry' hiervandaan komt.
Ook is het denkbaar dat ons `ros' (oudsaksisch `hros', Engels `horse') hiervandaan komt.
We hebben ook de `kar' uit het Keltisch of uit het Latijn `carrus'. (Met aanverwanten, zoals Engels `car', `chariot', `charge', `cargo' enz.)
Via Oost-Europa komt `huzaar' (uit Hong. `huszár' (vrijbuiter) uit Serv. `husar' uit Byz. Gr. `koursor' uit Lat `cursor' (renner)).