Prev Up Next

Forcing chains

Earlier, we considered chains of equal pairs, and observed that the values must alternate. Let us now consider chains of the form ab-bc-cd-...-xy-yz, of pairs where the second element of each pair (except the last) equals the first element of the next pair. If the field corresponding to the first pair has the second value b, then the next has the second value c, etc., and the last has the second value z. If that is a contradiction - for example because the chain was a cycle, the first and last pair belong to the same square, and the last pair is ba - then the field corresponding to the first pair must be a.

Terminology The forcing chains described above are called 'simple bivalue xy-chains'.

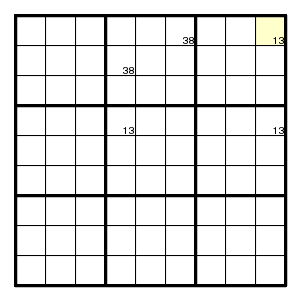
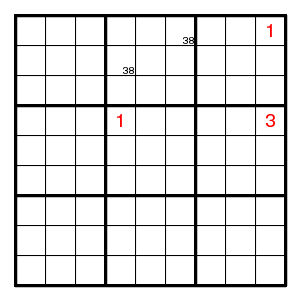
For example, the cycle 13-31-13-38-83-31 starting and ending in the yellow square, forces the digits in red:

Use of the cycle 83-31-15-58-83-38:

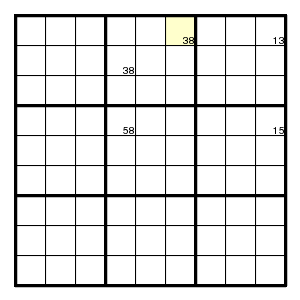
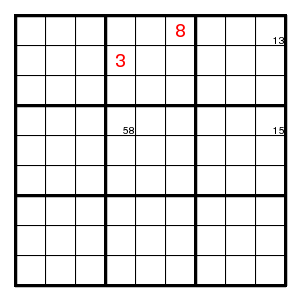
Use of the cycle 26-68-86-65-56-62:

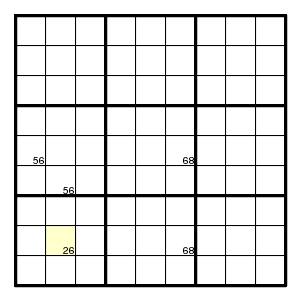
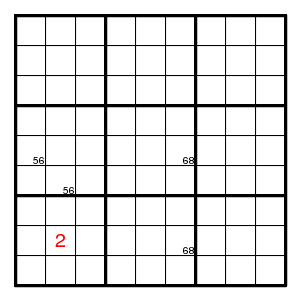
A more general way of getting a contradiction, is with a position that is both first and last element of the chain and may have more than two possible values. A chain of the form Xa-ab-bc-...-za-aX proves that the first element is not a.

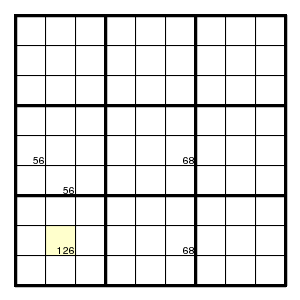
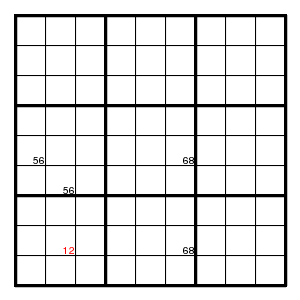
A rather common version is the short chain Xa-ab-bc-cd-dX. For example,

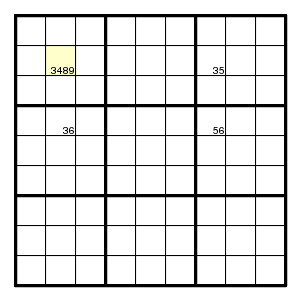
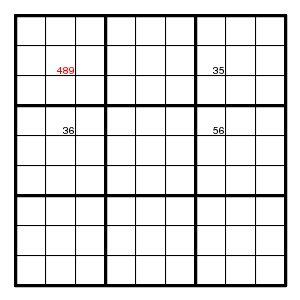
Terminology This last argument is known as 'XY-wing'.

Forcing chains and three possibilities

Consider

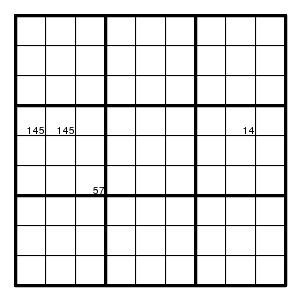
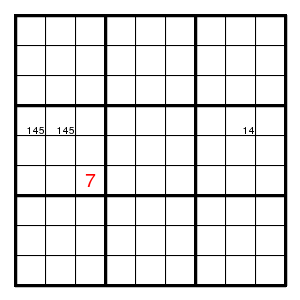
The yellow square cannot be 1, hence must be 2.

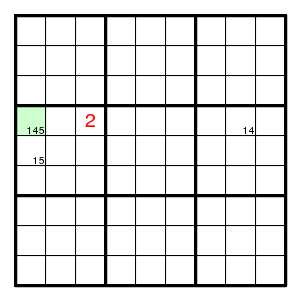
This can be described as a set of forcing chains *5-51-12 and *4-41-12 and *1-12 all starting in the green square. Since the green square has value 1 or 4 or 5, the yellow square is forced to be 2 in all cases.

Of course it doesn't play a role that the yellow square had only two possible values. The argument just shows that it cannot be 1.

Terminology This argument is known as 'XYZ-wing'.

Here a somewhat similar situation:

Prev Up Next