Suppose we have a chain A=B-C=D (or A=B-C=D-E=F etc.), where every odd link is a pair (for the same digit d) and the remaining links are ordinary adjacencies. Then a common neighbour of the two ends of the chain is not d.
(Indeed, if for example the chain is A=B-C=D-E=F and X is adjacent to both A and F so that we have X-A=B-C=D-E=F-X, and X is d, then A is not, so B is, so C is not, ..., so F is, so X is not.)
Terminology The forcing chains described above are called 'x-cycles'.
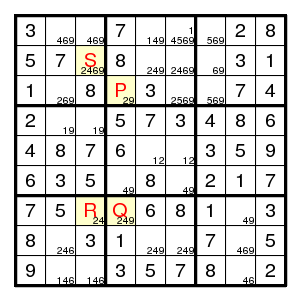
Look at an example.


The starting configuration leads without problems to the situation on the right. It has the chain P=Q-R=S for the digit 2 indicated in yellow. Therefore the three common neighbours of P and S do not have a 2. We obtain
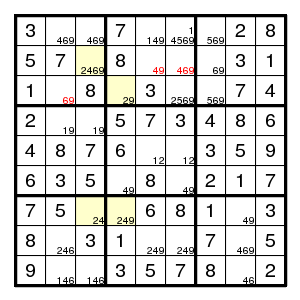
and the rest is straightforward.
(There was one more application in the same diagram, also for the digit 2, namely (8,2)=(3,2)-(3,4)=(7,4) where the three positions (7,3), (8,5), (8,6) are common neighbours of the endpoints, and consequently cannot be 2.)
Terminology This argument (for a chain of length 3) is also known as 'Turbot Fish'.