Prev Up Next

Uniqueness

A properly formulated Sudoku puzzle has a unique solution. One can assume that a given puzzle actually is properly formulated, and use that in the reasoning, to exclude branches that would not lead to a unique solution.

The BUG principle

Theorem (cf. nick67) Suppose one writes some (more than 0) candidate numbers in some of the initially open cells of a given Sudoku diagram, 0 or 2 in each cell, such that each value occurs 0 or 2 times in any row, column, or box. Then this Sudoku diagram has an even number of completions that agree with at least one of the candidates in each cell where candidates were given. In particular, if the Sudoku diagram has a unique solution, then that unique solution differs from both candidates in at least one cell.

Terminology It seems that BUG abbreviates 'Bivalue Universal Grave'.

Proof Given any completion of the given diagram that has one of the two candidate values in each cell where candidates were given, make a new completion by replacing each candidate number by the other candidate in that cell.

Uniqueness Argument

As an application one has the Uniqueness Argument: Whenever one has a nonempty set of initially open cells, and two candidates at each of those cells, such that among these candidates each value occurs zero or two times in each row, column and block, then the actual solution differs in at least one cell from both candidates.

People talk about destroying uniqueness rectangles, but such a thing is impossible. The only requirement on the candidates is that they are in initially open cells, not that they have anything to do with your current solving state. On the other hand, this means that the Uniqueness Argument gets progressively weaker if one does not remember the initial state and just has the current state.

Global BUG example

tso gave the following example.

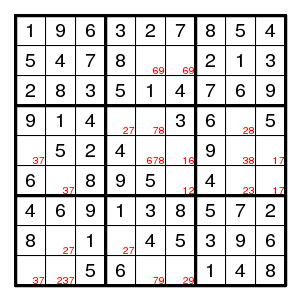
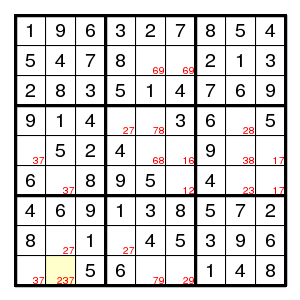
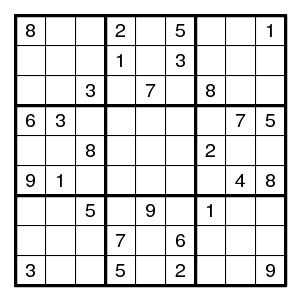
Here the (5,5) position cannot be 7 because of the 37 pair to the left and the 17 pair to the right. If the yellow square is not 7, then we obtain a situation where the BUG theorem applies. That is, there is an even number of solutions, presumably zero, where the yellow square is not 7. So, if this is a proper puzzle (which it happens to be), the yellow square is 7.

Local application

The simplest example is of course a rectangle meeting two boxes, with the same two possibilities at each corner - there cannot be a unique solution.

Terminology One talks about a 'Uniqueness Rectangle' (UR) that has to be avoided. Maybe 'Nonuniqueness Rectangle' would have been more appropriate.

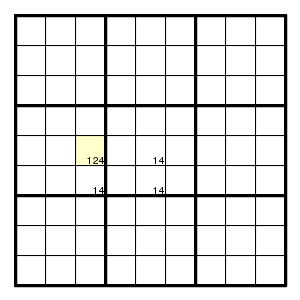
Therefore, if this last diagram is part of a puzzle with a unique solution, then the yellow cell must be 2.

That is, if three corners of such a rectangle contain the same pair of digits, then one can delete the elements of the pair from the possibilities in the fourth corner.

If two corners contain the same pair and the two other corners contain additional possibilities, then one can use that at least one of these other possibilities must actually happen. For example, in

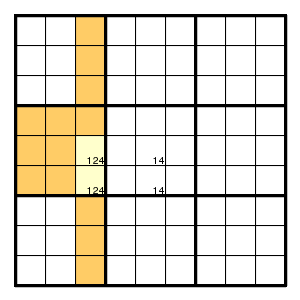
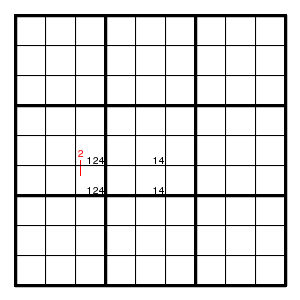
one of the two yellow squares must contain a 2, and therefore none of the orange squares can contain a 2. In other words, the uniqueness argument gives a pair here.

Another example, with the extra stuff in more corners:

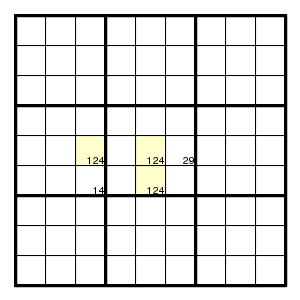
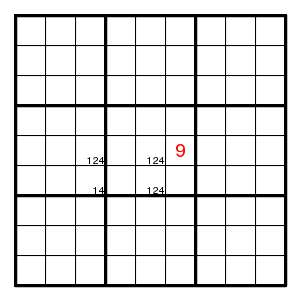
At least one of the corners is 2, so (5,6) is 9.

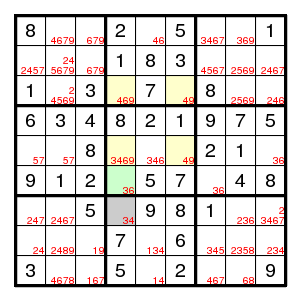
A Uniqueness Rectangle as element of a locked set

Here an example given by tso. It is very difficult without the uniqueness argument, and very easy with.

The yellow rectangle implies by uniqueness that there is a 3 or a 6 in one of the positions (3,4) and (5,4). And the other occurrence of 3,6 must be in (6,4). But then (7,4) cannot be 3 and must be 4.

Or, by a different argument (not using the pair 36 in the green square) but with the same conclusion: the only 9's in column 4 are those in the yellow rectangle. Hence neither of the yellow squares in column 4 can be 4 (by the Uniqueness Argument), so that the 4 must be in the grey square.

A Uniqueness Rectangle with pairs

This last argument concerned the case where the two sides on one corner of the rectangle are pairs for one of the two digits at the opposite corner. In that case the other digit can be eliminated. For example,

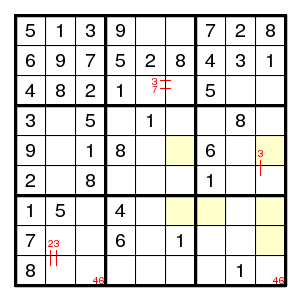
The finned X-wing for digit 2: (8,9)-(5,9)=(5,6)-(7,6)=(7,[79])-(8,9) shows that (8,9)!2, and then it follows that in row 8 the digits 2,3,8 must be on the 3 positions 2,5,7, so that nothing else is there.

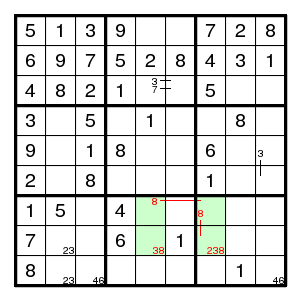
Now look at the green rectangle. If (7,7)3, then (7,5)8 and (8,7)8 so that (8,5)3 and we have a forbidden rectangle with pattern 83-38. So, (7,7)!3, which means that we have an X-wing: digit 3 in columns 2,7 can only be in rows 8,9 and does not occur elsewhere in these rows - in particular (9,4)!3 so that (6,4)3, and now all follows by singles only.

Nonunique puzzles

People wondered what happens with puzzles that do not have a unique solution. Would it be possible that using this uniqueness argument a unique solution is found?

The situation is like this: Every application of the above uniqueness argument discards an even number of solutions. So, if the puzzle has an even number of solutions, one will never find a unique solution using the above uniqueness argument. On the other hand, if the number of solutions is odd, one can pick any of the solutions and arrive at that solution after using the above uniqueness argument a number of times.

Proof Indeed, pick any two solutions A and B. The places where they differ, provided with the A-value and the B-value as candidates, forms a set of positions as required in the hypothesis of the Uniqueness Argument. This allows one to assume that at least one position in this set of positions is filled with a value that differs from the values that A and B have there. This assumption will rule out an even number of solutions, including A and B. If one wants to arrive at a given solution X, pick A, B different from X. That will do, unless X is in the set that is ruled out, that is, unless at all positions X equals A or B. But if that happens pick A and B' instead of A and B, where B' is the image of X under the involution that interchanges A-values and B-values. We need a position where X differs from both A and B'. But if X differs from A at some place, then X equals B there, so B' equals A there, so X also differs from B'. QED

(Of course one can imagine uniqueness arguments different from the above one. They might imply anything when applied to a non-unique situation.)

Prev Up Next