Start solving, and as soon as one doesn't know how to proceed, copy the entire puzzle to a new sheet of paper, and guess the value of an open square on the new sheet. Now solve the new sheet. (This might involve further sheets and guesses.) If a contradiction is found, the guess was wrong - go back to the original sheet and remove the guessed value from the set of possibilities.
This approach is fairly efficient, especially on very difficult puzzles, no time wasted with thinking.
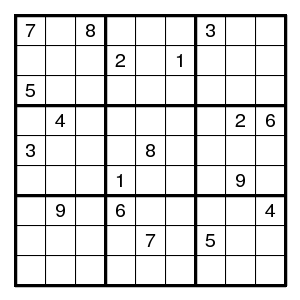
Let us do an explicit example, and solve what some have called the "most difficult Sudoku".


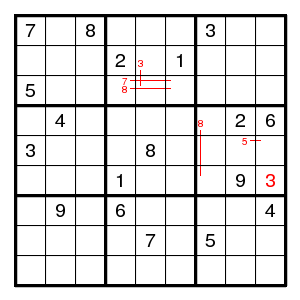
It really disappoints: we can immediately find several pairs and even a plain digit. Not *that* difficult. But then we are stuck. So let us guess, at a place where there are not that many possibilities. Since I know the solution, I can make sure that we always make the wrong guess first. Let us guess that the 3 in the middle top box is at (2,5).
Now position (2,2) can only be 6, there is a double pair 5, 8 in the top right box, and that determines the 7 there. Now in column 7 there is a double pair 6, 9, and that determines the 2 there. Also in column 2 there is a double pair 5, 7. After this things are easy: there is only one place for 8 and 3 in column 2, positions (7,1) and (7,5) are determined, we find a 1 in box 8 and a 2 in column 5.
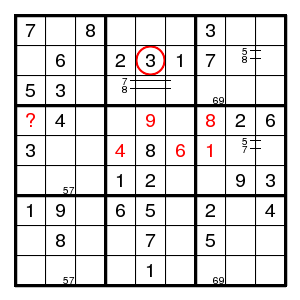
Positions (4,5), (5,4), (5,6), (5,7), (4,7) are determined. But now there is no choice for (4,1). We guessed wrong.
So, go back to our original situation. We now know that the 3 has to be at (3,5).
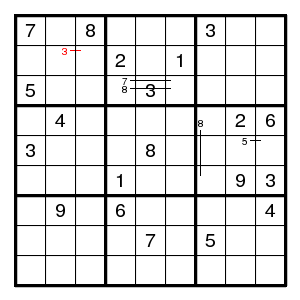
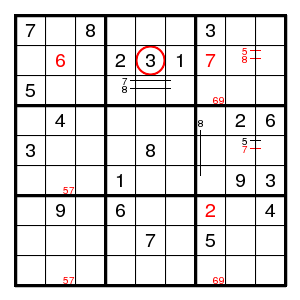
But nothing of interest seems to follow. Another guess. Let us guess that 8 is at (6,7).
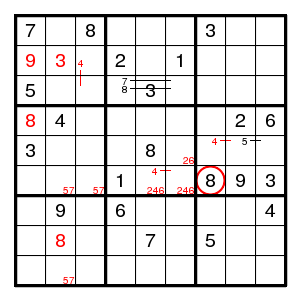
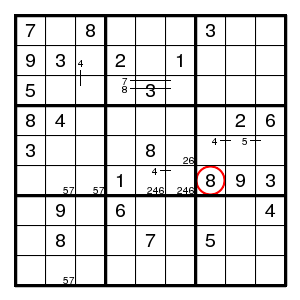
We find (4,1)8, (2,1)9, encounter a 3-set 246 in box 5, a double pair 57 in row 6 and in column 2, then (8,2)8 and (2,2)3. But what next? One more guess. Let us guess that 4 is at (2,3).
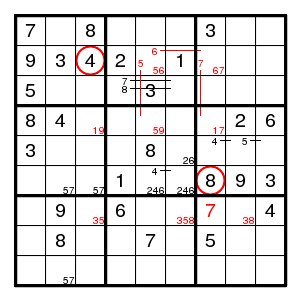
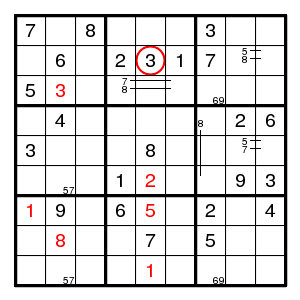
Still not easy to make progress. The forcing cycle (2,5)5 > (4,5)9 > (4,3)1 > (4,7)7 > (2,7)6 > (2,5)5 shows that there is a pair for 6 on row 2 and a pair for 5 in column 5 and a pair for 7 in column 7. There is a 3-set 358 in row 7, and we find (7,7)7 in row 7, contradicting the pair just found. So we guessed wrong and 4 is at (3,3).
Remark Note the use of a cycle that does not yield a contradiction to force pairs!
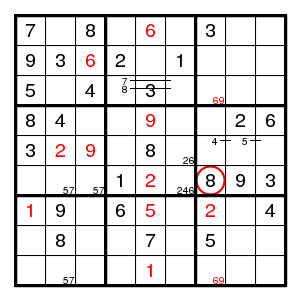
We find (2,3)6, a double pair 69 in column 7, (7,7)2, (7,1)1, (7,5)5, (9,5)1, (1,5)6, (4,5)9, (5,3)9, (5,2)2, leaving no place for 2 in box 1. So we guessed wrong and 8 is at (4,7).
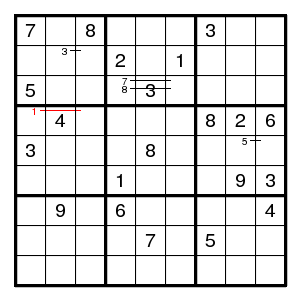
Once more we have to guess. Let us guess (4,3)1.
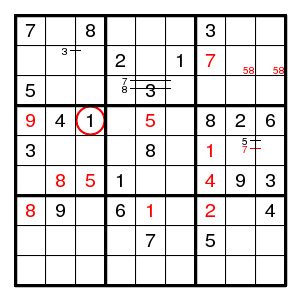
We find (4,1)9, (4,5)5, a double pair 58 in row 2, (2,7)7, (6,7)4, (5,7)1, (7,7)2, (7,5)1, (7,1)8, (6,2)8, (6,3)5, and there is no room for a 7 in box 4 anymore. So we guessed wrong and 1 is at (4,1).
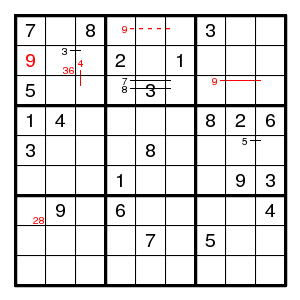
We find (2,1)9. And that is about it. Have to guess again.
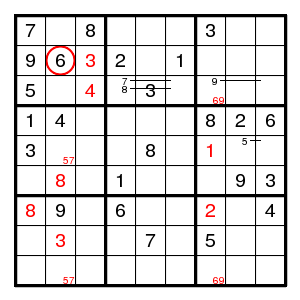
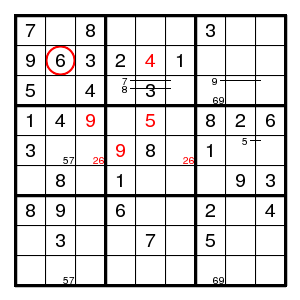
We find (2,3)3, (3,3)4, a double pair 69 in column 7, (7,7)2, (5,7)1, (7,1)8, (6,2)8, a double pair 57 in column 2, (8,2)3, and then a double pair 26 in row 5, (4,3)9, (4,5)5, (2,5)4, (5,4)9. Now the only place for 4 in column 7 is (7,7) while the only place for 4 in row 5 is (5,8), and these are both in box 6. Contradiction. So we guessed wrong and (2,2) has 3.
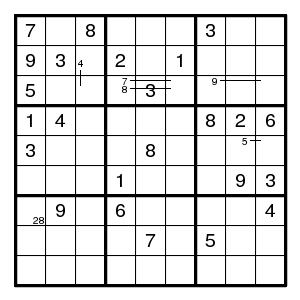
Unfortunately, there is still nothing obvious. Yet another guess. Let us guess (3,3)4.
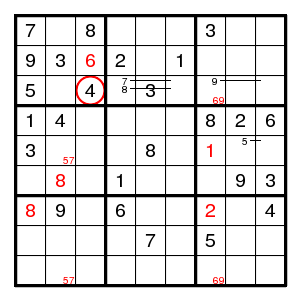
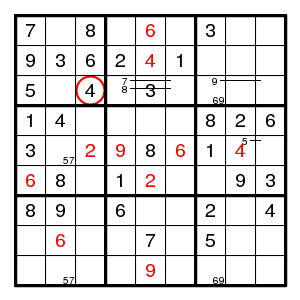
We find (2,3)6, a double pair 69 in column 7, (7,7)2, (5,7)1, (7,1)8, (6,2)8, a double pair 57 in column 2, all very familiar. Next (6,1)6, (5,6)6, (8,2)6, (1,5)6, (5,3)2, (5,4)9, (9,5)9, (6,5)2, (2,5)4, (5,8)4, and there is no place for a 4 in column 7. So we guessed wrong and this 4 is at (2,3).
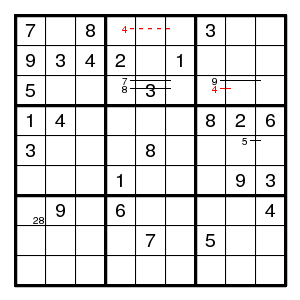
Still no progress. Maybe this was a difficult puzzle. Let us guess (7,1)8.
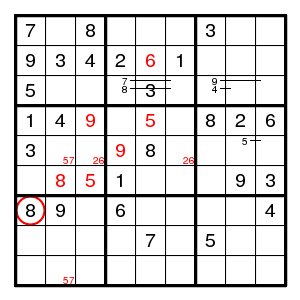
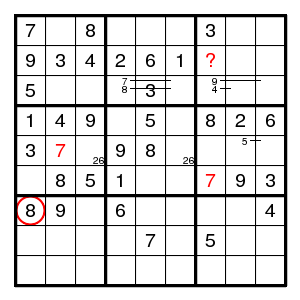
We find (6,2)8, a double pair 57 in column 2, a double pair 26 in row 5, (4,3)9, (5,4)9, (4,5)5, (2,5)6, (6,3)5, and then (5,2)7, (6,7)7. But now there is no possible value for (2,7). So we guessed wrong and (7,1) was 2.
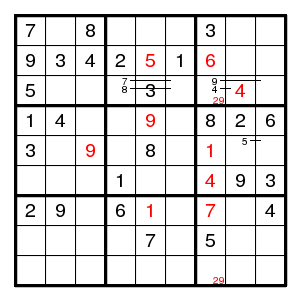
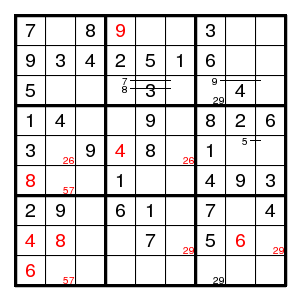
We find a double pair 29 in column 7, (3,8)4, (2,7)6, (2,5)5, (4,5)9, (7,5)1, (7,7)7, (5,7)1, (6,7)4, (5,3)9, and then a double pair 26 in row 5, (5,4)4, (1,4)9, a double pair 29 in row 8, (8,1)4, a double pair 57 in column 2, (6,1)8, (8,2)8, (9,1)6, (8,8)6, and then
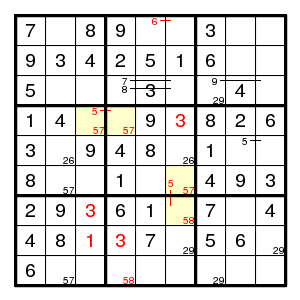
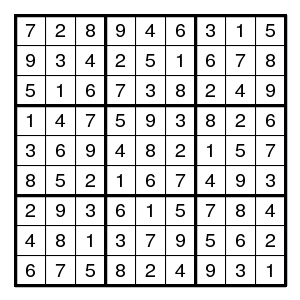
(8,4)3, (4,6)3, (8,3)1, a double pair 57 in boxes 4 and 5, two pairs 58 in box 8, and then (7,3)3 is forced by the TurbotFish (for 5) on the yellow positions. The rest is completely uneventful.