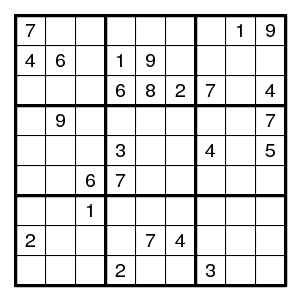
The bivalue forcing chains generalized this to a one-sided implication: if one vertex of the link has d and a neighbour has the two possibilities de, then it must be e. (But perhaps not conversely.)
The alternating pair chains form a different generalization: here the vertices may have many possibilities, but the links are alternatingly pairs (for some digit d that is constant along the chain) or ordinary adjacencies. Here the information that is pushed along the chain alternates: d - not-d. The chain works in both directions.
The common generalization of these is a chain with elements either (i,j)d or (i,j)!d (meaning: the digit at position (i,j) is d, resp. is not d), and the rules are such that each element of the chain implies the next element. As always, if a contradiction is seen, the first element of the chain is false.


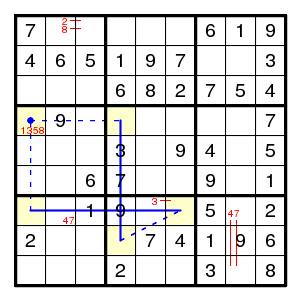
The TurbotFish (4,4)=(8,4)-(7,6)=(7,1) for the digit 8 shows that (4,1) is not 8. (In fact also (8,4)=(7,6) is a pair, but we do not need that.) However, this doesn't help at all, a more complicated chain is needed.
The forcing chain
(1,4)5 > (4,4)4 > (4,3)!4 > (9,3)4 > (9,1)9 > (7,1)6 > (7,6)8 > (8,4)5 > (1,4)!5
shows that (1,4) is not 5. The reasons for each step can be described more explicitly:
(1,4)5 =4= (4,4)4 > (4,3)!4 =4= (9,3)4 =9= (9,1)9 =6= (7,1)6 =8= (7,6)8 > (8,4)5 > (1,4)!5.
Here the earlier pair notation = is annotated with the digit involved: (1,4)=(4,4) is a pair for the digit 4, noted (1,4)=4=(4,4), and hence if (1,4) is not 4, then (4,4) is 4. The step (4,4)4 > (4,3)!4 just says that if (4,4) is 4, then a neighbour is not 4. The step (7,6)8 > (8,4)5 is for a position (8,4) that has only the two possibilities 5,8. (No attempt was made to show the nature of the links in the diagram.)
This forcing chain gives a digit 4, then a pair 58 in the middle box.
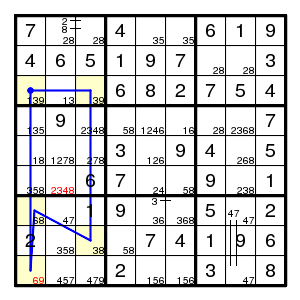
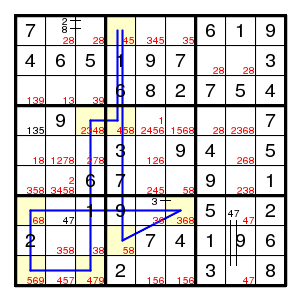
The next step is another TurbotFish: (4,1)=(4,4)-(8,4)=(8,2) for the digit 5. This time it eliminates two values: neither of (6,2) and (9,1) is 5, and the latter is what is needed.
We have enough bivalued fields now for a bivalue forcing chain:
(3,1)9 > (3,3)3 > (8,3)8 > (7,1)6 > (9,1)9 > (3,1)!9
showing that (3,1) is not 9 (and hence (3,3) is 9). After this things go smoothly, until
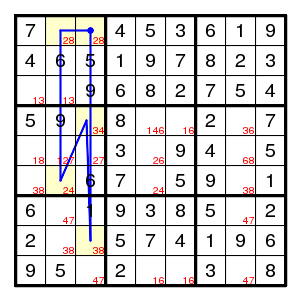
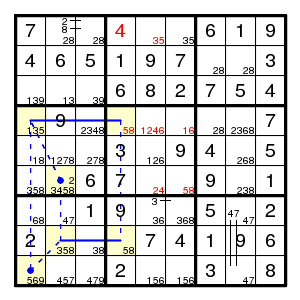
where another bivalue forcing chain helps:
(1,3)8 > (8,3)3 > (4,3)4 > (6,2)2 > (1,2)8 > (1,3)2
so that (1,3) is 2. Now all is straightforward.