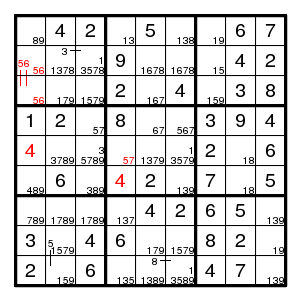



After a bit of work, the puzzle shown is brought to this state here. Now the solution is the forcing chain (5,4)!5 > (9,4)5 > (8,569)179 > (7,4)!7 > (5,4)7 that shows that (5,4) must have 5 or 7, eliminating the other three candidates.
Here the notation (8,569)179 means that the three positions (8,5), (8,6), (8,9) contain the three values 1, 7, 9 in some unspecified order.
Afterwards things are straightforward: we find a 4 in box 5, a 4 in box 4, a double pair 56 in column 1, and then singles suffice.