Prev Up Next

Advanced colouring

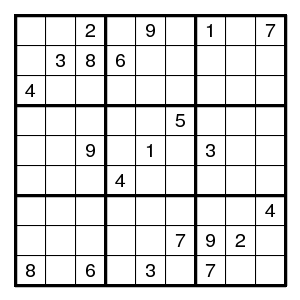
The following puzzle was posed by Jeff and discussed by Lummox JR.

Easy steps only give three double pairs, and then more is needed.

Swordfish

The next step is a swordfish: the digit 4 in columns 3,5,7 can only be in rows 2,4,8, so does not occur elsewhere in these rows.

Colouring

Lummox JR proposes to do colouring for all digits. Since that requires too many colours to work with, designate the colours by letters, where upper and lower case denote what earlier were the darker and lighter shades: two possibilities of which precisely one must be correct.

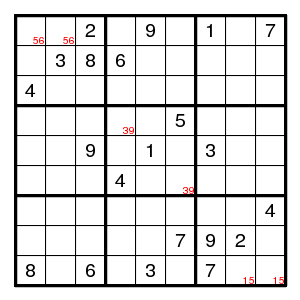
In the grid below we repeat the possibilities just found, and write letters below some of the possibilities. (Which? Each time there is a bivalue, like the 56 in (1,1) and each time there is a pair, like the 4 in row 1 that must be in either (1,6) or (1,8), it is designated by a new upper/lower case letter, unless some element of the pair has a letter already. We find 17 colours. Each colour except c/C touches two cells only.) 

56
aA
 
56
Aa
 2 
38
bB
 9 
348
 c 
 1 
348
 C 
 7 
179
def
 3 8 6 
2457
 C E
 
12
Dd
 
245
 c 
 
59
gG
 
259
4 
179
  F
 
17
hH
 
123578
    i 
 
2578
 
1238
 
2568
 
35689
 
235689
 j    
 
12367
 
12678
 
1347
  c 
 
39
kK
 
2678
 5 
2468
 C  
 
16789
 
12689
 
2567
 
245678
 C    
 9 
278
 I 
 1 
268
 l 
 3 
45678
c    
 
2568
 
123567
 
125678
 
1357
 4 
2678
 
39
Kk
 
2568
 
156789
 
125689
 
123579
     F
 
12579
 
1357
 
12589
 
2568
 
12689
  L  
 
68
mM
 
368
j  
 4 
135
 
15
nN
 
1345
  C 
 
158
 
4568
c o 
 7 9 2 
368
JO 
8 
249
 c 
 6 
29
pP
 3 
249
 C 
 7 
15
qQ
 
15
Qq

Now we must decide which pairs of colours exclude each other. Each time several letters occur as alternatives in the same cell at most one can be true. This holds for def, CE, co, JO. And each time several letters that denote the same digit occur together in the same row, column or box, at most one can be true. This holds for fG (row 2), Hi (row 3), Lm (row 7), AN (col 2), bk, KP (col 4), gQ (col 8), dh, eH (box 1), Ei (box 2), Lo (box 8), mO (box 9).

More exclusions can be generated by the rule: if x excludes z and y excludes Z and (at least) one of z and Z is true, then x excludes y.

But maybe it is easier to work with implications instead of exclusions, since there is a transitivity in implications. And y excludes Z is the same as y implies z (and as Z implies Y).

What we have so far: 

d -> F and f -> D
d -> H -> E -> c -> O -> j and J -> o -> C -> e -> h -> D
i -> e -> F and f -> E -> I
f -> g -> q and Q -> G -> F
L -> O -> M and m -> o -> l
b -> K -> p and P -> k -> B
A -> n and N -> a
There are no contradictions here, so all colours are possible. Next look at the fields that did not get a letter and look for conflicts.

We have (5,1)7 > E,i > I,i, impossible. So (5,1)!7. Of course this is the Turbot Fish for the digit 7: (5,1)-(2,1)=(2,5)-(3,4)=(5,4)-(5,1).

We have (5,9)6 > L,o > L,l, impossible. So (5,9)!6. Of course this is the Turbot Fish for the digit 6: (5,9)-(5,6)=(7,6)-(8,5)=(8,9)-(5,9).

We have (1,8)3 > c,B,J > j,J, impossible. So (1,8)!3. (That saved finding a longish forcing chain.) Now there are only two possible 3's on row 1, and we can label (1,6)3 with B, and add the implications B > C and c > b. In box 3, digit 3 must be in row 3, so it does not occur elsewhere in row 3.

We have (9,6)2 > c,P,D > c,C, impossible. So (9,6)!2. Now (9,6) has become bivalued, and we can label (9,6)9 with c.

We have (7,4)9 > f,k,p,C > f,F, impossible. So (7,4)!9. Now there are only two possible 9's in column 4, and we can put K=p, k=P.

We have (7,6)9 > f,K,p,C > f,F, impossible. So (7,6)!9. Now there are only two possible 9's in box 8, and we can put c=p, C=P, and it follows that also b=c, B=C. Row 1 now shows that we can label (1,6)3 with C and (1,8)8 with c. In box 8, digit 9 must be in row 9, so it does not occur elsewhere in row 9, that is, (9,2)!9. In column 6, the digits 3,4,9 must be in rows 1,6,9, so no other digits are there, that is, (1,6)!8.

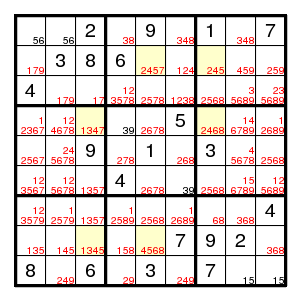
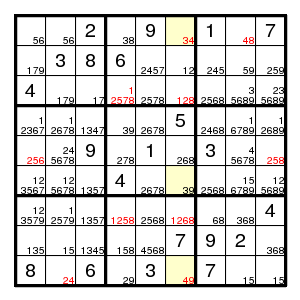
Let us make a new diagram showing the current state of affairs. So far, we have eliminated 10 possibilities. 

56
aA
 
56
Aa
 2 
38
cC
 9 
34
Cc
 1 
48
Cc
 7 
179
def
 3 8 6 
2457
 C E
 
12
Dd
 
245
 c 
 
59
gG
 
259
4 
179
  F
 
17
hH
 
12578
   i 
 
2578
 
128
 
2568
 
35689
J    
 
235689
 j    
 
12367
 
12678
 
1347
  c 
 
39
Cc
 
2678
 5 
2468
 C  
 
16789
 
12689
 
256
 
245678
 C    
 9 
278
 I 
 1 
268
 l 
 3 
45678
c    
 
258
 
123567
 
125678
 
1357
 4 
2678
 
39
cC
 
2568
 
156789
 
125689
 
123579
     F
 
12579
    f
 
1357
 
1258
 
2568
 
1268
  L 
 
68
mM
 
368
j  
 4 
135
 
15
nN
 
1345
  C 
 
158
 
4568
c o 
 7 9 2 
368
JO 
8 
24
Cc
 6 
29
cC
 3 
49
Cc
 7 
15
qQ
 
15
Qq
 

d -> F and f -> D
d -> H -> E -> c -> O -> j and J -> o -> C -> e -> h -> D
i -> e -> F and f -> E -> I
f -> g -> q and Q -> G -> F
L -> O -> M and m -> o -> l
A -> n and N -> a

We have (4,3)3 > C,c, impossible. So (4,3)!3. Now there are only two possible 3's in row 4, and we can label (4,1)3 with c.

We have (4,3)1 > C,H > h,H, impossible. So (4,3)!1. Now (4,3) has become bivalued, and we can label (4,3)7 with C.

We have (3,9)9 > f,J > f,F, impossible. So (3,9)!9. Now there are only two possible 9's in row 3, and we can label (3,8)9 with f.

We have (7,1)3 > f,J > f,F, impossible. So (7,1)!3. Now there are only two possible 3's in row 7, and we can label (7,3)3 with J.

We have (4,1)7 > C,E > e,E, impossible. So (4,1)!7.

We have (4,7)8 > c,m > M,m, impossible. So (4,7)!8.

We have (7,4)8 > c,m > M,m, impossible. So (7,4)!8.

That were seven more eliminations, but that was all, and the present approach does not help any further. The current state, as also found by Lummox JR is

WXYZ-wing

However, Jeff reports that there still is a wxyz-wing. And indeed, each of the four possibilities of the green cell eliminate the possibility 1 for the red cell. Hence (8,3)!1.

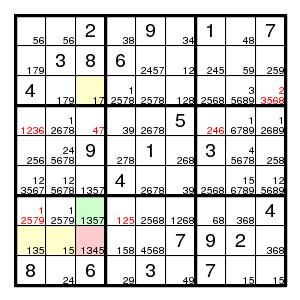
That is all progress reported in the thread referred to. What next?

Almost locked sets

Study the same neighbourhood where this wxyz-wing worked. On the cells (8,1) and (8,2) and one of (7,3),(8,3),(8,4) we have an almost locked set for the three digits 1,3,5. So, let us give names to the three cases (7,3)7, (8,3)4, (8,4)8. When one of these is false there is a strong conclusion.

Label (7,3)7 with r, and (8,4)8 with t, so that r > c,h,j and t > c. Then R = (7,3)!7 > (8,1;8,2;7,3)135 > (8,3)4 = C, so that r = c and R = C. But now both c > h and C > h, which means that h and D hold and H and d are false. Also T = (8,4)!8 > (8,124)135 > (8,9)!3 = j, but also t > c > j, which means that j holds and J is false.

More colouring

Let us redraw the grid, adding a colour s/S for (8,1)3 and (8,3)3, and a colour u/U for (7,4)1 and (8,4)1, and a colour v/V for (3,6). We see that M=O. 

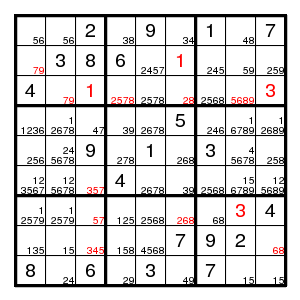
56
aA
 
56
Aa
 2 
38
cC
 9 
34
Cc
 1 
48
Cc
 7 
79
ef
 3 8 6 
2457
 C E
 1 
245
 c 
 
59
gG
 
259
4 
79
EF
 1 
2578
  i 
 
2578
 
28
vV
 
2568
 
5689
   f
 3 
1236
  c 
 
12678
 
47
cC
 
39
Cc
 
2678
 5 
246
 C 
 
16789
 
12689
 
256
 
245678
 C    
 9 
278
 I 
 1 
268
 l 
 3 
45678
c    
 
258
 
123567
 
125678
 
357
s  
 4 
2678
 
39
cC
 
2568
 
156789
 
125689
 
12579
    F
 
12579
    f
 
57
Cc
 
125
u  
 
2568
 
268
 L 
 
68
mM
 3 4 
135
 s 
 
15
nN
 
345
SC 
 
158
U t
 
4568
c m 
 7 9 2 
68
Mm
8 
24
Cc
 6 
29
cC
 3 
49
Cc
 7 
15
qQ
 
15
Qq

Now C > s because of (8,3) and s > C because of row 6. Hence C = s and S = c. It follows that (6,1)!3 and (8,3)!5. Now there are two possible 5's in column 3, and we can label (6,3)5 with c. Clearly (6,3)!7. Implications: 

E -> c -> O and o -> C -> e
i -> e -> F and f -> E -> I
f -> g -> q and Q -> G -> F
L -> M and m -> l
A -> n -> u and U -> N -> a
C -> n and N -> c
t -> c = S and s = C -> T
t -> u and U -> T
V -> c and C -> v

We have (7,4)2 > U,C > N,n, impossible, so (7,4)!2. Now label (7,4)5 with U.

We have (5,2)5 > c,C, impossible, so (5,2)!5.

We have (3,4)2 > I,V,C > V,v, impossible, so (3,4)!2.

We have (7,6)2 > l,V,C > V,v, impossible, so (7,6)!2. Now (7,6) and (7,7) form a double pair for 6,8, so L=M and l=m.

Now (7,5)!68. Introduce a new colour w/W for (7,5). Then w > C.

We have (2,5)5 > w,c,e > C,c, impossible. So (2,5)!5.

Now digit 5 occurs in box 2 in row 3, so (3,7)!5. Introduce a new colour x/X for (3,4)5 and (3,5)5. Introduce a new colour y/Y for (2,7)5 and (6,7)5. 

56
aA
 
56
Aa
 2 
38
cC
 9 
34
Cc
 1 
48
Cc
 7 
79
ef
 3 8 6 
247
 CE
 1 
245
 cy
 
59
gG
 
259
4 
79
EF
 1 
578
xi 
 
2578
 X  
 
28
vV
 
268
 
689
  f
 3 
1236
  c 
 
12678
 
47
cC
 
39
Cc
 
2678
 5 
246
 C 
 
16789
 
12689
 
256
 
24678
 C   
 9 
278
CI 
 1 
268
 m 
 3 
45678
c    
 
258
 
12567
 
125678
 
35
Cc
 4 
2678
 
39
cC
 
2568
 Y  
 
156789
 
125689
 
12579
    F
 
12579
    f
 
57
Cc
 
15
uU
 
25
wW
 
68
Mm
 
68
mM
 3 4 
135
 C 
 
15
nN
 
34
cC
 
158
U t
 
4568
c m 
 7 9 2 
68
Mm
8 
24
Cc
 6 
29
cC
 3 
49
Cc
 7 
15
qQ
 
15
Qq
 

E -> c -> O and o -> C -> e
i -> e -> F and f -> E -> I
f -> g -> q and Q -> G -> F
A -> n -> u and U -> N -> a
C -> n,w and N,W -> c
t -> c,u,M and C,U,m -> T
V -> c -> W -> x -> I,u and i,U -> X -> w -> C -> v

Now y > C and Y > C. But that means that C holds and c is false. And from C we also get e,F,n,u. That solves everything. We find 

56
 
56
 2 8 9 3 1 4 7
7 3 8 6 4 1 
25
 
59
 
259
4 9 1 7 5 2 
68
 
68
 3 
12
 
68
 7 3 
68
 5 4 
19
 
129
 
56
 4 9 2 1 
68
 3 7 
58
 
12
 
58
 3 4 7 9 
25
 
68
 
12568
9 7 5 1 2 
68
 
68
 3 4
3 1 4 5 
68
 7 9 2 
68
8 2 6 9 3 4 7 
15
 
15

The puzzle is completed by simple colouring for the digit 8 (or a Turbot Fish for 8: (5,9)-(5,6)=(4,5)-(8,5)=(8,9)-(5,9)). We see that (5,9)!8, and the rest is singles.

Prev Up Next