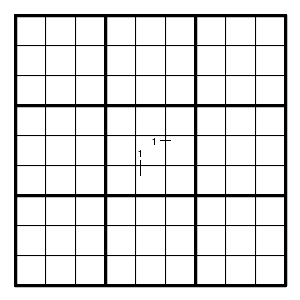
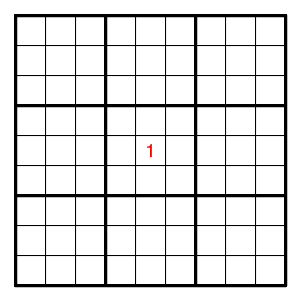


since one box cannot have two 1's.
Or again, with two intersecting pairs for the same digit, but not in a single box:
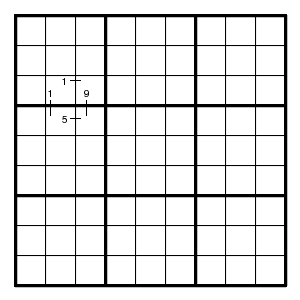
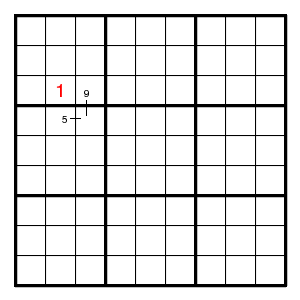
since otherwise two different values are forced for the point opposite to the point of intersection.
For example, suppose all possible positions for digit 3 in rows 2 and 5 are as shown.
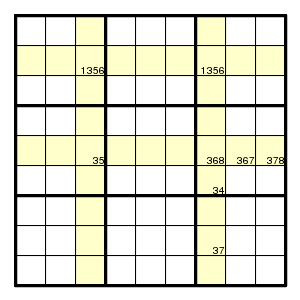
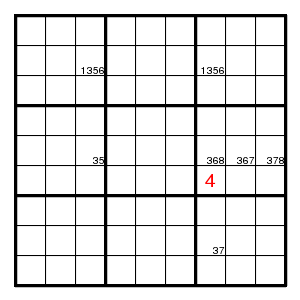
Then position (6,7) cannot be 3, otherwise also position (5,3) would be 3, and moreover one of positions (2,3) and (2,7), so that columns 3 and 7 would have three digits 3.
Terminology People call this 'X-wing with fin' ('finned X-wing').
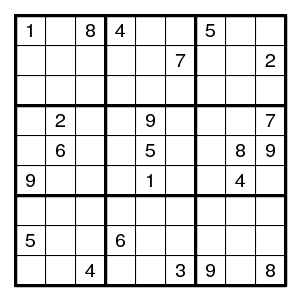
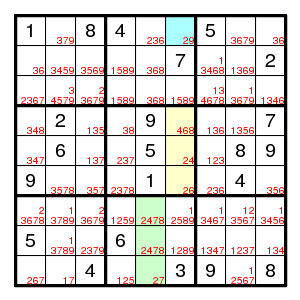
After some work, the puzzle shown has proceeded to the given stage, and the usual methods make no progress. Now look at the yellow cells. They form an almost locked set, and if (1,6)2 then they form a locked set and must have the digits 4,6,8. Then in the middle bottom box digits 4,7,8 must fill the middle column. But also the digit 2 must be there, since it cannot be in the middle top box if (1,6)2. Hence (1,6)!2, that is, (1,6)9.
Consider the following diagram, where only the candidates for digit 8 are indicated (with a # mark). The goal is to conclude that position (1,1) cannot have an 8.
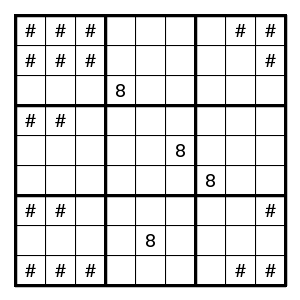
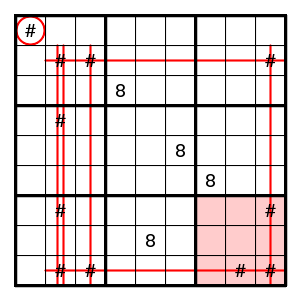
One way to proceed is to assume that (1,1) has an 8, and to count how many digits 8 are seen in the seven areas indicated (four columns, two rows and one box). Since each of these areas should contain a unique digit 8, the total should be 7. Now each # mark is covered by at least two of these areas, so is counted at least twice, and that means that there is room for at most 3.5 digits 8 where we need 4. Therefore position (1,1) does not have an 8.
(In this case one can also follow the chain: if (1,1), then also (4,2), then also (7,9), then also (2,3), then no further choice is possible.)