Prev Up Next

Digit patterns and jigsaw puzzles

For a given digit, there are 9.6.3.6.4.2.3.2.1 = 66 = 46656 possible patterns. When a partial grid has been given, the number of possible patterns is much smaller. For example, in the example used to illustrate backtrack, the numbers of patterns consistent with the givens is 
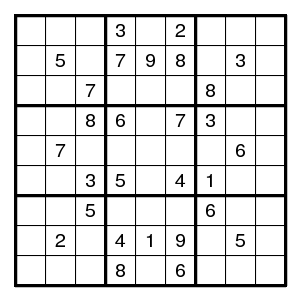
1: 88 patterns
2: 43 patterns
3: 62 patterns
4: 92 patterns
5: 62 patterns
6: 107 patterns
7: 70 patterns
8: 43 patterns
9: 48 patterns
Now one can turn a Sudoku puzzle into a jigsaw puzzle: make pieces for all possible digit patterns, and find one piece for each digit such that these pieces fit together and form the 9x9 grid.

Note that generating all possible patterns for each digit involves nine backtrack searches.

Backtrack and fun

There is debate on the rules of the game. If all one wants is the solution for some Sudoku puzzle, then one can feed it to a computer and obtain the answer in a fraction of a millisecond. Without a computer one can employ backtrack if needed and obtain the answer within an hour. But maybe that is no fun. The fun part is to apply logical reasoning to find out where the digits should go, and to avoid boring, mechanical work. The "digit pattern approach" is not really about solving Sudokus, it is about solving POM puzzles. One starts with a Sudoku puzzle, does some boring, mechanical work to find all possible digit patterns, and then has an interesting puzzle: given these jigsaw pieces, how to select pieces that fit together.

Example

This example was given by Myth Jellies, the inventor of the POM (Pattern Overlay Method, that is, jigsaw) technique. Consider the Sudoku

The numbers of possible patterns are smaller than in the example above (because there are more givens) but is still a bit large: 

1: 32 patterns
2: 28 patterns
3: 9 patterns
4: 90 patterns
5: 3 patterns
6: 9 patterns
7: 12 patterns
8: 5 patterns
9: 16 patterns
Do first some easy work, to get to

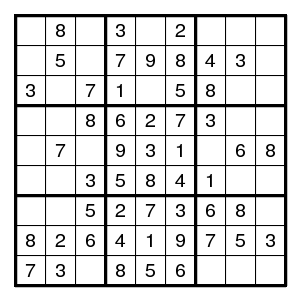
And now: 

1: 7 patterns
2: 6 patterns
3: 1 pattern
4: 7 patterns
5: 2 patterns
6: 4 patterns
7: 2 patterns
8: 1 pattern
9: 10 patterns
That looks manageable, 40 jigsaw pieces. How to represent them? Myth Jellies proposes the notation where the jigsaw pieces are named 1a,1b,...,1g,2a,...,2f,3,4a,...,9j and drawn in one grid: 

4ab 6a
 8 
1ab 4cd 9abcdefgh
 3 
4efg 6bc
 2 
5a 9ij
 
1cde 7a
 
1fg 5b 6d 7b
 
1c 2ab 6bd
 5 
1defg 2cdef
 7 9 8 4 3 
1ab 6ac
3 
4efg 6c 9ij
 7 1 
4abcd 6ad
 5 8 
2acd 9abcd
 
2bef 6b 9efgh
 
1adf 5b 9aei
 
1bceg 9bf
 8 6 2 7 3 
4acef 9ghj
 
4bdg 5a 9cd
 
2ce 4cde 5a
 7 
2ab 4abfg
 9 3 1 
2df 5b
 6 8 
2df 6c 9cgj
 
6abd 9dh
 3 5 8 4 1 
2be 7b 9efi
 
2ac 7a 9ab
 
1beg 4fg 9bdfh
 
1adf 4abcd 9aceg
 5 2 7 3 6 8 
1c 4e 9ij
8 2 6 4 1 9 7 5 3
7 3 
1c 4e 9ij
 8 5 6 
2abce 9abcdefgh
 
1abfg 2f 4bdg
 
1de 2d 4acf

The original Sudoku is a graph colouring problem. Here we have a clique-finding problem: find the unique 9-clique in the graph where compatible jigsaw pieces are joined. Two pieces are compatible when they do not overlap. (And both graph colouring and clique-finding are difficult in general.)

Vulnerable pairs

If there are two fields such that every pattern for some digit d contains at least one of those, then all patterns for other digits that cover both positions can be discarded (since they overlap every possible d-pattern). This is called a vulnerable d-pair.

In the above example, positions (6,1) and (9,7) cover all 2-patterns (that is, form a vulnerable 2-pair) and hence patterns 9c and 9g are impossible. Positions (1,7) and (4,1) form a vulnerable 5-pair, showing that 9i is impossible.

Equivalences

Use a string like 2be9f as abbreviation for the statement "precisely one of 2b and 2e and 9f holds". Of course, every string in an open grid square is such a (true) statement. Use = for the equivalence <=>. (We have now turned the problem into a satisfiability problem for the formula that is the conjunction of the statements found in the grid squares, together with the formulae 1abcdefg etc. describing that every digit has some pattern.)

Since 2abcdef and 2abce9abdefh (by (9,7)), we have 2df = 9abdefh. By (6,1) it follows that 2df6c9j, that is, 6c9abdefhj. Since 9abdefhj it follows that 6c is impossible.

Since 6abd and 6abd9dh (by (6,2)), 9d and 9h are impossible.

By (3,8) we have 2acd9ab. Now 2df = 9abef and 2bef = 9ab, so that 2df includes 2bef, and 2b and 2e are impossible, and we have 2f = 9ab and 2d = 9ef and 9j = 2ac.

From 2ac9abef and 2ac7a9ab (by (6,9)) it follows that 7a = 9ef and 7b = 2ac9ab.

From 5ab and 5b9abef (by (5,6)) it follows that 5a = 9abef and 5b = 2ac. But 1fg5b6d7b by (1,9), that is, 1fg2aacc6d9ab. By the 'precisely one' clause, this means that 2a and 2c (and 9j) are impossible. And hence 5a is the right 5-pattern.

From 4abcdefg and 4efg (by (3,2)) and 4acef (by (4,8)) and 4abfg (by (5,3)) it follows that 4f is the right 4-pattern.

From 1beg4f9bf (by (7,1)) and 1de4f9ef (by (9,9)) it follows that 1b, 1d, 1e, 1g, 9b, 9e, 9f are all impossible.

Examining what is left, we see 9a, 6a and 1c. Altogether, the solution to our puzzle is 1c, 2f, 3, 4f, 5a, 6a, 7b, 8, 9a.

Discussion

Since formula satisfiability is hard, solving such jigsaw puzzles will in general require some form of backtrack. But in the above example the simple strategy "always try to replace single elements (or short strings) by longer strings" worked successfully.

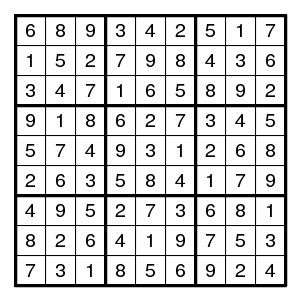
For a frightening example, see Taking on a killer Tso ... .

Prev Up Next